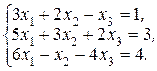Системы линейных уравнений
Рассмотрим систему m линейных уравнений с n переменными
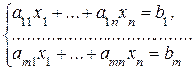
Решением системы называется набор значений переменных (с1, … , сn), при подстановке которых в систему все уравнения обращаются в верные равенства.
Система называется несовместной, если она не имеет решений.
Решить систему – значит найти множество всех ее решений.
Две системы от одних и тех же переменных называются равносильными, если любое решение каждой из этих систем является решением другой.
Система называется однородной, если все ее свободные члены равны 0. Однородная система всегда совместна, так как имеет нулевое решение.
Для решения системы используется метод Гаусса, заключающийся в последовательном исключении переменных. Для удобства систему записываем в виде матрицы (то есть прямоугольной таблицы, заключенной в круглые скобки и заполненной числами), построенной из коэффициентов и свободных членов системы. При этом столбец свободных членов отделяется от остальных столбцов вертикальной чертой. Матрица имеет вид
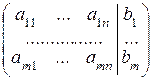
Такая матрица называется расширенной матрицей системы, а матрица из одних коэффициентов, без столбца свободных членов – основной матрицей.
Над системой допускается производить следующие элементарные преобразования, которые приводят к равносильной системе:
1) умножение какого-либо уравнения на скаляр l ¹ 0;
2) прибавление к уравнению другого уравнения, умноженного на скаляр l;
3) исключение из системы или добавление к ней уравнения с нулевыми коэффициентами и свободным членом.
Соответствующие преобразования производятся над строками матрицы системы. Преобразования приводят к эквивалентным матрицам, переходы обозначаются знаком эквивалентности ~.
Первый ненулевой коэффициент в каждой строке называем ведущим.
Цель преобразований – избавиться от переменной x1 во всех уравнениях, кроме первого. Считаем, что в первой строке ведущий элемент - a11. В противном случае поставим на первое место другую строку. Используем первую строку как опорную.
Чтобы избавиться от первого коэффициента ai1 в i-ой строке, прибавляем к этой строке первую строку, умноженную на (–ai1/a11). Проделав это со всеми строками, начиная со второй, во всех этих строках на первом месте получим 0.
Возможно, что при этом станут нулевыми все элементы не только в первом столбце, но и в нескольких следующих (без первой строки). Если же какие-нибудь ненулевые элементы в получившейся матрице останутся, то повторяем указанные преобразования с матрицей, получающейся отбрасыванием первой строки и всех столбцов до первого ненулевого.
Проделав указанные преобразования, сколько возможно, получим матрицу в ступенчатом виде. Он характеризуется тем, что ведущий элемент в каждой строке, начиная со второй, расположен правее, чем в предыдущей.
Если в последней ненулевой строке ступенчатой матрицы слева от черты стоят нули, а справа ненулевой элемент, то соответствующая система решений не имеет, то есть является несовместной.
Если такой строки в ступенчатой матрице нет, то для удобства обведем ведущие элементы во всех строках в кружки. Переменные, которым соответствуют кружки, считаются базисными, остальные – свободными. Если свободных переменных нет, то система имеет единственное решение. Для его нахождения по строкам получившейся матрицы восстанавливаем уравнения, начиная с последней, и последовательно находим значения всех переменных.
Если в системе есть свободные переменные, то придаем им произвольные значения, считая параметрами. Базисные переменные выражаются через них в том же порядке, как в предыдущем случае. Система в этом случае является неопределенной, то есть имеет больше одного решения.
Если система однородная, то в матрице столбец свободных членов не нужен, так как в этом столбце все элементы нулевые, они останутся нулевыми при любых преобразованиях.
Пример 1.1.1.Решить систему
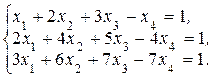
Решение. Строим матрицу системы и приводим ее к ступенчатому виду:
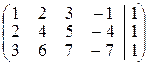 ~
~ 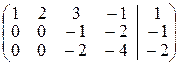 ~
~
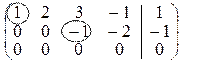
Ко второй и третьей строкам первой матрицы прибавлялась первая строка, умноженная на –2 и –3 соответственно. К третьей строке второй матрицы прибавлялась вторая строка, умноженная на –2.
Базисными являются переменные x1 и x3, свободными x2 и x4. Полагаем
x2 = a, x4 = b. Тогда из уравнения, соответствующего второй строке ступенчатой матрицы, получаем –x3 – 2b = –1, и x3 = –2b + 1. Подставляя в первое уравнение, получаем
x1 + 2a + 3(– 2b + 1) – b = 1, x1 = – 2a + 7b – 2.
Ответ: x1 = – 2a + 7b – 2, x2 = a, x3 = – 2b + 1, x4 = b, a, b Îℝ.
У п р а ж н е н и е 1.1. Решите системы:
а) 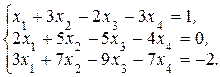
б) 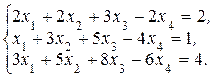
в) 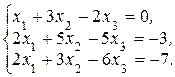
г) 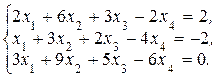
Определители
Матрица порядка m´n – это матрица с m строками и n столбцами. При m=n имеем квадратную матрицу порядка n.
Определитель квадратной матрицы порядка n – это число, которое ставится в соответствие этой матрице. Определитель матрицы заключен в прямые скобки.
Определители второго и третьего порядка вычисляются по формулам
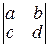 = ad – bc;
= ad – bc;
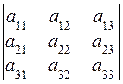 = a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a12a21a33 – a11a23a32. (1)
= a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a12a21a33 – a11a23a32. (1)
В последней формуле (1) имеем сумму произведений элементов матрицы, взятых по одному из каждой строки и каждого столбца матрицы. Часть этих произведений входит в сумму со знаком «+», остальные – со знаком «–». Чтобы правильно расставить эти знаки, можно применить правило треугольника. Произведение элементов главной диагонали матрицы (выходящей из левого верхнего угла) берется со знаком «+», и с этим же знаком берутся произведения по двум треугольникам, имеющим с этой диагональю параллельную сторону, как на левом рисунке. Произведения по второй, побочной диагонали берутся со знаком «–», как и произведения по двум треугольникам, имеющим с ней параллельную сторону (см. правый рисунок).
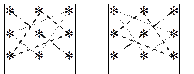
Пример 1.2.1.Вычислим определитель по формуле (1):
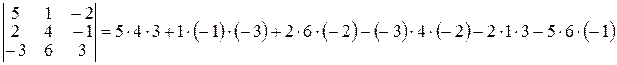 =
=
= 60 + 3 – 24 – 24 – 6 + 30 = 39.
Пример, иллюстрирующий применение определителя, это правило Крамера для решения систем n линейных уравнений с n переменными. Сначала вычисляем определитель D основной матрицы системы. Если D ¹ 0, то система имеет единственное решение. Для нахождения каждого xi вычисляем определитель Di матрицы, полученной из основной матрицы заменой i-го столбца на столбец свободных членов. Тогда xi находим по формуле xi = 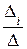 для всех i. Этот метод особенно эффективен для решения систем из двух уравнений с двумя переменными; для решения систем с большим числом уравнений и переменных удобнее метод Гаусса.
для всех i. Этот метод особенно эффективен для решения систем из двух уравнений с двумя переменными; для решения систем с большим числом уравнений и переменных удобнее метод Гаусса.
Пример 1.2.2.Решить систему 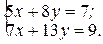
Решение. Производим вычисления:
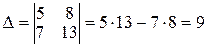 ;
;
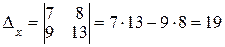 ;
; 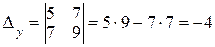 ;
;
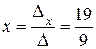 ;
; 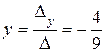 .
.
Определитель 3-го порядка можно посчитать и по другой формуле, называемой разложением по первой строке:
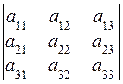 =
= 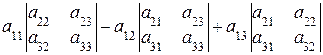 (2)
(2)
Структура формулы (2) будет ясна из следующих определений.
Минором элемента aij матрицы А (то есть элемента, стоящего и i-ой строке и j-ом столбце) называется определитель Mij(A) матрицы, полученной из А вычеркиванием i-ой строки и j-го столбца.
Алгебраическим дополнением элемента aij матрицы А называется число
Aij =(–1)i+j Mij(A).
Таким образом, формула (2) означает, что определитель получается умножением элементов первой строки на их алгебраические дополнения и суммированием полученных произведений. При применении формулы (2) не стоит выписывать определители второго порядка в правой части, их можно сразу раскрыть, мысленно выделив их в исходной матрице.
Пример 1.2.3.Вычислим определитель из примера 1.2.1 по формуле (2):
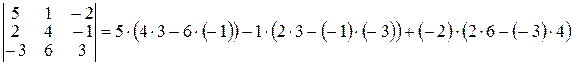 =
=
= 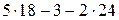 = 39.
= 39.
Для вычисления определителей более высокого порядка их порядок следует понизить. Для этого пользуются свойствами определителей:
1) если к строке (столбцу) матрицы прибавить другую строку (столбец), умноженную на произвольный скаляр, то ее определитель не изменится;
2) если строку (столбец) матрицы умножить на число l, то на l умножится ее определитель;
3) если поменять местами две строки (столбца) матрицы, то ее определитель поменяет знак;
4) определитель матрицы с нулевой строкой (столбцом) равен 0;
5) определитель матрицы А, у которой все элементы какой-либо строки (столбца), кроме, может быть, aij, равны 0, равен (–1)i+jaijMij, где Mij – определитель матрицы, полученной из А вычеркиванием i-ой строки и j-го столбца.
Для понижения порядка определителя выбираем в нем какой-нибудь элемент, обычно равный 1. Остальные элементы столбца, в котором он стоит, надо заменить нулями. Для этого используем строку, в которой стоит выбранный элемент, как опорную. Преобразуем элементы столбца в нули с помощью правила 1), как в методе Гаусса. При этом, возможно, преобразовывать придется строки не только ниже, но и выше выбранной строки. После этого понижаем порядок определителя по правилу 5). Можно, впрочем, поменять строки и столбцы ролями, делая нули не в столбце, а в строке с помощью опорного столбца.
Пример 1.2.4. Вычислить определитель
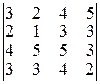 .
.
Решение. Мы имеем элемент 1 на пересечении второй строки и второго столбца. Используя вторую строку, сделаем остальные элементы во втором столбце равными 0. Для этого к первой, третьей и четвертой строкам прибавляем вторую, умноженную на –2, –5, –3 соответственно. Получаем:
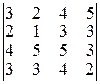 =
= 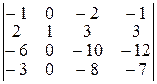 =(–1)2+2
=(–1)2+2 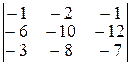 =
= 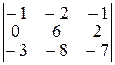 =
=
= 42 + 12 + 0 – 18 – 16 – 0 = 20.
Перед вычислением определителя третьего порядка его упростили, прибавив ко второй строке третью, умноженную на –2.
У п р а ж н е н и я
1.2.1.Решить системы по правилу Крамера:
а) 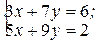 б)
б) 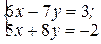 в)
в) 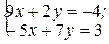 г)
г) 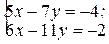
1.2.2. Вычислить определители:
а) 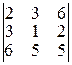 ; б)
; б) 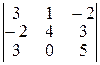 ; в)
; в) 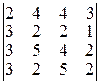 ; г)
; г) 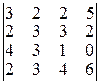 ; д)
; д) 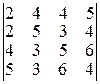 .
.
Алгебра матриц
На множестве матриц определены операции сложения, умножения на число, умножения матриц.
Складывать можно прямоугольные матрицы одного и того же порядка. Сложение выполняется поэлементно.
Умножать на число можно любую матрицу. Умножение выполняется поэлементно (то есть каждый элемент матрицы умножается на скаляр).
Пример 1.3.1.
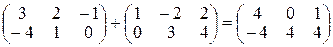 ;
; 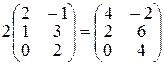 .
.
Умножать можно матрицу порядка m´k на матрицу порядка k´n, то есть длина строки первой матрицы должна быть равна длине столбца второй матрицы. В произведении получится матрица порядка m´n. Ее элемент, находящийся в i-ой строке и j-ом столбце, получается умножением элементов i-ой строки первой матрицы на соответствующие элементы j-ого столбца второй матрицы и сложением получившихся произведений.
Пример 1.3.2.
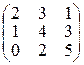
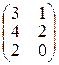 =
= 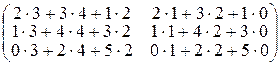 =
= 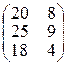 .
.
Матрицей, транспонированной к матрице А, называется матрица АТ, строки которой совпадают с соответствующими столбцами матрицы А.
Для квадратных матриц любого порядка n существует единичная матрица Е, обладающая свойством АЕ = ЕА = А для любой матрицы А. Единичная матрица имеет вид
Е = 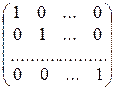 .
.
Обратной к квадратной матрице А называется матрица А-1 такая, что
А×А–1 = А–1×А = Е.
Матрицу, обратную к матрице А, существует при ïAï¹ 0. Ее можно вычислить по формуле
A–1 = ïAï–1 A*,
где A* – матрица, союзная с А. Она получается из А заменой каждого элемента его алгебраическим дополнением и последующим транспонированием.
Пример 1.3.3.Найти матрицу, обратную к
А = 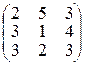 .
.
Решение. Имеем
ïAï = 6 + 18 + 60 – 9 – 16 – 45 = 14;
A* = 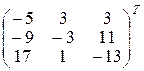 ;
;
A–1 = 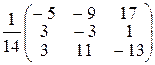 .
.
Вернемся к системе m линейных уравнений с n переменными
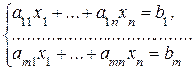 (1)
(1)
Выделим связанные с ней матрицы: основная матрица А, столбец свободных членов В и столбец переменных Х:
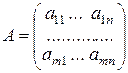 ,
, 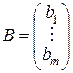 ,
, 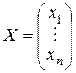 .
.
Заметим, что
АХ = 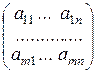
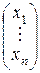 =
= 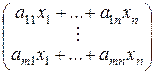 .
.
Заключаем, что это произведение матриц представляет собой матрицу из одного столбца, в котором записана левая часть системы. Правая часть – это столбец свободных членов, то есть матрица В. Значит, система может быть записана в матричном виде
АХ = В. (2)
Это очень компактная запись, но кроме этого она позволяет решать систему матричными средствами. Это возможно, если основная матрица системы А является квадратной и обратимой. Тогда, умножив уравнение (2) слева на матрицу А-1, получим Х = А-1В. Это и есть ответ, то есть столбец значений переменных.
Пример 1.1.1.Решить систему
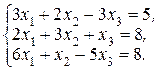
Решение. Найдем обратную к основной матрице системы А = 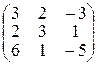 :
:
ïAï= 3(–15 – 1) – 2(–10 – 6) – 3(2 – 18) = –48 + 32 + 48 = 32;
A* = 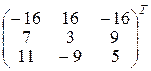 ; A–1 =
; A–1 = 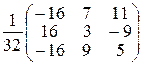 .
.
Отсюда получаем решение системы
Х = А-1В = 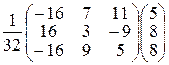 =
= 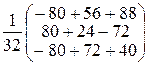 =
= 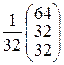 =
= 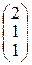 .
.
У п р а ж н е н и я
1.3.1. Выяснить, для каких матриц определены произведения, и найти эти произведения:
А = 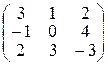 ; В =
; В = 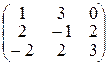 ; С =
; С = 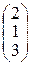 ; D =
; D = 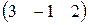 .
.
1.3.2. Найти обратную к следующей матрице:
а) 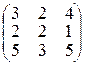 ; б)
; б) 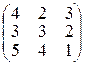 .
.
1.3.3. Решите системы тремя способами: методом Гаусса, по правилу Крамера и матричным способом:
а) 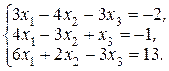 б)
б) 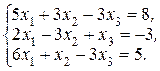 в)
в)