Тепловые воздевия на термод. с . Энтропия

Эксергия ОТС.

E^*=m(U+PV+w²/2+gh)

ΔΕ^*=Q^е-L^е

В открытой т/д сист. помимо внутр. Е дополнительными источ –ми получения работы явл.: P₁V₁ – эн. проталкивания, gh₁ – потенц.эн., w²/2 – кин. эн.

Эти источники не связаны с хоатич. формой движ–я →эти энерг.величины полностью превратимы в полез.работу.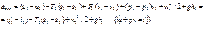

- полное выражение

Во многих задачах i₁>>gh₁, w₁²/2<<i₁→м. пренебречь.

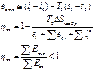
3. Ид газ –это такой газ, м/у молекулами к-го не сущ-т силового вд-я, а сами молекулы не облад ни объемом, ни массой и для к-го уравнение состояния записывается так:

pV=(m/M)RT=mŘT, где R=8,314 Дж/(моль·К), Ř=R/M

или pV =μRT, где μ=m/M

или pυ=RT/M, где υ=V/m

или pύ=RT, где ύ=V/μ

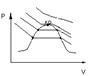
4. Реальные газы и пары. Р-V и Т-S диаграммы. Изображение основных про­цессов.

1. Уравнение Менделеева-Клайперона уже несправедливо.

2. Т/д параметры (энт-я, вн.эн.) зависит от 2- парам-в, а не только от тем-ры как для ид-го газа. u=f(P,T)

3. Тепл-сти С_р и С_v, а следовательно и показ-ль адиабатные не явл-ся пост-ми вел-ми. c_P,c_V=f(T,P)

Все рельные газы явл-ся парами тех или иных жидкостей. Причем чем ближе газ к переходу в жидкое сост-ие, тем больше его отклонение от сост-ия идеального газа.

ав- подогрев воды

вс- парообразование

сd- перегрев пара

5. Энерг.хар-ки термод. сис– мы и внеш. возд-вии на нее.

Терм. сис. – объект, кот.выбирает терм-ка – это совок-ть макротел, отдельное макротело или его часть. Энерг.хар-ки: энергия (внутр.эн.). Энергия явл мерой различных форм движения материи. Полная энергия макросистемы: E=E_кин + Е_пот +U, где U – внутр.эн. Внутр.эн. – это энергия заключенная в с/с. Она состоит из:

1) кинетич.Е поступат, вращат. и колебат.движения молекул.

2) потенциал.энерг.вд-я молекул м/у собой (силы притяж и отталкив ). Свойства внутр.эн.

U=f(T,ν) U=f(P,T) U=f(P,ν) U – функц состояния 1) ΔU= U₂ – U₁, т.е.не зависит от пути

перехода

2) 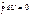свойство полного диф –ла :

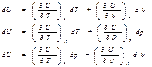
3) для ид.газа : U=f(T)

4)свойство аддетивности: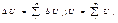

т.е.для сложной сис внутр.эн.есть сумма внутр.энергий, составляющих частей этой сис ΔU > 0, если U₂ > U₁. Энерг.внеш.возд–вие:

1) тепловое возд. – передача Е за счет хаотич –го неупор – го движ –я частиц. Такая передача Е происходит м/у телами, имеюш –ми различ-ю t-ру , либо м/у телами на расст –ии посредством эл.магн.волн. Передача Е происходит от более нагретых тел к менее нагретым. Кол – во Е при такой передаче наз.кол –вом теплоты.

2) Работа – передача Е за счет строго упоряд – го движ – я частиц. В этом сл –е передача Е происходит при перемещ всего тела или его части в простр –ве. Возд – вий в виде работы очень много. L_магн, L_вращ, L_мех и др., [Дж]. Работа, затраченная телом ‘+’, а совершенная телом ‘-’ . Ур возд – вия: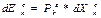

Р_к – силы (потенциалы), кот.связаны с внеш.возд. Х_к – коор –та, предт – ет собой конкр.- й пар –р, кот.изменяется соот – но этому виду возд – вия. Р_к – причины возник – я внеш.- х возд- вий. Возд – вия возникают тогда, когда есть разность сил. ΔР_к= Р^е_к – Рⁱ_к , Х^е_к – следствие возд –.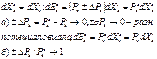

сильное неравномерное возд.→ в с/с протекаеют неравн –е процессы. 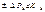- хар.степень нерав –ти.

к=2

- термодиф – формация с/с (м.б.откр.и закрытой) Число независимых пар – ров с/с (степеней свободы)= числу внеш. энерг- ких возд –вий.

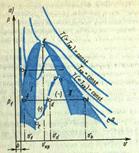
6. Реальные газы и пары. Р-V и Т-S диаграммы. Изображение основных про­цессов.

4. Уравнение Менделеева-Клайперона уже несправедливо.

5. Т/д параметры (энт-я, вн.эн.) зависит от 2- парам-в, а не только от тем-ры как для ид-го газа. u=f(P,T)

6. Тепл-сти С_р и С_v, а следовательно и показ-ль адиабатные не явл-ся пост-ми вел-ми. c_P,c_V=f(T,P)

Все рельные газы явл-ся парами тех или иных жидкостей. Причем чем ближе газ к переходу в жидкое сост-ие, тем больше его отклонение от сост-ия идеального газа.

ав- подогрев воды

вс- парообразование

сd- перегрев пара

ва - пар

g – капельная жидкость

св – пересыщенный пар

fe – перегретая жидкость

7. Та часть полного запаса Е тд-ой сист, кот не связана с пол-ем системы в поле внешних сил и с ее движением относительно тел окр ср, называетсявнутр Е тд-ой сист.

Внутр Е является функц состояния неподвиж замкнутой тд-ойсистемы и м б вычислена с пом Ур ее состояния. Значение ВЭ не зависит от того, каким обр сист достигла данного состояния. При рассмотрении открытых систем их кинетич и потенци­аль Е долж вводиться в тд-ие соотношения в виде самостоя­тельных выражений дополнительно к внутр Е

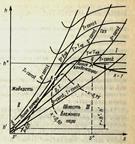
8.hs – диагр получила широкое применение, т к удобна при практических расчетах,,дает возможность вместо площадей (vp- и sT-диаграммы)измерять отрезки.

Положение пограничной кривой: для нижней (х=0)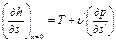

и для верхней (х=1)

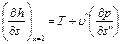
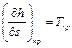Таким образом, тангенс угла наклона касательной к критической точке пограничной кривой в диаграмме равен 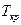. В области влажного пара в координатах s, h изобары совпадают с изотермами и представляют собой прямые линии, имеющие угол наклона, тангенс которого определяется

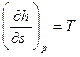. Чем выше температура, тем круче должна быть изобара.

9.Передача Е в результате макроскоп-ого упорядочен движ-яназ работой(механической или немеханической). Кол-во передаваемой при этом Е называют работой процесса.

Простейщим, наиболее наглядным видом работы является механич работа, совершаемая механической силой, кот перемещает в пространстве макроскопическое тело или некоторую его часть.

Кроме того, существуют различные виды немеханических работ. Так, электрическая работа совершается, когда некоторое количество носителей электрического заряда переносится в электрическом поле(dL_эл=-Е_элdl_эл). При совершении магнитн работы происходит организованный, соответствующий ориентации магнитного поля поворот в пространстве всех элементарных магнитов, присутствующих в намагничиваемом материале(dL_маг = -Н_магdМ_маг).

Общим для всех видов работы свойством явл-ся принципиальная возм-ть их полого количественного преобразования друг в друга.

Сумму технич работы, изменения кинетич энергии и изменения потенциальэнергии называют располагаемой работой l₀ :

l₀ = l_Т + D(w²/2) + D (gy),

или dl₀ = dl_T + d (w² /2) + gdy.

Элементарн располагаемая работа определяется произведением объема на изменение давления с обратным знаком, т.е. dl₀= - vdp.

В конечном процессе располагаемая работа находится интегрированием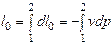

При вводе рабочего тела необх преодолевать Дей-е внутр давления в сист. Сл-но, над рабочим телом, поступающим в сист, д б совершена некот работа внешней силой, работа ввода(проталкивания), кот увеличивает полную Е сист. При выводе рабоч тела из сист ею должна затрачивать­cя работа по преодолению давления внешней среды – работавывода рабочего тела. Работа ввода- вывода равна произведению давления на объем(А_ввода=pV).

10. Сп-бы тд-их расчетов реаль газов и паров.располагаемая работа в политропном процессе в n раз больше работы расширения

.

1. Для расчета исп – тся is –диаграмма.

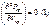
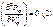
После использования (1) и (2) св-ва и ур-е Ван-дер-Ваальса

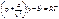
получим:

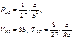
Получив из эксперимента t-ру и давл. в крит.точке, можно найти коэф. а и b:

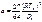
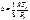
2.. Применение т/д таблиц

а) св-ва влажного нас. пара

1) таблицы по давлению;

2) таблицы по температуре.

Расчет по таблицам предпочтительнее, т.к. расчет оказывается более точным.

б) вода и перегр.пар

Р,Т=f(i,s,v)

3. Использование диф.уравнений в термодинам.

f(P,V,T)=0

Точность расчетов опред. точностью ур-й состояния.

4.Применение средств выч-й техники.

Тепловые воздевия на термод. с . Энтропия.

тепов.возд – вия -передача Е за счет хаотич –го неупор. движ –я час – ц. Такая передача Е происходит м/у телами, имеющими разл. t – ру посредством соприкоснов, либо м/у телами на рас – НИИ поср – вом эл.магн.волн. Передача Е происходит от более нагр.тел к менее нагретым. Кол – во Е при такой передаче наз.кол –вом теплоты. Все виды энергии в итоге превращаются в теплоту, кот.затем рассеив – ся в окр. среде. Мера этого рассеив –я наз.энтропией. Чем больше рассеив –ся энергия, тем больше ув –ся энтропия.Е – мера движения материи. Энтропия – мера рассеивания (деградации) энергии. S, Дж/К; s, Дж/кг*К. Свойства:

1)

ΔS_1-2 = idem изменение S не зависит от пути перемещ-я

2)

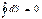диф – ал энтропии - полный диф –ал S=f(ν,Т) ; S=f(P,Т); S=f(P,ν) т.е.энтропия –функ- я некот –ых пар – ров состояния. Для случая S=f(ν,Т) :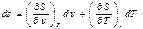

Ч/з энтр.м.выражать др.пар –ры: T=f( T,S) P=f(T,S) .

3) свойство аддетивности:

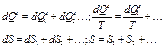
потенциал Р и Т и др. cв-вом аддет. не обладают dS>0, то dQ^e>0.

12. Дрос-ие газов и паров. Физика пр-са. Изменение т/д парам-ов. Темпе-ра инверсии

Дросселирован наз-ся процесс понижения давл в движущемся ста­ционарном потоке газа или пара при прохождении его через препятствие. Препятствия в проточных каналах встреч-ся в виде клапанов, диафрагм, вентилей, заслонок, ши­беров и т. п. Любые препятствия, встречающиеся на пути движ-я потока, в т ч и не указанные, приводят к необратимости протекающих в нем процессов, к частичной потере работосп-ти сист и, как следствие, к уменьш КПД двигателей. dh = -WdW (q=0, l_т=0, dy=0). Эксперимент показывает, что: dW=0, dh=0, т.е. h1=h2, энтальпия газа в рез-те дросселирования не изм-ся. Эффект изменения параметров при дросселировании широко исп-тся в холодильной технике для получения низких t-р, в паротехнике для получения перегретого пара. Изменение энтальпии ид газа в любых процессах связано с изменением т-ры соотношением dh = c_pdT, поэтому процесс дросселирования ид газа, для которого c_p = const, происходит без изменения температуры (dТ = 0). Температура же реальных газов в процессе дросселирования по результатам опытов может как уменьшаться, так и возрастать. В зав-ти от начальных параметров и физ-х св-в реальных газов при дросселировании значение dTм б и меньше и больше 0. Явлению дросселирования дали научное обоснование Дж. Джоуль и У. Томсон (Кельвин), вслед­ствие чего явл-е получило наименование эффекта Джоуля - Томсона. В случае неизменности т-ры при дросселировании наблюдается нулевой эффект Джоуля-Томсона. Состояние реального газа, когда дроссельный эффект равен нулю, называется точкой инверсии. В этой точке происходит смена знака температурного эффекта. Температура в этой точке называется температурой инверсии.Если температура газа перед дросселированием меньше т-ры инверсии, то газ при дросселировании охлаждается, если больше – то нагревается.