Векторы, операции над векторами. Декартов базис
Для отвлеченного изображения конкретных векторных величин используются векторы. Вектором (геометрическим) называется направленный отрезок прямой. Два вектора называются равными, если они сонаправлены и имеют одинаковую длину. Положение начальной точки таких векторов не играет никакой роли. Поэтому геометрические векторы называются свободными.
При изучении темы «Векторная алгебра» студенту следует обратить внимание на ниже рассмотренные вопросы.
1. Линейные операции над векторами (сложение, вычитание, умножение на число).
Векторы необходимо уметь складывать как по правилу треугольника, так и по правилу параллелограмма.
2. Линейная комбинация векторов. Линейная зависимость и независимость векторов. Базисные векторы. Декартов базис.
Пример 1.2.1. Указать при каких значениях α и β возможно равенство
αa + βb = 0, где а° и b° единичные векторы
(a0=a / |a|, b0=b / |b|). Для решения приведенной задачи необходимо
рассмотреть возможное расположение векторов а и b:

Рис .1.2.1 Pис .1.2.2 Рис .1.2.3
a) векторы а и bсонаправлены (Рис. 1.2.1), тогда α=-β;
b) векторы а и b имеют противоположное направление (рис.1.2.2). В этом случае α=β ;
с) векторы а и b образуют между собой угол φ. При этом угол φ отличен от 0 и π радиан (рис.1.2.3). Приведенное в условии равенство возможно лишь при α=β=0.
Рассмотренный пример дает представление о линейной зависимости и независимости векторов (важнейшее положение темы «Векторная алгебра»).

 Линейной комбинацией п векторов хi (i=1,n) называется сумма произведений этих векторов на действительные числа аi (i=1,n), а именно
Линейной комбинацией п векторов хi (i=1,n) называется сумма произведений этих векторов на действительные числа аi (i=1,n), а именно

В рассмотренном примере записана линейная комбинация 2х единичных
векторов а° и b° ) .

 Векторы хi (i=l,n) называются линейно-зависимыми, если их линейная комбинация (1.2.1) равна нулю, а среди коэффициентов ai(i=l,n) имеется хотя бы один отличный от нуля. На рис. 1. 2 .1-1. 2 . 2 изображены два линейно зависимых вектора. Они могут быть расположены на одной прямой, либо на параллельных прямых.
Векторы хi (i=l,n) называются линейно-зависимыми, если их линейная комбинация (1.2.1) равна нулю, а среди коэффициентов ai(i=l,n) имеется хотя бы один отличный от нуля. На рис. 1. 2 .1-1. 2 . 2 изображены два линейно зависимых вектора. Они могут быть расположены на одной прямой, либо на параллельных прямых.
Два вектора, расположенные на одной либо на двух параллельных прямых, называются коллинеарными.
Условие коллинеарности векторов а = λb , где λÎR. Если три вектора расположены в одной либо в параллельных
плоскостях, то они называются компланарными.
Компланарные векторы линейно зависимы. Необходимое и достаточное условие - компланарности векторов:
с = αа+βb .

 Векторы xi (i=l,n) называются линейно-независимыми, если равенство нулю их линейной комбинации (1.2.1) возможно лишь в том случае, когда коэффициенты ai(i=l, n) одновременно равны 0.
Векторы xi (i=l,n) называются линейно-независимыми, если равенство нулю их линейной комбинации (1.2.1) возможно лишь в том случае, когда коэффициенты ai(i=l, n) одновременно равны 0.
Случай двух линейно-независимых векторов представлен на
рис. 1.2.3 (линейная комбинация αа+βb равна нулю лишь при одновременном обращении в ноль α и β).
Пример 1.2.2. Векторы а,b,с некомпланарны (линейно независимы). Доказать, что векторы m=a+2b-c, п=За-b+с и р=а+5b-Зс компланарны и найти их линейную зависимость.
Приравняем к нулю линейную комбинацию векторов т,п,р (αт+ βn+γk = 0) и подставим в равенство разложения векторов т,п,р по векторам а, b,с.
α(a+ 2b- c)+β(3a- b+ c)+γ(-a+5b-3c)=(α+3β - γ)a+(2 α - β+5 γ)b+(- α+ β-3 γ)c=0
Равенство нулю линейной комбинации векторов а,b,с возможно лишь в том случае, когда коэффициенты линейной комбинации равны нулю. Из этого условия получаем систему линейных алгебраических уравнений, которую решим методом Гаусса (пример 1.1.11).
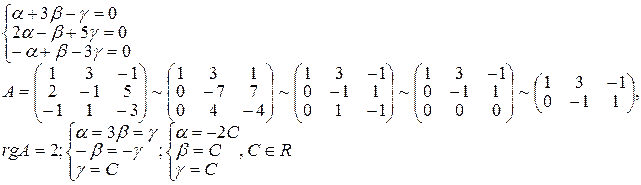
Коэффициенты равной нулю линейной комбинации векторов т,п,р могут быть отличны от нуля, следовательно векторыт,п,р линейно зависимы (компланарны). Подставляя α, β, γ в равенствo αт+βп+γp=0 и сокращая на С, получим -2т+ n+k = 0 .
С понятием линейной независимости векторов тесно связано такое фундаментальное понятие как базис.
Базисом на плоскости Q называется любая упорядоченная пара неколлинеарных векторов, параллельныx плоскости Q. Любой вектор с,
параллельный плоскости Q, можно представить в виде с= αа+ βb.
Базисом в трехмерном пространстве называется любая упорядоченная тройка некомпланарных (линейно-независимых) векторов. Если а,b,с- базис в пространстве, то любой вектор d пространства можно единственным образом разложить по этому базису по формуле:
d= αа+ βb+γc.
Декартовым базисом на плоскости (рмс 1.2.4) называются два единичных, взаимно-перпендикулярных вектора i и j (| i| = |j| =1, i^j ), совпадающих с положительным направлением осей ОХ и ОУ соответственно.

рис.1.2.4 рис.1.2.5
Любой вектор плоскости а может быть единственным образом представлен в виде a=ax i+ay j , где числа аx и аy называются координатами вектора а .
Декартовым базисом в пространстве (рис.1.2.5.) называются три
единичных взаимноперпендикулярных вектора i,j,k, совпадающих с положительным направлением осей OX,OY и OZ соответственно. Любой
вектор а может быть единственным образом представлен в виде
a=ax i+ay+az k , где числа аx , аy , аz называются координатами вектора а. Если вектор a=АВ задается координатами начальной точки A(xa , ya, za ) и конечной B(xb, yb, zb ), то его координаты имеют вид:
a=(xb-xa, yb-ya, zb-za ).
Два вектора а и b равны в том и только в том случае, когда координаты их равны, т.е. ax=bx, ay=by, az=bz.
