Оптимизация расходов рекламной кампании

Общие положения

Для понимания сути оптимизационных задач рассмотрим практический пример. Предположим, что магазин торгует магнитолами по цене 1500 руб. и телевизорами по цене 3000 руб. Требуется определить, сколько нужно продавать в день магнитол и телевизоров, чтобы выручка была максимальной.

Очевидный ответ будет таким: как можно больше телевизоров и как можно больше магнитофонов. При этом математическое уравнение будет иметь следующий вид:

S=1500*m+3000*n,

где S – выручка магазина,

m – количество проданных магнитол;

n – количество проданных телевизоров.

Реальные возможности магазина ограничены. Например, в день можно продать не более 70 магнитол и не более 50 телевизоров. Очевидно, что m и n не могут быть отрицательными значениями. Поэтому задав ограничения:

m<=50

n<=70

n>=0

m>=0

мы получим математическую модель, которую можно использовать для моделирования экономической ситуации.

Рассмотренный пример относится к области линейного программи­рования. Большое количество экономических задач сводятся к линейному программированию. Задачи линейного программирования можно решать, используя MS EXCEL.

Планирование производства

Завод выпускает два вида стали: легированную сталь и нелегированную сталь. Для производства стали используется руда от двух поставщиков: уральская руда и сибирская руда. Максимально возможные суточные запасы этих продуктов на складе завода составляют 20 т и 40 т соответственно. Расходы руды на производство 1 т. стали приведены в таблице 1.

Таблица 1. Расходы руды на производство стали

Исходный продукт	Расход на 1 т. стали	Максимальный запас руды
Легированная сталь	Нелегиро­ван­ная сталь
Уральская руда Сибирская руда

Анализ рынка показал, что суточный спрос на нелегированную сталь меньше спроса на легированную сталь не более чем на 2 т. Кроме того, установлено, что спрос на легированную сталь не превышает 10 т. в сутки. Прибыль от продажи одной тонны стали равны 4 000 р. и 3 000 р. соответственно. Необходимо найти общее количество выпускаемой стали, при котором при­быль максимальна.

Для решения задачи построим сначала математическую модель. Суммарная суточная прибыль от продажи стали составляет:

P=4000*L1+3000*L2,

где L1 – количество легированной стали

L2 – количество нелегированной стали

Перейдем к ограничениям. Объем производства не может быть отрицательным, следовательно

L1, L2 =>0

Расход исходного сырья не может превосходить максимального запаса, следовательно

2* L1 + 3* L2 <=20,

3* L1 + 4* L2 <=40.

Ограничение на спрос таковы, что должны выполняться неравенства

L1 – L2 <=2,

L1 <=10.

Теперь решим задачу, для чего выполните следующие действия.

1. Создайте таблицу по образцу, приведенному ни ниже (Рис. 45).

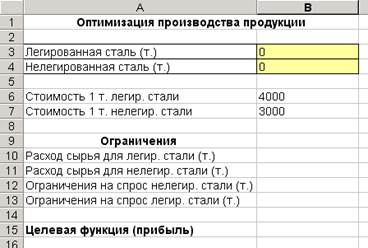
Рис. 45. Исходная таблица

2. Введите теперь формулы математической модели (Рис. 46).

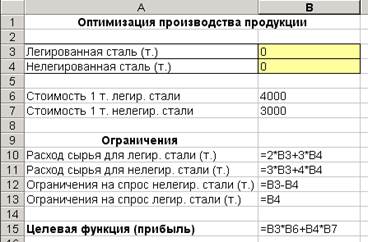
Рис. 46. Формулы математической модели

3. Выполните команду Сервис – Поиск решения.

4. В открывшемся окне задайте следующие параметры:

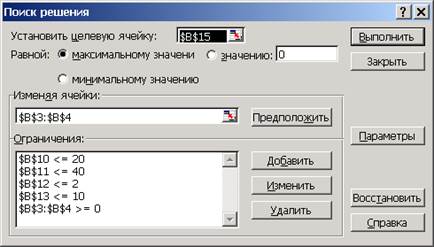
Рис. 47. Параметры поиска решения

5. После команды Выполнить откроется окно диалога Результаты поиска решения, которое сообщает, что решение найдено.

6. Создайте отчет о решении. Для этого выберите тип отчета - Результаты. Нажмите ОК.

7. В результате будут рассчитаны оптимальные значения производства стали (Рис. 48).

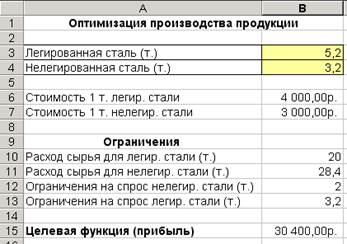
Рис. 48. Результаты решения

8. Для просмотра полученного отчета в рабочей книге (Рис. 49) выберите появившийся корешок.

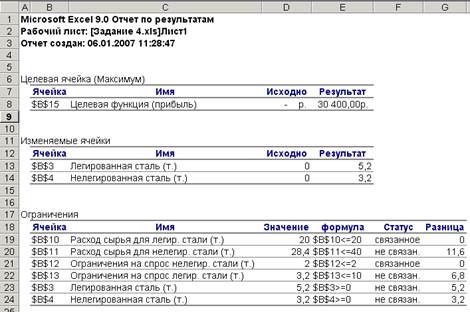
Рис. 49. Отчет по результатам решения

Оптимизация расходов рекламной кампании

Предприятие рекламирует свою деятельность с использованием четырех источников информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что вложенные в рекламу средства приводят к увеличению прибыли на 10, 5, 7 и 4 руб. соответственно в расчете на 1 руб., затраченный на рекламу. На рекламу выделено 50 000 руб., причем руководство намерено тратить на телевидение не более 50% выделенной суммы, на радио - не более 20%, на газеты - не более 35%, на расклейку объявлений - не более 30%. Как следует предприятию организовать рекламную кампанию, чтобы получить максимальную прибыль?

Построим экономико-математическую модель. Для этого введем следующие обозначения:

X₁ – средства, направленные на телевидение;

X₂ – средства, направленные на радио;

X₃ – средства, направленные на газеты;

X₄ – средства, направленные на расклейку объявлений.

Целевая функция будет иметь следующий вид:

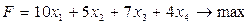
Ограничения:

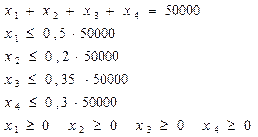
Теперь решим задачу в MS EXCEL. Для этого выполните следующие действия:

1. Создайте таблицу, приведенную на образце (Рис. 50).

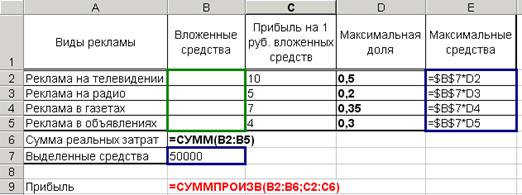
Рис. 50. Таблица для оптимизации рекламной деятельности

2. Вызовите функцию Поиск решения. Заполните поля поиска решения, учитывая, что ячейка В9 - целевая ячейка. В процессе решения задачи EXCEL будет перебирать значения в ячейках В2:В5 и вычислять значение общих затрат на рекламу по отдельным видам расходов. Т.е. у вас должны быть заполнены параметры Поиска решения следующим образом:

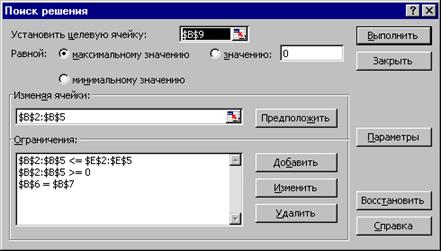
Рис. 51. Параметры поиска решения

3. После вычислений получим результат (Рис. 52).

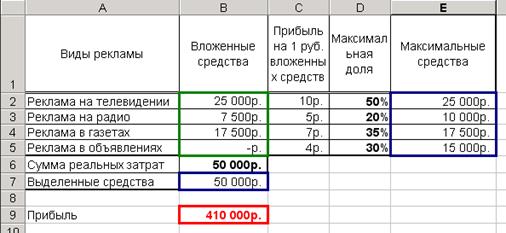
Рис. 52. Решение оптимизации рекламной деятельности

Из решения видно, что для максимизации прибыли выделять средства на расклейку объявлений не имеет смысла.

Транспортная задача

Имеется 4 склада продукции и 5 заводов по переработке этой продукции. Запасы продукции на складах составляют 150, 180, 145 и 200 тонн соответственно. Возможности заводов по переработке продукции составляют 100, 125, 140, 160 и 150 тонн соответственно.

Затраты на перевозку одной тонны продукции представлены в таблице 2.

Таблица 2. Затраты на перевозку одной тонны продукции

	Завод 1	Завод 2	Завод 3	Завод 4	Завод 5
Склад 1	14,32	18,24	16,22	24,12	19,56
Склад 2	18,33	16,42	13,75	21,48	11,85
Склад 3	13,45	14,26	17,15	18,95	15,45
Склад 4	15,55	15,95	15,12	19,42	16,44

Общее количество перевозимой продукции сбалансировано. Т.е. вся продукция полностью перерабатывается заводами. Требуется ответить на вопрос – как организовать перевозку продукции, чтобы затраты были минимальны?

Построим экономико-математическую модель. Для этого введем следующие обозначения:

Х_ij – количество продукции, перевозимой с i-го склада на
j-ый завод.

C_ij – стоимость перевозки единицы продукции с i-го склада на j-ый завод,

Y – затраты на перевозку всей продукции.

Затраты на перевозку всей продукции можно определить по формуле:

Y = SS X_ij×С_ij

Это и будет наша целевая функция. Ее значение должно быть минимальным. Введем теперь ограничения. Обозначим:

N_i – запасы продукции на i-ом складе,

M_j – возможности j-го завода по переработке продукции.

Тогда ограничения можно записать в следующем виде:

N_i = S X_i;

M_j = S X_j;

X_ij ≥ 0;

X_ij – целые.

Для X_ij задается ограничение на целые значения, чтобы программа тратила меньше времени на перебор всех возможных значений. Хотя это ограничение не является обязательным.

Теперь решим задачу в MS EXCEL. Решение будет состоять из следующих этапов:

1-й этап. На этом этапе создадим таблицу с исходными данными.

2-й этап.. На этом этапе создадим таблицу, в которой EXCEL будет находить оптимальные значения объемов продукции, которую надо перевести со складов на заводы.

3-й этап. Создадим таблицу, в которой EXCEL будет вести расчет стоимости перевозимой продукции со складов на заводы. С помощью этой таблицы мы получим общие затраты на перевозку.

4-й этап. Решим задачу, используя функцию Поиск решения.

1. Создайте таблицу в EXCEL по образцу (Рис. 53).

	A	B	C	D	E	F	G	H
		Завод 1	Завод 2	Завод 3	Завод 4	Завод 5		Имеется
	Склад 1	14,32	18,24	16,22	24,12	19,56
	Склад 2	18,33	16,42	13,75	21,48	11,85
	Склад 3	13,45	14,26	17,15	18,95	15,45
	Склад 4	15,55	15,95	15,12	19,42	16,44
	Требуется

Рис. 53. Исходная таблица

В ячейках B2:F5 расположены значения стоимости перевозок 1 тонны продукции. В ячейках Н2:Н5 находятся значения запасов продукции на складах в тоннах. В ячейках В7:F7 находятся значения возможностей заводов по переработки продукции.

В ячейке H7 находится формула =СУММ(H2:H5).

2. Создайте ниже следующую таблицу (Рис. 54).

	A	B	C	D	E	F	G	H
	Оптимальный план перевозок
		Завод 1	Завод 2	Завод 3	Завод 4	Завод 5
	Склад 1
	Склад 2
	Склад 3
	Склад 4

Рис. 54. Таблица для расчетов

В этой таблице в ячейках B11:F14 EXCEL будет искать значения, удовлетворяющие условиям задачи.

3. В ячейку Н11 введите формулу: = СУММ(В11:F11)

4. Скопируйте эту формулу в ячейки Н12:Н14.

5. В ячейку В16 введите формулу: = СУММ(В11:В14)

6. Скопируйте эту формулу в ячейки С16:F16.

7. В ячейку Н16 ввести формулу: = СУММ(Н11:Н14)

Таким образом, в ячейках Н11:Н14 будут находиться значения объемов продукции, вывезенной со складов, а в ячейках В16:F16 будут находиться значения объемов продукции, доставленной на заводы. В ячейке Н16 будет определено общее количество перевезенной продукции.

Перед решением задачи в этих ячейках EXCEL поместит нули (Рис. 55).

	A	B	C	D	E	F	G	H
	Оптимальный план перевозок
		Завод 1	Завод 2	Завод 3	Завод 4	Завод 5
	Склад 1
	Склад 2
	Склад 3
	Склад 4

Рис. 55. Таблица объемов перевозок

8. Теперь определим затраты на перевозку продукции с каждого склада на каждый завод. Составим следующую таблицу (ее можно скопировать с предыдущей таблицы):

	A	B	C	D	E	F	G	H
	Затраты на перевозку
		Завод 1	Завод 2	Завод 3	Завод 4	Завод 5
	Склад 1
	Склад 2
	Склад 3
	Склад 4

Рис. 56. Таблица затрат на перевозку продукции

9. В ячейку В20 введите формулу: =В2*В11.

10. Скопируйте эту формулу в блок ячеек В20:F23. В таблице в указанных ячейках появятся нули.

11. В ячейку Н20 введите формулу: =СУММ(В20:F20).

12. Скопируйте эту формулу в ячейки Н21:Н23.

13. В ячейку В25 введите формулу: =СУММ(В20:В23).

14. Скопируйте эту формулу в ячейки С25:F25.

15. В ячейку Н25 введите формулу: =СУММ(Н20:Н23).

Таким образом, в ячейках Н20:Н23 будут находиться значения затратна перевозку продукции, вывезенной со складов, а в ячейках В25:F25 будут находиться значения затрат на перевозку продукции, доставленной на заводы. В ячейке Н25 будут определены общие затраты на перевозку продукции. Перед решением задачи в этих ячейках EXCEL также поместит нули. Тогда общий вид рабочего листа будет следующим (Рис. 57):

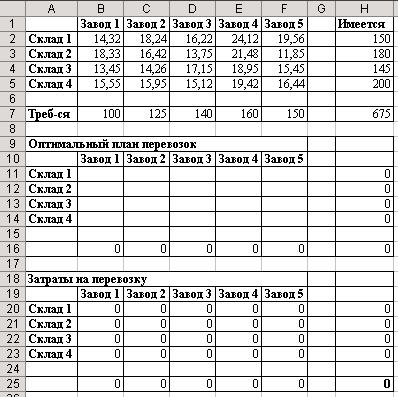
Рис. 57. Вид рабочего листа перед решением

Ячейка Н25 будет целевой ячейкой. EXCEL в процессе решения задачи будет перебирать значения в ячейках В11:F14 и вычислять значение общих затрат на перевозку. Затем он выберет тот вариант, при котором значение в целевой ячейке будет минимальным.

16. Установите курсор на ячейку Н25 и выполните команду Сервис - Поиск решения.

17. Задайте параметры Поиска решения (Рис. 58).

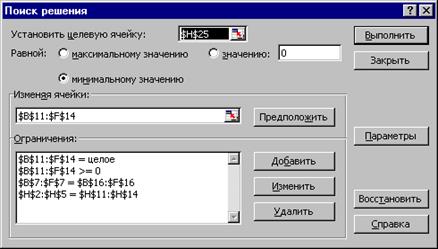
Рис. 58. Параметры поиска решения

После выполнения поиска решения получим следующий результат (Рис. 59):

Из полученного решения видно, что на первый завод с первого склада нужно перевезти 100 тонн продукции. На второй завод необходимо перевезти 125 тонн с третьего склада и т.д.

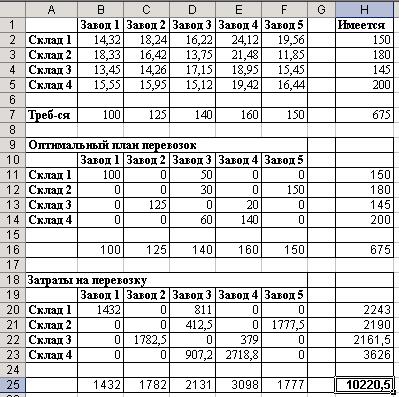
Рис. 59. Результат поиска решения