Нарушение закона Дарси. Нелинейные законы фильтрации

При малых и больших скоростях фильтрации закон Дарси не выполняется. Нарушение закона Дарси при малых скоростях обычно связано с неньютоновскими свойствами нефти.

При больших скоростях начинают проявляться инерционные силы, которые возникают при движении жидкости по извилистому пористому каналу. Проведем аналогию с трубной гидравликой. Потери давления пропорциональны скорости, как при ламинарном режиме движения жидкости в трубе, так и при фильтрации жидкости по закону Дарси. Потери давления пропорциональны квадрату скорости, как при сильно развитом турбулентном режиме движения жидкости в трубе, так и при больших скоростях фильтрации (закон Дарси не выполняется).

В трубной гидравлике режим движения определяется по числу Рейнольдса:

,

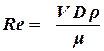(1.26)

где V – средняя скорость в трубе;

D – диаметр трубы.

Если число Рейнольдса меньше критического Re_кр = 2320, то режим движения ламинарный, а если больше, то турбулентный. При ламинарном движении потери давления пропорциональны скорости ∆p ~ u, а при турбулентном режиме потери давления пропорциональны квадрату скорости ∆p ~ u².

По аналогии введем число Рейнольдса и при фильтрации. Различными авторами предложено несколько формул для определения числа Рейнольдса, но приведем одну из них – формулу Щелкачева, в которой за характерную скорость принята скорость фильтрации u, за характерный поперечный размер капилляра – корень квадратный из проницаемости пласта. Кроме этого добавлен множитель, который частично учитывает структуру пористой среды – 10/m^2,3.

Формула Щелкачева имеет вид:

.

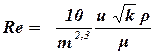(1.27)

Так как при одной и той же пористости и проницаемости структура пористой среды может быть разной, то широк разброс в значении критического значения числа Рейнольдса Re_кр = 0,032 – 14. Обычно принимают Re_кр = 1. Если вычисленное значение числа Re оказывается меньше нижнего критического значения, то закон Дарси справедлив, если больше верхнего значения, то закон Дарси заведомо нарушен. Скорость фильтрации, при которой нарушается закон Дарси, называется критической скоростью фильтрации (u_кр).

Однако нарушение линейного закона фильтрации еще не означает перехода от ламинарного движения к турбулентному. Закон Дарси нарушается вследствие того, что силы инерции, возникающие в жидкости за счет извилистости каналов и изменения площади их поперечных сечений, становятся при u > u_кр соизмеримыми с силами трения.

Для практических расчетов число Рейнольдса удобнее выражать через массовый расход. Это связано с тем обстоятельством, что при фильтрации газа плотность газа зависит от давления в поперечном сечении, поэтому необходимо эту плотность рассчитывать дополнительно:

.

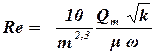(1.28)

При нарушении закона Дарси зависимость между скоростью фильтрации и градиентом давления dp/ds лучше всего описывается двучленной формулой. Ее еще называют формулой Форхгеймера:

,

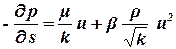(1.29)

где k – коэффициент проницаемости пористой среды, м²;

m – коэффициент динамической вязкости жидкости, Па×с;

r – плотность жидкости, кг/м³;

g – ускорение свободного падения, м/с².

b – безразмерный коэффициент, характеризующий структуру пористой среды.

При малых значениях скорости вторым слагаемым можно пренебречь, и тогда получим закон Дарси. При больших значениях скоростей первым слагаемым можно пренебречь, тогда получим закон Краснопольского:

.

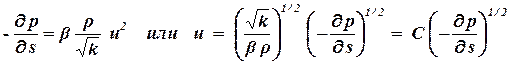(1.30)

Иногда при нарушении закона Дарси используют одночленный закон фильтрации в виде:

,

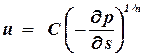(1.31)

где С и n некоторые постоянные числа 1 < n < 2.

В нефтяных скважинах нарушение закона Дарси происходит достаточно редко; большинство газовых скважин работают при нарушении этого закона.

При малых скоростях также происходит нарушение закона Дарси. Это связано или с большой площадью соприкосновения породы и жидкости (внизкопроницаемых коллекторах) или с наличием в нефти смол, парафинов и других причин. В этом случае закон Дарси можно записать в виде:

,

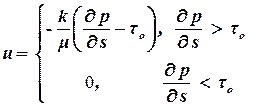(1.32)

где t_o – начальный градиент давления.