Завдання на лабораторну роботу. Інтерполяційні поліноми Лагранжа
Лабораторна робота № 5.
Інтерполяційні поліноми Лагранжа. Сплайн-інтерполяція.
Мета роботи:познайомитися з методами інтерполяції складних функцій, реалізувати заданий за варіантом метод інтерполяції у середовищі МatLAB.
Завдання до виконання роботи:Доповнити систему МatLAB файлом, що реалізує заданий метод інтерполяції (відповідно до варіанту).
Теоретичні відомості.
Інтерполяційний поліном Лагранжа.Французький математик Жозеф Луї Лагранж (1736-1813 р.р.) запропонував для побудови інтерполяційних поліномів наступний метод. Для двох вузлових точок (х0, у0), (х1, у1) він записав:
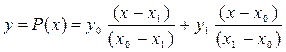(5.2)
Відношення при уі називаються коефіцієнтами Лагранжа. Побудуємо коефіцієнти Лагранжа для n точок. Особливість їх побудови полягає у виключенні з ряду різниць, що перемножуються у чисельнику і знаменнику, різниці зі значенням хі після знаку “–”. Для n точок коефіцієнт Лагранжа запишемо у загальному вигляді так:
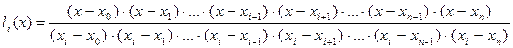(5.3)
Інтерполяційний поліном Лагранжа має вигляд:
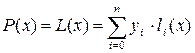(5.4)
Він дозволяє досить просто побудувати наближення функції по відомим вузловим точкам.
При сплайн-інтерполяції зберігається умова проходження наближуючої функції через вузлові точки. Сплайн (spline) переводиться з англійської, як глучка лінійка. Сплайн-функції різняться ступенем поліному, що зображає функцію. Сутністю сплайн-інтерполяції є моделювання фрагментів заданої функції рядом поліномів низького ступеню. Прикладом такого інтерполювання є кусково-лінійне інтерполювання (рис. 5.1), де кожна з функцій будується по двом сусіднім вузловим точкам. Такий же принцип побудови зберігається і для формування поліномів вищих порядків, тільки кількість точок, на основі яких будується кожен з поліномів може бути більшою. Так, наприклад, для кусково-квадратичного поліному на проміжку [x0, xN] береться кожен інтервал [x2k, x2k+2] для побудови на ньому квадратичного поліному. Але при побудові такого сплайну кривизна в парних вузлах різко змінюється, що відбивається на якості аппроксимації.
Найбільш оптимальною на даний момент є кусково-кубічна сплайн-інтерполяція. Вона широко застосовується у системах комп‘ютерної графіки та системах проектування з використанням комп‘ютера (CAD-системах).
За допомогою цього виду інтерполяції можливо побудувати гладку криву, що проходить через задані точки.
Загальний вираз для кубічної сплайн-функції Sk(x) має вигляд:
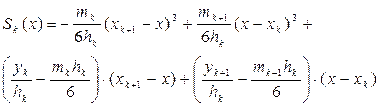, (5.5)
кубічний поліноми для утворення сплайн-функції будується по трьом сусіднім точкам за загальною формулою:
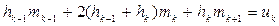(5.6)
де hk = xk+1 - xk , mk = S’’(xk), uk = 6(dk – dk-1), де в свою чергу dk = (yk+1 – yk)/hk .
При отриманні сплайн функції будуються N-1 рівнянь з N+1змінними. Для їх розв‘язання систему треба доповнити двома додатковими рівняннями. В якості таких рівнянь вибирають обмеження в крайніх точках сплайну (див. табл. 5.1).
Таблиця 5.1
Обмеження в крайніх точках кубічного сплайну.
| № | Тип сплайну | Обмеження в крайніх точках |
| Зімкнений кубічний сплайн (найкращий, якщо відомі похідні): задається S’(x0), S’(xn) |   | |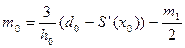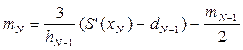
| Природній кубічний сплайн (“релаксована крива”) | m0 = 0, mN = 0 | |
| Екстраполювання S’’(х) в крайніх обмежуючих точках |   | |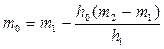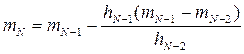
| S’’(х) постійна біля крайніх точок | m0 = m1 , mN = mN-1 | |
| Задання S’’(х) в кожній крайній точці | m0 = S’’(x0) , mN = S’’(xN) |
Розглянемо побудову зімкненого кубічного сплайну. Якщо відома перша похідна у початковій точці, можна обчислити m0 і перше рівняння прийме вигляд:
2(h0 + h1)m1 + h1m2 = u1 – h0m0 (5.7)
Аналогічно обчислюємо останнє рівняння:
hN-2mN-2 + 2(hN-2 + hN-1)mN-1 = uN-1 – hN-1mN . (5.8)
Отримуємо тридіагональну лінійну систему рівнянь:
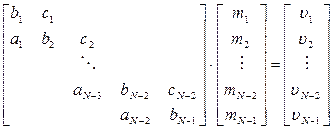(5.9)
Коефіцієнти сплайну обчислюємо за формулами:
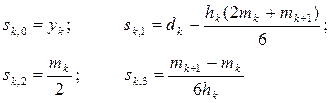(5.10)
Для зручності обчислень кожен кубічний сплайн доцільно записувати у формі вкладених перемножень:
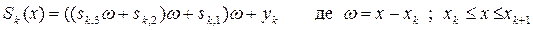(5.11)
Завдання на лабораторну роботу.
Побудувати поліном Лагранжа для функції заданої таблично (відповідно до варіанту). Побудувати по цим же точкам кубічний сплайн. Побудувати функції для обох поліномів і на окремому графіку – функцію, що зображає різницю занчень у невузлових точках (прораховувати значення не менш, як у 3-х невузлових точках між кожними двома вузлами).
| Варіант | Координати вузлових точок | Тип кубічного сплайну | ||||
| (1, 3) | (3, 7) | (6, 9) | (10, 8) | (14, 11) | Зімкнений | |
Лістинг програми
Функція обчислення поліному Лагранжа:
function f = Lagrange(X,Y,t)
f = 0;
n = 5;
for i = 1:n
l=1;
for j = 1:n
if not (j==i)
l = l*(t-X(j))/(X(i)-X(j));
end
end
f = f+l*Y(i);
end
Функція побудови графіка за допомогою полінома Лагранжа та сплайн інтерполяції:
function PlotAll(X,Y,k)
step = (X(5)-X(1))/k;
H(1) = X(1);
S(1) = Spline(X,Y,H(1));
L(1) = Lagrange(X,Y,H(1));
for i = 2:k+1
H(i) = H(i-1)+step;
S(i) = Spline(X,Y,H(i));
L(i) = Lagrange(X,Y,H(i));
end
plot(H,S,'r',H,L,'b',X,Y,'black')
Функція обчислення кубічної сплайн-функції:
function s=Spline(X,Y,x)
dx0 = (Y(2)-Y(1))/(X(2)-X(1));
dxn = (Y(5)-Y(4))/(X(5)-X(4));
for i = 1:4
H(i) = X(i+1)-X(i)
D(i) = (Y(i+1)-Y(i))/H(i)
if i~=1
U(i) = 6*(D(i)-D(i-1))
end
end
U(1) = (3/H(1))*(D(1)-dx0)
U(5) = (3/H(4))*(dxn-D(4))
A = zeros(5)
A(1,1) = H(1)+H(2)
A(1,2) = (H(1)+H(2))/2
for i = 2:4
A(i,i-1) = H(i-1)
A(i,i) = 2*(H(i-1)+H(i))
A(i,i+1) = H(i)
end
A(5,4) = (H(1)+H(2))/2
A(5,5) = H(1)+H(2)
M = U/A
for k = 1:4
if (x<=X(k+1))
break
end
end
w = x-X(k)
s0 = Y(k)
s1 = D(k)-H(k)*(2*M(k)+M(k+1))/6
s2 = M(k)/2
s3 = (M(k+1)-M(k))/(6*H(k))
s = ((s3*w+s2)*w+s1)*w+s0
Результати роботи програм
На рис.1 наведені графіки функцій, отриманих в результаті застосування сплайн інтерполяції та поліному Лагранжа щодо вихідних даних. Червоним кольором позначена функція сплайн інтерполяції, червоним – Лагранжа. На рис.2 наведено графік різниці функцій Лагранжа та сплайн інтеополяції.
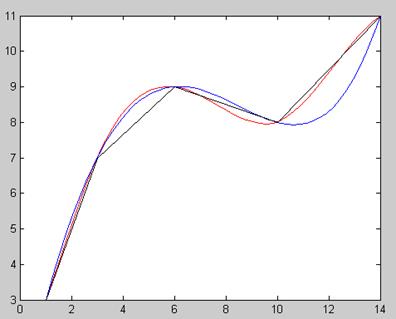
Рис.1. Отримані графіки
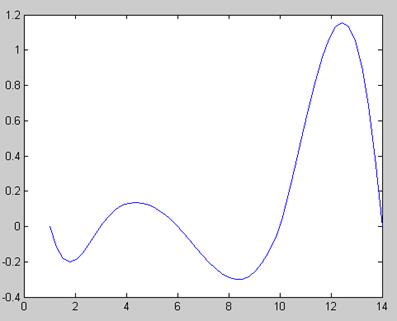
Рис.2. Різниця значень
Висновок: на цій лабораторній роботі було розглянуто методи інтерполяції складних функцій, було побудовано функції за заданими вузловими точками.