Визначення символа Лежандра
№1
Комплексні числа
Розглянемо рівняння 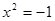 , це ріняння має розв’язок в множині комплексних чисел, його позначимо через
, це ріняння має розв’язок в множині комплексних чисел, його позначимо через 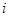 . Тоді
. Тоді 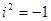 . Множина
. Множина 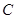 - розширення множини дійсних чисел
- розширення множини дійсних чисел 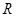 , тому
, тому 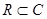 . Для елементів множини
. Для елементів множини 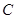 введемо арифметичні операції:
введемо арифметичні операції: 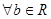
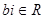
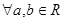
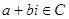 . Ці числа
. Ці числа 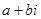 складові множини
складові множини 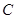 .
.
Комплексним числом називається число вигляду 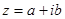 , де
, де 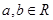 . Якщо
. Якщо 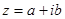 то
то 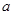 - дійсна частина
- дійсна частина 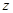 , а
, а 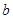 - уявна частина комплексного числа
- уявна частина комплексного числа 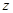 . Якщо
. Якщо 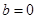 одержимо, що
одержимо, що 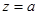 , дійсне число, якщо
, дійсне число, якщо 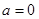 , то
, то 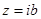 - чисто уявне комплексне число.
- чисто уявне комплексне число.
Числа 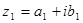 і
і 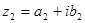 вважєють рівними якщо рівні їх дійсні та уявні частини, тобто
вважєють рівними якщо рівні їх дійсні та уявні частини, тобто 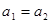 ,
, 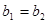 .
.
Нехай 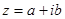 комплексне число, тоді комплексноспряженим до нього назвемо число
комплексне число, тоді комплексноспряженим до нього назвемо число 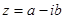 .
.
Дії над комплексними числами
1. Під сумою двох чисел 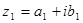 та
та 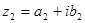 будемо розуміти наступне
будемо розуміти наступне
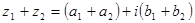
2. Під різницею двох чисел 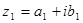 та
та 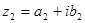 будемо розуміти наступне
будемо розуміти наступне
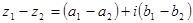
3. Під добутком двох чисел 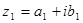 та
та 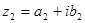 будемо розуміти наступне
будемо розуміти наступне
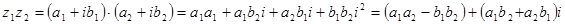
4. Під діленням двох чисел 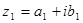 та
та 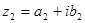 ,
, 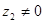 будемо розуміти наступне
будемо розуміти наступне
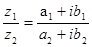 , домножимо чисельник і знаменник на комплексно спряжене з знаменником
, домножимо чисельник і знаменник на комплексно спряжене з знаменником
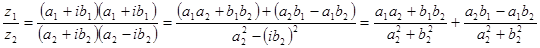
Тригонометрична форма комплексного числа
Кожному комплексному числу відповідає деякий вектор на площині, а будь-який вектор задається довжиною і напрямком. Наприклад вектор 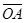 можна задати кут якій цей вектор утворює з додатним напрямком осі
можна задати кут якій цей вектор утворює з додатним напрямком осі 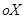 . Домомвимось, що всі кути відраховуються від осі
. Домомвимось, що всі кути відраховуються від осі 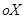 проти годинникової стрілки.
проти годинникової стрілки.
Нехай 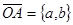 `відповідає комплексному числу
`відповідає комплексному числу 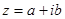 позначимо через
позначимо через 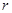 довжину вектора
довжину вектора 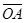 , а через
, а через 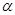 кут, який утворює цей вектор з додатним напрямком осі
кут, який утворює цей вектор з додатним напрямком осі 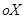 , тоді
, тоді
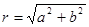
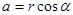
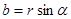
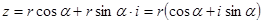
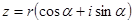 - тригонометрична форма комплексного числа.
- тригонометрична форма комплексного числа.
Назвемо 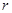 - модулем комплексного числа , а
- модулем комплексного числа , а 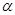 - аргумент комплексного числа (
- аргумент комплексного числа ( 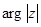 , якщо
, якщо 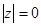 , то аргумент не визначається).
, то аргумент не визначається).
Нехай 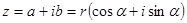 , тоді
, тоді 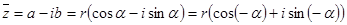
Для даного комплексного числа 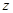 його модуль визначається точно, а аргумент з точністю до періода. Таким чином два числа в тригонометричні формі вважаються рівними, якщо їх модулі рівні, а аргументи відрізняються на число кратне
його модуль визначається точно, а аргумент з точністю до періода. Таким чином два числа в тригонометричні формі вважаються рівними, якщо їх модулі рівні, а аргументи відрізняються на число кратне 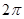
Множення комплексних чисел в тригонометричній формі
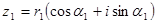
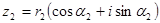
Щоб перемножити комплексні числа в тригонометричному вигляді треба модулі цих чисел помножити а аргументи додати.
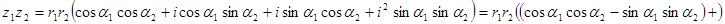
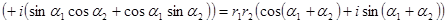
Розглянемо випадок множення двох спряжених комплексних чисел в тригонометричній формі
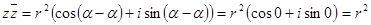 .
.
Ділення комплексних чисел втригонометричній формі
Дані два числа втригонометричній формі
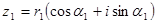
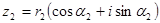
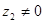
Домножимо чисельник і знаменник на число комплексно спряжене до знаменника:
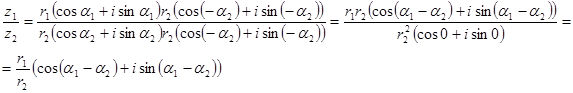
Тобто, щоб поділити два комплексних числа втиригонометричній формі потрібно поділити модулі, а аргументи відняти.
№2
Формула Муавра
Нехай 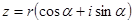 комплексне число. Необхідно піднести задане число в
комплексне число. Необхідно піднести задане число в 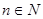 степінь. Скористаємося правилом множення комплексних чисел:
степінь. Скористаємося правилом множення комплексних чисел:
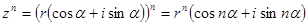
Розглянемо випадок коли 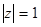 , тоді
, тоді 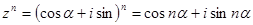 .
.
Доведемо, що формула Муавра вірна для будь-яких цілих степенів. Припустимо 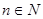 і число
і число 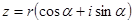 необхідно піднести в степінь
необхідно піднести в степінь 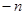 при
при 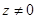 . Маємо:
. Маємо:
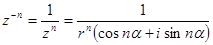 Запишемо 1 у тригонометричному вигляді:
Запишемо 1 у тригонометричному вигляді: 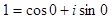 і перепишемо представлення формули для
і перепишемо представлення формули для 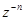 . Маємо:
. Маємо:
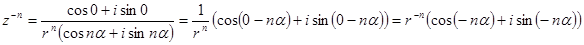 .
.
Приклад застосування формули Муавра
Виразити 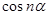 і
і 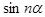 через
через 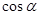 ,
, 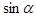 .
.
Розглянемо комплексне число 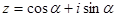 . За формулою Муавра маємо
. За формулою Муавра маємо 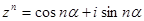 , а з іншого боку за формулою Бінома:
, а з іншого боку за формулою Бінома:
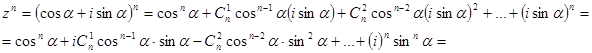
прирівняємо дійсні та уявні частини:
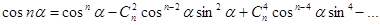
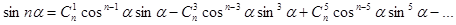
Корені комплексного числа
Припустимо зафіксоване комплексне число 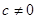 знайдемо всі корені степеня
знайдемо всі корені степеня 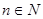 числа
числа 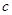 , якщо вони існують. Запишемо
, якщо вони існують. Запишемо 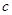 в тригонометричній формі:
в тригонометричній формі: 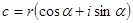 . Припустимо
. Припустимо 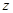 є коренем
є коренем 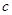 в
в 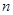 степені, тобто
степені, тобто 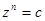 . Запишемо
. Запишемо 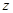 в тригонометричній формі:
в тригонометричній формі: 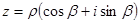 , тоді за фомулою Муавра маємо:
, тоді за фомулою Муавра маємо:
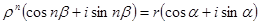
прирівняємо модулі 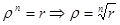 . Тобто модуль числа
. Тобто модуль числа 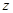 визначається однозначно. Крім цього виконується
визначається однозначно. Крім цього виконується 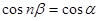
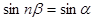
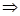
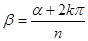 .
.
Розглянемо варіанти:
1. 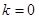 , тоді
, тоді 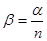 і
і 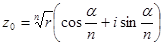 ;
;
2. 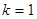 , тоді
, тоді 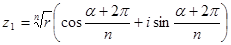 ;
;
3. 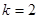 , тоді
, тоді 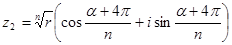 ;
;
4. 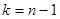 , тоді
, тоді 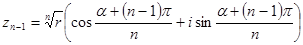 ;
;
5. 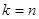 , тоді
, тоді 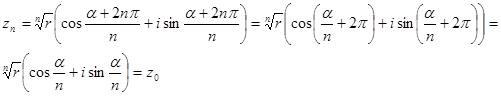
6. 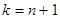 , тоді
, тоді 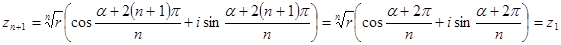
Покажемо, що 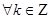 справедлива наступна нерівність:
справедлива наступна нерівність:
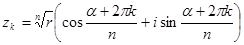 і співпадає з одним із чисел
і співпадає з одним із чисел 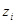
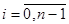
Поділимо 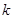 на
на 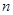 з залишком
з залишком 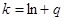 , де
, де 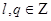 і
і 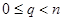 , тоді
, тоді 
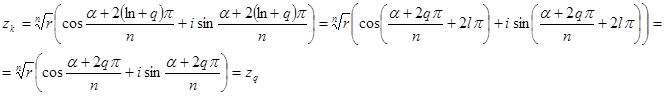
де 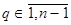 . Покажемо всі
. Покажемо всі 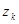 є коренями степя
є коренями степя 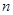 . За формулою Муавра маємо:
. За формулою Муавра маємо:
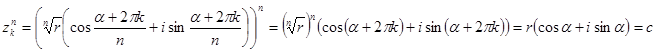
Оскільки при переході від 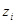 до
до 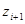 аргумент зростає на
аргумент зростає на 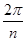 то всі корені
то всі корені 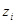
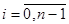 різні. Таким чином для кожного комплексного числа
різні. Таким чином для кожного комплексного числа 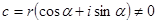 існує в точності
існує в точності 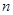 коренів
коренів 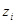
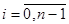 , які визначаються за таким правилом
, які визначаються за таким правилом 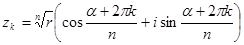 при
при 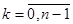 . Точки, що відповідають
. Точки, що відповідають 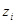 знаходяться на колі радіуса
знаходяться на колі радіуса 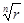 , і ділять це коло на
, і ділять це коло на 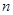 рівних частин.
рівних частин.
№3
№4
Алгоритм Евкліда
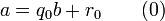
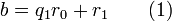
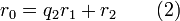
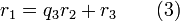
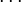
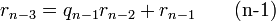
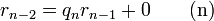
Алгоритм Евкліда ітеративний, тобто, пошук розв'язку відбувається за декілька кроків. Для того щоб знайти НСД(a, b) на 0-му кроці знаходять остачу r0 від ділення a на b. На 1-му кроці знаходять остачу від ділення b на r0. Оскільки залишки зменшуються на кожному кроці але не можуть бути від'ємними, то цю операцію виконують n кроків до тих пір поки не отримують остачу 0. Найбільшим спільним дільником є остання не нульова остача rn−1. Кількість кроків в алгоритмі має бути скінченною, оскільки існує лише скінченна кількість цілих чисел між початковим залишком r0 та нулем.
[ред.]Доведення Алгоритму Евкліда
Правильність алгоритму Евкліда можна довести за два кроки.[14] Спочатку необхідно довести, що rn−1 дійсно є дільником a та b, а потім необхідно довести, що це є найбільший спільний дільник.
[ред.]Доведення, що rn − 1 є дільником a та b
З n-го кроку випливає, що 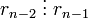 (rn − 2 ділиться на rn − 1). Підставимо
(rn − 2 ділиться на rn − 1). Підставимо 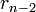 в n-1-ий крок. Маємо:
в n-1-ий крок. Маємо:
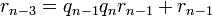
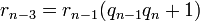
Таким чином 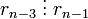 . Повторимо цю опрацію n разів і отримаємо, що
. Повторимо цю опрацію n разів і отримаємо, що 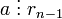 та
та 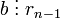 . Отже,
. Отже, 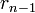 є дільником a та b.
є дільником a та b.
[ред.]Доведення, що rn − 1 є найбільшим дільником a та b
За означенням число 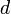 називається найбільшим спільним дільником a та b, тоді і тільки тоді, коли для будь-якого числа
називається найбільшим спільним дільником a та b, тоді і тільки тоді, коли для будь-якого числа 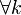 для якого виконується:
для якого виконується: 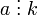 та
та 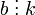 має виконуватись, що
має виконуватись, що 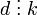 .
.
Нехай k є дільником a та b, тоді 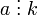 та
та 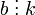 або можна сказати, що існують такі числа
або можна сказати, що існують такі числа 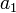 та
та 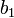 , що
, що
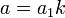
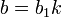
Підставимо в 1-ий крок алгоритму:
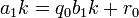 і виконаємо перетворення:
і виконаємо перетворення:
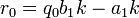
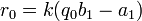
Отже, 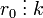 . Підставимо
. Підставимо 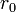 в 2-ий крок і аналогічно продовжимо до тих пір поки з останнього кроку не отримаємо, що
в 2-ий крок і аналогічно продовжимо до тих пір поки з останнього кроку не отримаємо, що 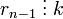 , що доводить те, що
, що доводить те, що 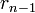 є найбільшим спільним дільником.
є найбільшим спільним дільником.
№5
Теорема про найбільший спільний дільник
Нехай 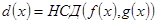 , тоді існують такі многочлени
, тоді існують такі многочлени 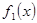 і
і 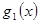 , що
, що 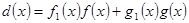 при цьому
при цьому 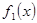 і
і 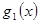 можна вибрати так, що ст
можна вибрати так, що ст 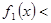 ст
ст 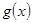 , ст
, ст 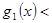 ст
ст  .
.
(Доведення)
Припустимо 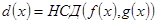
 і
і 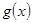 ненульові многочлени. Доведення існування
ненульові многочлени. Доведення існування 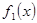 і
і 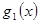 можна провести двома способами.
можна провести двома способами.
І спосіб. Позначимо через 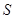 таку множину многочленів
таку множину многочленів 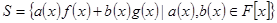 , зрозуміло, що
, зрозуміло, що 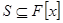 . Визначимо властивості множини
. Визначимо властивості множини 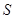 :
:
1. 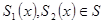 тоді
тоді 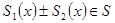 .
. 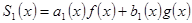 і
і 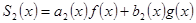 .
. 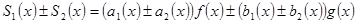
2. Якщо 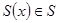 і
і 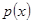 довільний многочлен, який не обов’язково належить
довільний многочлен, який не обов’язково належить 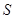 , то
, то 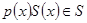
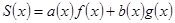 і
і 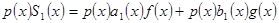 .
.
3. Якщо деякий многочлен 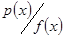 і
і 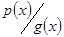 то
то 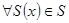
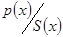
4. 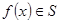 і
і 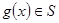 .
. 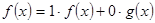 ,
, 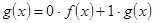 .
.
З множини 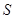 виберемо ненульовий многочлен найбільшого степеня і позначимо його
виберемо ненульовий многочлен найбільшого степеня і позначимо його 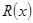 . З (3) якщо
. З (3) якщо 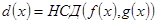 то
то 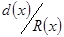 . Покажемо, що довільний многочлен із
. Покажемо, що довільний многочлен із 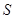 ділиться на
ділиться на 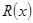 . Від супротивного нехай деякий многочлен
. Від супротивного нехай деякий многочлен 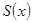 не ділиться на
не ділиться на 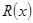 тоді поділимо його із залишком.
тоді поділимо його із залишком.
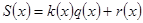 при цьому ст
при цьому ст 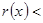 ст
ст 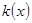
Враховуючи властивості (1),(2) 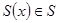 ,
, 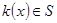 , тому
, тому 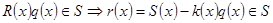 і вмножині
і вмножині 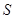 знайдеться ненульовий многочлен
знайдеться ненульовий многочлен 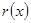 степінь якого меньше степеня
степінь якого меньше степеня 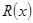 , що суперечить вибору
, що суперечить вибору 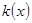 , тому
, тому 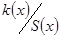 . За властивістю (4)
. За властивістю (4) 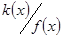 ,
, 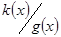 . З означення НСД одержимо
. З означення НСД одержимо 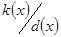 , раніше було одержано, що
, раніше було одержано, що 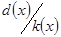 , тому многочлени
, тому многочлени 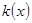 і
і 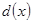 різняться лише на сталий множник і є асаційовними. З означення асоційовності
різняться лише на сталий множник і є асаційовними. З означення асоційовності 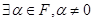 такий, що
такий, що 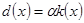 і за властивість (2)
і за властивість (2) 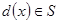 . За означення множини
. За означення множини 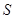 існують такі многочлени
існують такі многочлени 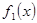 і
і 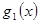 :
: 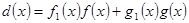 .
.
ІІ спосіб. Конструктивний, тому дає змогу знайти 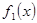 і
і 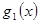 . Нехай
. Нехай 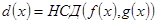 і для визначеності ст
і для визначеності ст 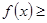 ст
ст 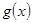 . Будемо знаходити НСД за допомогою алгоритма Евкліда.
. Будемо знаходити НСД за допомогою алгоритма Евкліда.
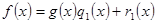 і
і 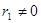
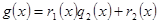 і
і 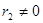
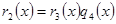 тобто
тобто 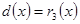 , тоді підставимо вирази:
, тоді підставимо вирази:
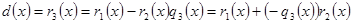
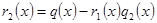
Підставляємо значення. Маємо:
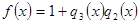 ,
, 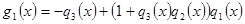
№6
Схема Горнера та її застосування
 ,
, 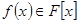 . Поділимо
. Поділимо  на
на 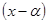 з остачею.
з остачею. 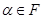
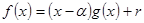 , де
, де 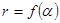 і ст
і ст 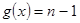 .
. 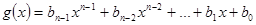 . Підставимо
. Підставимо 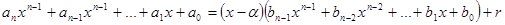 . Прирівняємо коефіцієнти при відповідних степенях маємо:
. Прирівняємо коефіцієнти при відповідних степенях маємо:
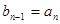
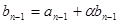
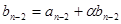
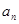 | 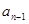 | 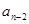 | 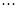 | 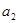 | 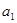 | 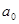 | |
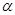 | 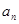 | 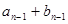 | 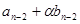 | 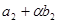 | 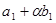 | 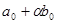 | |
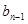 | 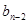 | 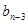 | 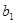 | 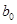 | 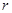 |
Приклад застосування.
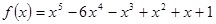 по степеням
по степеням 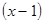 .
.
Поділимо  на
на 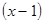 із залишком.
із залишком. 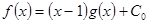 , де
, де 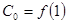 .
.
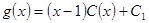 ,
, 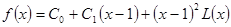 .
.
| -6 | -1 | |||||
| 1*1-6 | -5+1 | -5 | -4 | -4*1+1 | ||
| -4 | -10 | -15 | -19 | |||
| -3 | -13 | -28 | ||||
| 1*1-3 | -2*1-15 | 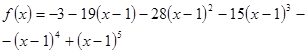 | ||||
| -1 | ||||||
№7
Незвідні многочлени та основна теорема про подільність многочлена
Як відомо простим числом називається число 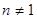 і дільниками числа
і дільниками числа 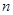 хє саме число і 1. Аналогічним чином в кільці многочленів є незвідні многочлени .
хє саме число і 1. Аналогічним чином в кільці многочленів є незвідні многочлени .
Многочлен 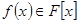 є незвідним над полем
є незвідним над полем 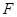 якщо з того що
якщо з того що 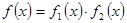 і
і 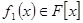 ,
, 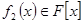 слідує, що степінь одного із многочленів рівна нулю, тобтохоч один із многочленів рівний
слідує, що степінь одного із многочленів рівна нулю, тобтохоч один із многочленів рівний 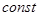 .
.
Лема (про незвідні многочлени).
Нехай 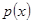 - незвідний многочлен і
- незвідний многочлен і 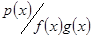 і
і 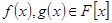 , тоді або
, тоді або 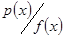 або
або 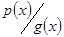 .
.
(Доведення)
Припустимо 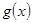 не ділиться на
не ділиться на 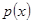 і покажемо
і покажемо 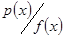 . Доведемо від супротивного, що многочлени
. Доведемо від супротивного, що многочлени 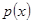 і
і 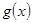 взаємнопрості.
взаємнопрості. 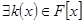 такий, що ст
такий, що ст 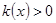
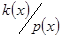 ,
, 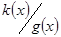 , тоді з незвідності многочлена
, тоді з незвідності многочлена 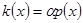 , де
, де 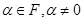 , тобта
, тобта 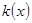 і
і 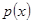 асоціативні. Оскільки
асоціативні. Оскільки 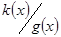 , то і для асоційовного виконується
, то і для асоційовного виконується 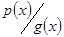 . Прийшли до суперечності Таким чином
. Прийшли до суперечності Таким чином 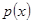 і
і 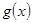 - взаємнопрості і за наслідком з теореми про НСД
- взаємнопрості і за наслідком з теореми про НСД 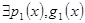 такі, що
такі, що 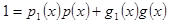 . Домножимо цю рівність на
. Домножимо цю рівність на  маємо:
маємо:
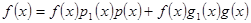 .
.
Зрозуміло, що 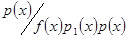 за умовою, тоді
за умовою, тоді 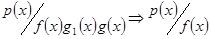 .
.
Зауваження 1.
Індукцією по числу многочленів можна довести наступне твердження. Нехай 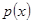 незвідний многочлен
незвідний многочлен 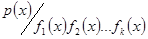 , де
, де 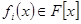
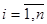 , тоді хоч для одного номера
, тоді хоч для одного номера 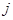
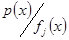 .
.
Зауваження 2.
Доведена лема виконується тільки якщо 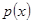 незвідний многочлен. Справді, нехай
незвідний многочлен. Справді, нехай 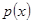 звідний многочлен, тоді існують такі многочлени, що
звідний многочлен, тоді існують такі многочлени, що 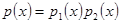 і степені цих многочленів більші нуля.
і степені цих многочленів більші нуля.
ст 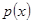 =ст
=ст 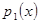 +ст
+ст 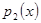 тобто ст
тобто ст 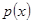 >ст
>ст 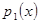 , ст
, ст 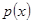 >ст
>ст 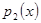 ,
,
а тому жодлен із многочленів 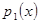 ,
, 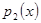 не ділиться на
не ділиться на 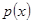 . Прийшли до суперечності.
. Прийшли до суперечності.
№8
Аналогічно основній теоремі арифметики будь-який многочлен відмінний від 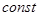 можна розкласти в добуток незвідних многочленів.
можна розкласти в добуток незвідних многочленів.
Нехай 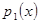 ,
, 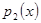 незвідні многочлени
незвідні многочлени 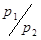 . Припускаємо, що многочлени мають степінь більшу нуля. Тоді
. Припускаємо, що многочлени мають степінь більшу нуля. Тоді 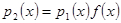 , де
, де 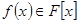 . За означенням незвідного многочлена ст
. За означенням незвідного многочлена ст 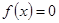 , тобто
, тобто 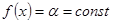 при цьому
при цьому 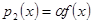 і
і 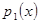 ,
, 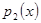 - асоційовні.
- асоційовні.
№9
Лема про похідну
Означення.
Множник 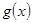 входить множником в многочлен
входить множником в многочлен  з кратністю
з кратністю 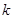 , якщо
, якщо  ділиться на
ділиться на 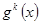 і не ділиться на
і не ділиться на 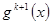 .
.
Означення.
Похідною многочлена 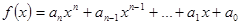 степеня більше одиниці назвемо многочлен вигляду
степеня більше одиниці назвемо многочлен вигляду 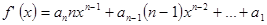 . Похідною многочлена нульового степеня вважається нульовий многочлен.
. Похідною многочлена нульового степеня вважається нульовий многочлен.
Це алгебраїчне означення похідної співпадає з функціональним. Безпосередньо перевіряються наступні умови:
1.  ;
;
2. 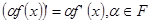 ;
;
3. 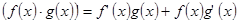 ;
;
4. 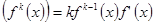 .
.
Лема.
Якщо незвідний многочлен 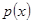 входить множником до многочлена
входить множником до многочлена  з кратність
з кратність 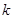 то
то 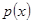 входить до
входить до  з кратністю
з кратністю 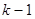 .
.
(Доведення)
За умовою 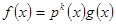 , де ногочлен
, де ногочлен 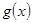 не ділиться на
не ділиться на 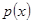 . Знайдемо похідну
. Знайдемо похідну 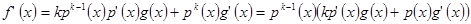 . Зрозуміло, що
. Зрозуміло, що 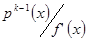 і залишається показати, що
і залишається показати, що 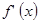 не ділиться на
не ділиться на 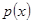 . За умовою леми, це означає
. За умовою леми, це означає 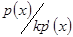 , але ст
, але ст 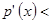 ст
ст 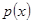 . Прийшли до суперечності.
. Прийшли до суперечності.
Наслідок 1
Якщо незвідний многочлен 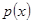 входить до многочлена
входить до многочлена  з кратністю 1 то
з кратністю 1 то 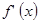 не ділиться на
не ділиться на 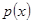 .
.
Наслідок 2
Якщо 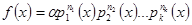 канонічний розклад многочлена
канонічний розклад многочлена  в добуток незвідних многочленів то НСД
в добуток незвідних многочленів то НСД 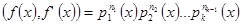 .
.
Наслідок 3
Всі незвідні многочлени входять до канонічного розкладу  з кратністю 1 тоді, і тільки тоді коли многочлени
з кратністю 1 тоді, і тільки тоді коли многочлени  і
і 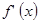 взаємнопрості.
взаємнопрості.
Кратність коренів многочленів
Нехай 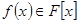 деякий многочлен. Якщо
деякий многочлен. Якщо 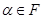 є коренем цього многочлена, то за теоремою Безу
є коренем цього многочлена, то за теоремою Безу 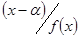 . Корінь
. Корінь 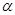 ненульового многочлена
ненульового многочлена  коренем кратності
коренем кратності 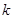 якщо
якщо  ділиться на
ділиться на 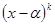 і не ділиться на
і не ділиться на 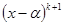 .
.
Корінь кратності 1 називається простим коренем, корінь степінь якого більше 1 називається кратним коренем.
Лема.
Число коренів даного многочлена з урахуванням їх кратності не перевищує степеня даного многочлена.
(Доведення)
Припустимо 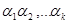 корені многочлена
корені многочлена  кратності відповідно
кратності відповідно 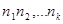 . Це означає, що многочлен
. Це означає, що многочлен  ділиться на
ділиться на 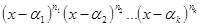 , але всі многочлени
, але всі многочлени 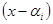 незвідні, тобто взаємнопрості, а тому
незвідні, тобто взаємнопрості, а тому  ділиться на добуток многочленів
ділиться на добуток многочленів 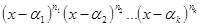 , тобто
, тобто 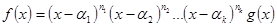 . Тоді ст
. Тоді ст 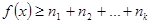 .
.
№10
Теорема.
Незвідними над полем 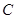 є всі многочлени 1-го степеня і лише вони.
є всі многочлени 1-го степеня і лише вони.
(Доведення)
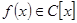 якщо степінь
якщо степінь  дорівнює 1, то многочлен незвідний, якщож степінь більший 1 то за наслідком многочлен можна розкласти в добуток многочленів 1-го степеня і
дорівнює 1, то многочлен незвідний, якщож степінь більший 1 то за наслідком многочлен можна розкласти в добуток многочленів 1-го степеня і  - звідний.
- звідний.
Незвідні многочлени над плем дійсних чисел
Визначимо деякі типи незвідних многочленів над полем 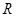 . Припустимо
. Припустимо 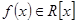 степеня 1. Такий многочлен незвідний.
степеня 1. Такий многочлен незвідний.
Припустимо степінь  рівний 2 і многочлен не має дійсних коренів – незвідний над
рівний 2 і многочлен не має дійсних коренів – незвідний над 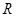 .
.
Інших незвідних многочленів над полем 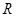 не існує.
не існує.
Лема.
Нехай  многочлен з дійсними коефіцієнтами степеня більшого 2-х.
многочлен з дійсними коефіцієнтами степеня більшого 2-х. 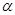 комплексний корінь многочлена
комплексний корінь многочлена  , тоді
, тоді 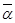 теж корінь многочлена
теж корінь многочлена  .
.
(Доведення)
Доведемо деякі властивості комплексноспряжених чисел:
1. 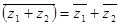 ;
;
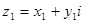 ,
, 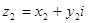
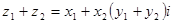
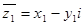 ,
, 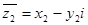
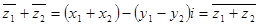
2. 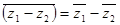 (аналогічно)
(аналогічно)
3. 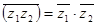
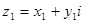 ,
, 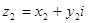
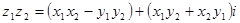
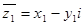 ,
, 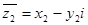
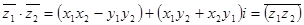
4. 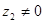
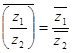
Доведемо твердження леми 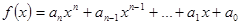 , де
, де 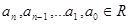
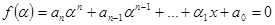 за умовою
за умовою 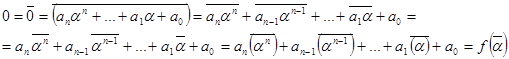 і
і 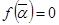 .
.
№11
Звідні многочлени на полі раціональних чисел
Будемо розв’язувати задачу пошуком раціональних коренів многочлена з раціональними коефіцієнтами. 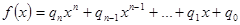 , де
, де 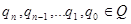 домножимо многочлен
домножимо многочлен  на
на 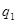 при цьому корені многочлена не змінюються, але ми одержимо многочлен з цілими числами.
при цьому корені многочлена не змінюються, але ми одержимо многочлен з цілими числами.
Задача пошуку раціональних коренів многочлена з раціональними коефіцієнтами зводиться до пошуку раціональних коренів многочлена з цілими коефіцієнтами.
Теорема.
Нехай нескоротиий дріб 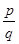 є коренем многочлена з цілими коефіцієнтами
є коренем многочлена з цілими коефіцієнтами 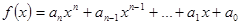 , де
, де 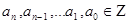 , тоді
, тоді
1. 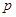 дільник
дільник 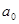 ;
;
2. 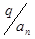 ;
;
3. 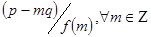
(Доведення)
За умовою 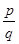 корінь многочлена
корінь многочлена  , тобто
, тобто 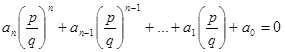 . Домножимо даний вираз на
. Домножимо даний вираз на 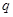 маємо
маємо 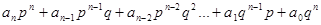 (1)
(1)
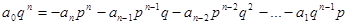 . Всі доданки в правій частин і містять
. Всі доданки в правій частин і містять 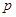 , а тому
, а тому 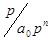 . Дріб
. Дріб 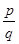 нескоротний дріб, тому
нескоротний дріб, тому 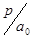 і
і 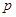 ,
, 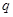 взаємнопрості числа.
взаємнопрості числа.
З рівняння (1) рдержимо 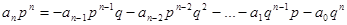 всі доданки вправій частині діляться на
всі доданки вправій частині діляться на 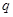 , тому
, тому 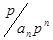 і оскільки
і оскільки 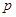 ,
, 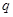 взаємнопрості числа, то
взаємнопрості числа, то 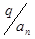 .
.
Перепишемо рівність (1) у вигляді 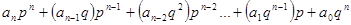 . Нехай
. Нехай 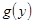 многочлен вигляду
многочлен вигляду 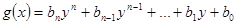 , де
, де 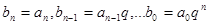 тоді многочлен
тоді многочлен 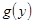 з цілими коефіцієнтами і з рівності (1) випливає, що
з цілими коефіцієнтами і з рівності (1) випливає, що 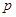 число цього ногочлена. За теоремою Безу
число цього ногочлена. За теоремою Безу 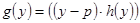 , де
, де 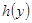 многочлен з цілими коефіцієнтами, які можна знайти за схемою горнера. Тоді
многочлен з цілими коефіцієнтами, які можна знайти за схемою горнера. Тоді 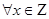
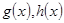 цілі числа, а тому
цілі числа, а тому 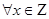
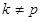
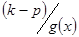 . Припустимо
. Припустимо 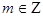 оскільки
оскільки 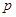 ,
, 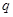 взаємнопрості числа, то
взаємнопрості числа, то 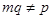 і
і 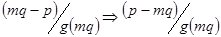 .
.
Якщо 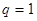 , то вибераємо
, то вибераємо 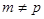 , тоді
, тоді 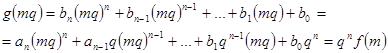 і
і
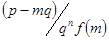 . Покажемо, що числа
. Покажемо, що числа 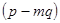 і
і 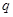 взаємнопрості. Припустимо
взаємнопрості. Припустимо 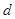 спільний дільник. Тоді
спільний дільник. Тоді
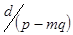 і
і 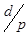 , але числа
, але числа 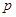 ,
, 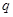 взаємнопрості, тому
взаємнопрості, тому 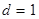 . Остаточно
. Остаточно 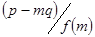 .
.
№12
№13
В алгебре
В алгебре примитивный многочлен — это всякий многочлен 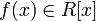 , где R — ассоциативно-коммутативное кольцо с однозначным разложением на множители, коэффициенты которого не имеют нетривиальных общих делителей.
, где R — ассоциативно-коммутативное кольцо с однозначным разложением на множители, коэффициенты которого не имеют нетривиальных общих делителей.
