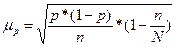Показатели вариации (колеблемости) признака

Среднее линейное отклонение – на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.

-для несгруппированных данных (первичного ряда):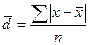

-для вариационного ряда: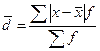

Среднее квадратическое отклонение

- для несгруппированных данных: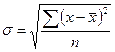

- для вариационного ряда: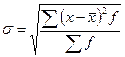

Дисперсия

- для несгруппированных данных: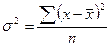

- для вариационного ряда: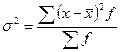

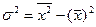
Коэффициент вариации (используется для характеристики однородности совокупности по исследуемому признаку)

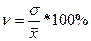- до 17% – совокупность совершенно однородна, 17%-33% - достаточно однородна, >33% - неоднородна.

Сложение дисперсий

Величина общей дисперсии ( 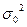) характеризует вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности

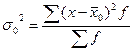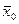, - общая средняя арифметическая для всей совокупности

Межгрупповая дисперсия ( 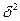) отражает систематическую вариацию, т. е. различия в величине изучаемого признака, которые возникают под влиянием фактора, положенного в основу группировки

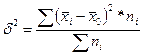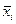, - средняя в каждой группе, 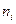- число единиц в каждой группе

Средняя внутригрупповая дисперсия ( 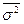) характеризует случайную вариацию, возникающую под влиянием других, неучтенных факторов, и не зависит от условия (признака-фактора), положенного в основу группировки.

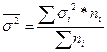, где 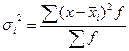- дисперсия по отдельной группе

или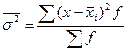

Равенство: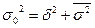

Корреляционное отношение

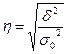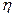, >0,5 – связь между групповым фактором и результирующим признаком – тесная, 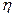<0,5 – связь слабая

Показатель асимметрии

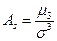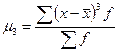, - центральный момент третьего порядка

Средняя квадратическая ошибка: 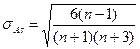, n – число наблюдений

Если 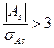, асимметрия существенна и распределение признака в генеральной совокупности не является симметричным. Если 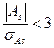, асимметрия несущественна, ее наличие объясняется влиянием случайных обстоятельств.

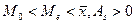- правосторонняя асимметрия, 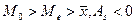- левосторонняя асимметрия.

Показатель эксцесса (островершинности)

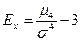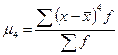, - центральный момент четвертого порядка

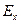>0 – высоковершинное, 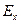< 0 – низковершинное ( 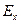= -2 – предел)

Средняя квадратическая ошибка: 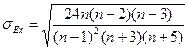n – число наблюдений

Кривые распределения

Кривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения.

Плотность распределения (расчет теоретических частот)

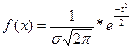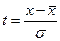, - нормированное отклонение

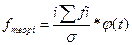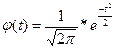, - определяется по таблице (приложение 1)

Критерий согласия К. Пирсона (для проверки близости теоретического и эмпирического распределений, для проверки соответствия эмпирического распределения закону нормального распределения)

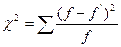f – эмпирические частоты в интервале, f^’ – теоретические частоты в интервале

Критерий согласия Романовского

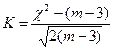, m – число групп, m-3 – число степеней свободы при исчислении частот нормального распределения

Если к<3, то можно принять гипотезу о нормальном характере эмпирического распределения

Критерий Колмогорова

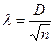, D – максимальное значение разности между накопленными эмпирическими и теоретическими частотами, n – сумма эмпирических частот

Распределение Пуассона (теоретические частоты)

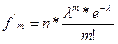, n – общее число независимых испытаний, λ – среднее число появления редкого события в n одинаковых независимых испытаниях, m – частота данного события, е=2,71828

Выборочное наблюдение

N – объем генеральной совокупности

n – объем выборочной совокупности (число единиц, попавших в выборку)

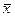- генеральная средняя (среднее значение признака в генеральной совокупности)

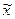- выборочная средняя

р – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности)

w – выборочная доля

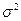- генеральная дисперсия

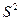- выборочная дисперсия

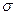- среднее квадратическое отклонение признака в генеральной совокупности

S – среднее квадратическое отклонение признака в выборочной совокупности.

Неравенство Чебышеба

При неограниченном числе наблюдений, независящих друг от друга из генеральной совокупности с вероятностью сколь угодно близкой к 1, можно утверждать, что расхождение между выборочной и генеральной средней будет сколь угодно малой величиной .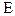

Теорема Ляпунова

Дает количественную оценку ошибки. При неограниченном объеме из генеральной совокупности с Р расхождения выборочной и генеральной средней равна интегралу Лапласа

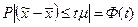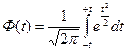, - нормированная функция Лапласа (интеграл Лапласа)

Р – гарантированная вероятность

t – коэффициент доверия, зависящий от Р

Р	0,683	0,954	0,997
t

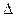- предельная ошибка выборки

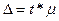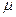, - стандартная среднеквадратическая ошибка

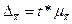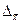, - предельная (максимально возможная) ошибка средней, t – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки

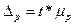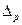, - предельная (максимально возможная) ошибка доли

Средняя ошибка (n>30) при случайной повторной выборке:

,

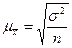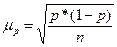
При случайной бесповторной выборке:

,
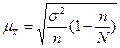