Центральные проекции и их основные свойства.

При центральном проецировании (по­строении центральных проекций) задают плоскость проекций и центр проекций – точку, не лежащую в плоскости проекций. На рисунке 1.1 плоскость P – плоскость проекций, точка S – центр проекций.

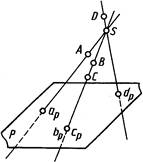
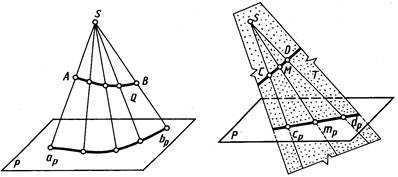
Рис. 1.1 Рис. 1.2 Рис. 1.3

Для проецирования произвольной точки через нее и центр проекций проводят прямую. Точка пе­ресечения этой прямой с плоскостью проекций и является центральной про­екцией заданной точки на выбранной плоскости проекций.

На рисунке 1.1 центральной проек­цией точки А является точка а_р пересе­чения прямой SA с плоскостью Р. Так же построены центральные проекции b_p , c_p , d_p точек В, С, D на плоскости Р.

Прямые, проходящие через центр проекций и проецируемые точки, называют проецирующими прямыми.

Центральные проекции b_p и c_p двух различных точек В и С в пространстве, которые располагаются на одной проецирующей прямой, совпадают. Все множество точек пространства, при­надлежащих одной проецирующей прямой, имеет при одном цен­тре проецирования одну центральную проекцию на заданной плоскости проекций.

Следовательно, при заданных плоскости проекций и центре проецирования одна точка в пространстве имеет одну централь­ную проекцию. Но одна центральная проекция точки не позволяет однозначно определить положение точки в пространстве.

Для обеспечения обратимости чертежа, т. е. однозначного определения положения точки в пространстве по ее проекции, нужны дополнительные условия, например, можно задать второй центр проекций. Центральным проецированием может быть построена проекция любой линии или поверхности как мно­жество проекций всех ее точек (рис.1.2 и рис.1.3). При этом проецирующие прямые (в своей совокупности), проведенные через все точки кривой линии, образуют проецирующую ко­ническую поверхность (рис.1.2) или могут оказаться в одной плоскости (рис.1.3), которая называется проецирующей.

Проекция кривой линии представляет собой линию пересече­ния проецирующей конической поверхности с плоскостью про­екций. Так, на рисунке 1.2 проецирующая коническая поверхность Q пересекается с плоскостью проекций P по кривой а_р b_р, являю­щейся проекцией линии AB. Однако проекция линии не опреде­ляет проецируемую линию, так как на проецирующей поверхности может быть бесчисленное количество линий, проецирующихся в одну и ту же линию на плоскости проекций (рис. 1.4).

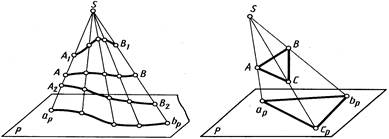
Рис. 1.4 Рис. 1.5

При проецировании прямой линии, не проходящей через центр проекций, проецирующей поверхностью служит плос­кость. Так, на рисунке 1.3 проецирующая плоскость T, обра­зуемая проецирующими прямыми SC и SD, проходящими через точки С и D прямой, пересекает плоскость проекций P по пря­мой c_p d_p,которая и является проекцией прямой CD.Соответ­ственно проекция m_p точки M прямой CD принадлежит и проекции c_p d_p .

Для построения проекций линий, поверхностей или тел ча­сто достаточно построить проекции лишь некоторых характер­ных точек. Например, при построении на плоскости проекций P проекции треугольника ABC (рис.1.5) достаточно построить проекции а_р, b_р,, с_р трех его точек – вершин А, В, С.

В центральных проекциях:

– для прямой линии проецирующей поверхностью в общем случае служит плоскость, и поэтому прямая линия вообще проецируется в виде прямой (рис.1.3);

– каждая точка и линия в пространстве имеют единственную свою проекцию;

– каждая точка на плоскости проекций может быть проекцией множества то­чек, если через них проходит общая для них проецирующая прямая (рис.1.1);

– каждая линия на плоскости проекций может быть проекцией множества ли­ний, если они расположены в общей для них проецирующей плоскости (рис.1.4);

– для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции этих точек провести прямую линию;

– если точка принадлежит прямой, то проекция точки принадлежит проекции
этой прямой.

Параллельные проекции.

Параллельное проецирование можно рассматривать как частный случай центрального проецирования, при котором центр проецирования бесконечно удален.

Условимся считать все проецирующие прямые параллельными. Для их проведения должно быть указано некоторое направление (рис.1.6 слева). Построенные таким образом проекции называются параллельными.

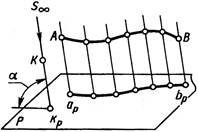
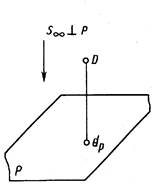
Рис. 1.6 Рис.1.7

Следовательно, параллельной проекцией точки будем называть точку пересече­ния проецирующей прямой, проведенной параллельно заданному направлению, с пло­скостью проекций.

Чтобы получить параллельную проекцию некоторой линии, можно построить проекции ряда ее точек и провести через эти проекции линию (рис.1.6 справа).

При этом проецирующие прямые в своей совокупности образуют цилиндриче­скую поверхность. Поэтому параллельные проекции также называют ци­линдрическими.

Параллельные проекции делятся на косоугольные и прямоугольные или ортогональные. В первом случае направление проецирования составляет с плоскостью проекций угол, не равный 90°; во втором случае проецирующие прямые перпендикулярны к плоскости проекций.

Прямоугольное или ортогональное проецирование это частный случай параллельного проецирования. Прямоугольной (ортогональной) проекцией точки называют основание перпендикуляра, проведенного из точки на плоскость проекций. Прямоугольная проекция d_p точки D по­казана на рисунке 1.7.

При рассмотрении параллельных проекций следовало бы представить себя уда­ленным на бесконечно большое расстояние от изображения. На самом же деле предметы и их изображения рассматриваются с конечного расстояния; при этом лучи, идущие в глаз зрителя, образуют поверхность коническую, а не цилиндриче­скую. Следовательно, более естественное изображение получается (при соблюдении определенных условий) центральным проецированием, а не параллельным. Поэто­му, когда требуется, чтобы изображение давало такое же зрительное впечатление, как и сам предмет, применяют перспективные проекции, в основе которых лежит центральное проецирование.

Но сравнительно большая простота построения и свойства параллельных про­екций, обеспечивающие сохранение натуральных размерных соотношений, объяс­няют широкое применение параллельного проецирования, несмотря на условность, указанную выше.