Связность в неориентированных графах

Определение.Неориентированный граф G связен, если существует хотя бы один маршрут в G между каждой парой вершин i и j.

Определение.Подграфом графа G(V,E) называется граф, все вершины которого принадлежат V(G), а все ребра принадлежат E(G).

Определение.Максимальный связный подграф графа G называется связной компонентой графа G. Замечание: максимальный не в смысле количества ребер, а в смысле нерасширяемости.

Например, на рис. 19 изображен несвязный граф с тремя компонентами связности.

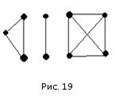
Заметим, что каждая компонента связности неориентированного графа представляет собой неориентированный граф, а значит, для нее выполняется лемма о рукопожатиях.

Связность ориентированных графов

Определение.Ориентированный граф G связен, если неориентированный граф, получающийся из G путем удаления ориентации ребер, является связным.

Определение.Ориентированный граф сильно связен, если для каждой пары вершин i и j существует по крайней мере один путь из i в j и по крайней мере один путь из j в i.

Определение.Максимальный сильно связный подграф орграфа называется сильно связной компонентой.

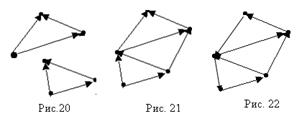
На рис. 20 – 22 изображены несвязный, связный, но не сильно и сильносвязный графы соответственно.

Циклы

Эйлеров цикл

Определение. Эйлеров цикл – цикл, который проходит ровно один раз по каждому ребру (дуге) графа.

Определение.Если граф имеет цикл, содержащий все ребра (дуги) графа по одному разу, то граф называется эйлеровым.

Не все графы имеют эйлеровы циклы, но если эйлеров цикл существует, то это означает, что, следуя вдоль этого цикла, можно нарисовать граф на бумаге, не отрывая от нее карандаша.

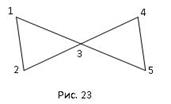
Граф, изображенный на рис. 23, является эйлеровым. Задача о Кенегсбергских мостах, рассмотренная выше, предполагает нахождение эйлерова цикла в мультиграфе.

Теорема. Связный неориентированный граф G содержит эйлеров цикл тогда и только тогда, когда все вершины в нем имеют четную степень.

Доказательство.

1. Докажем прямую теорему.

Пусть граф G содержит эйлеров цикл, значит, существует цикл, проходящий по всем ребрам графа ровно по одному разу. Будем идти по циклу и считать степени вершин. Т.к. проходя через вершину каждый раз, прибавляем к её степени 2, то степени всех вершин четны.

2. Докажем обратную теорему (способ доказательства – конструктивный, то есть дает алгоритм построения эйлерова цикла).

Пусть все вершины графа имеют четную степень. Будем строить эйлеров цикл, начиная с некоторой вершины v₀, при этом пройденные ребра будем удалять. Так как все вершины имеют четную степень, то, попав в какую-либо вершину, обязательно найдем ребро, по которому можно из неё выйти. Таким образом, обязательно вернемся в вершину v₀, получив при этом некоторый цикл Р. Если при этом все ребра графа участвуют в цикле, то теорема доказана.

В противном случае, так как граф связен, обязательно найдется ребро, не входящее в цикл, но инцидентное какой-либо вершине цикла. Обозначим эту вершину v₁. Будем строить цикл, начиная с вершины v₁. Из аналогичных соображений мы обязательно вернемся в вершину v₁, получив цикл Р1. Если при этом все ребра графа присутствуют в циклах Р и Р1, то цикл v₁Рv₁Р1v₁ содержит все ребра графа по одному разу, то есть является эйлеровым, следовательно, теорема доказана. В противном случае продолжаем аналогичные рассуждения. Так как ребер в графе конечное количество, построение цикла обязательно закончится.

Теорема. Связный орграф является эйлеровым тогда и только тогда, когда полустепень исхода каждой вершины равна полустепени ее захода.

Доказательствоаналогично случаю неориентированного графа.

Гамильтонов цикл

Определение.Граф называется гамильтоновым, если в нем имеется цикл, содержащий каждую вершину этого графа.

Уильям Роуэн Гамильтон выпустил головоломку, суть которой состояла в построении пути, который через каждую вершину проходит по одному разу. Задача похожа на задачу о нахождении эйлеровой линии, однако до сих пор не найдены необходимые и достаточные условия существования в графе гамильтоновых линий.

Похожа на данную и задача о коммивояжере, которая тоже состоит в построении цикла, проходящего по всем городам по одному разу, но при этом требуется минимизировать транспортные расходы. Алгоритма решения данной задачи тоже не существует.

Некоторые головоломки типа как перевезти волка, козу и капусту тоже сводятся к поиску гамильтоновой линии на некотором графе, изображающем все возможные перевозки. Известна также задача о нахождении пути коня на шахматной доске, при котором он побывает на каждом поле по одному разу (вариант – и вернется на исходное поле последним ходом), которая тоже является частным случаем задачи о нахождении гамильтоновой линии.

Например, на рис. 18 и 22 изображены гамильтоновы графы, а на рис. 21 и 23 – графы, не являющиеся гамильтоновыми.

Турниры

Определение.Граф называется полугамильтоновым, если существует маршрут, содержащий каждую его вершину ровно один раз.

Определение.Турнир (полный ориентированный граф) – орграф, в котором любые его две вершины соединены ровно одной дугой.

Этот класс графов получил свое название в связи со спортивными турнирами без ничьих, проводимых по круговой системе. Результаты встреч можно описать орграфом, вершины которого соответствуют участникам соревнований, а дуга (v ,w) есть в графе, если участник, соответствующий вершине v, выиграл у участника, соответствующего вершине w.

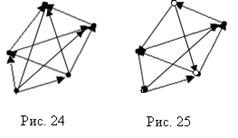
На рис. 24 изображен не сильносвязный турнир, а на рис. 25 – сильносвязный.

Теорема. Любой турнир полугамильтонов.

Доказательство (метод математической индукции по количеству вершин). Если турнир имеет меньше четырех вершин, то утверждение, очевидно, верно. Проведем индукцию по числу вершин. Предположим, что любой турнир с n вершинами полугамильтонов. Пусть Т — турнир с n+1 вершинами, и пусть турнир Т’ с n вершинами получен из Т удалением некоторой вершины О вместе со всеми инцидентными ей дугами. Тогда по предположению индукции Т’ обладает полугамильтоновым маршрутом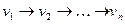

Рассмотрим три случая.

(1) Если {v, v₁) — дуга в T, то искомой простой орцепью является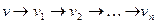

(2) Если (v, v₁) не является дугой в Т (это означает, что дугой является (v₁, v)), и если существует такое i, что (v, v_i) – дуга в T, то, выбирая первое i с таким свойством (см. рис. 26), получим, что искомым маршрутом является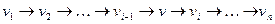

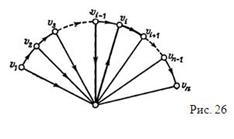
(3) Если в Т не существует дуги вида (v,v_i), то искомым маршрутом является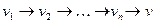

Теорема. Любой сильно связный турнир гамильтонов.

Доказательство (метод математической индукции по длине цикла). Докажем более сильный результат, состоящий в том, что сильно связный турнир Т с n вершинами содержит циклы длины 3, 4, … n.

Докажем, что существует цикл длины три. Пусть Т – сильно связный турнир. Тогда для любой вершины v из Т все множество дуг, ей инцидентных, можно разделить на два не пересекающихся подмножества W – множество дуг, для которых вершина v является концом, и Z – множество дуг, для которых вершина v является началом. Так как Т сильно связен, то оба этих множества не пусты, следовательно, найдутся вершины w, принадлежащая W, и z, принадлежащая Z, тогда имеем цикл v, w , z, v длины три.

Предположим, что существуют циклы длины меньшей или равной k – v₁, v₂, …,v_k. Докажем, что существует цикл длины k. Возможны два случая:

1. Существует вершина v, у которой есть инцидентные дуги, направленные к циклу и направленные из цикла. Тогда находим первую дугу, направленную к циклу, пусть это будет дуга (v, vi). Тогда искомый цикл имеет вид: v₁, v₂, …v_i-1, v, v_i,…,v_k.

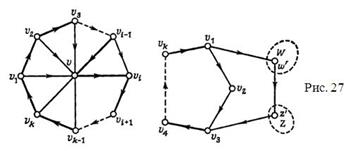
2. Для любой вершины графа все дуги направлены либо к циклу, либо из цикла. Тогда все множество вершин, не входящих в цикл, можно разделить на два непересекающихся подмножества W – множество вершин, у которых все дуги направлены к циклу, и Z – множество вершин, у которых все дуги направлены из цикла. Так как Т сильно связен, то оба этих множества не пусты, следовательно, найдутся вершины w’, принадлежащая W, и z’, принадлежащая Z, тогда имеем цикл v₁, w',z',v₃, …,v_k длины k+1 (см. рис. 27).

Деревья

Определение. Лесом называют граф без циклов.

Определение. Деревом называют произвольный связный граф без циклов.

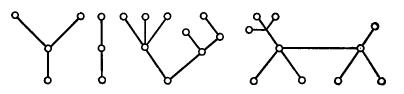
Таким образом, лесом называетсянесвязныйграф, представляющийобъединениедеревьев. На рис. 28, представленном ниже, изображен лес с четырьмя компонентами связности, каждая из которых представляет собой дерево.

Рис. 28

Рис.28

Удобно считать, что граф, состоящий из одной изолированной вершины, тоже является деревом.

Определение. Вершина дерева, степень которой равна единице, называется висячей вершиной или листом.

Свойства деревьев

1. Граф является деревом тогда и только тогда, когда каждая пара вершин в нем соединена одной и только одной простой цепью.

2. Удаление всякого ребра в дереве приводит к увеличению числа компонент связности.

3. Дерево с p вершинами всегда имеет (p-1) ребер.

4. Если G – лес, р вершин и k компонент связности, то G имеет р-к ребер.

5. В каждом дереве существует по крайней мере две висячие вершины.

Доказательство свойств деревьев предлагается читателю в качестве упражнений.

Определение. Для произвольного связного неориентированного графа G(V,E) каждое дерево Т(V₁,T₁), где V₁=V и Е₁ÍE называют стягивающим деревом (каркасом, остовом). Ребра такого дерева называют ветвями, а остальные ребра графа – хордами.

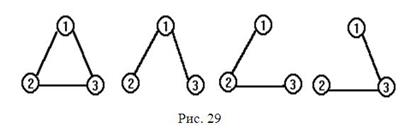
На рис. 29 приведен пример графа и его каркасов.

Рис. 29

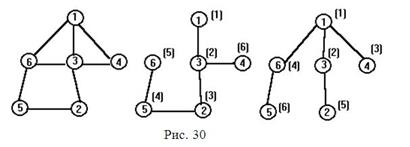
На рис. 30 представлены граф и его каркасы, построенные методами поиска в глубину и в ширину. В круглых скобках указана очередность просмотра вершин графа при соответствующем поиске.

Планарные графы

Во многих случаях не имеет значения, как изобразить граф, т.к. изоморфные графы несут одну и ту же информацию. Но встречаются ситуации, когда важно выяснить, возможно ли нарисовать граф на плоскости так, чтобы его изображение удовлетворяло определенным требованиям. Например, в радиоэлектронике при изготовлении микросхем печатным способом электрические цепи наносятся на плоскую поверхность изоляционного материала. Так как проводники не изолированы, то они не должны пересекаться. Аналогичная задача возникает при прокладке железнодорожных и других путей, где не желательны переезды.

Определение.Плоским называется граф, изображенный на плоскости так, что никакие два ребра геометрически не пересекаются нигде, кроме инцидентных им обоим вершин.

Определение. Граф, изоморфный плоскому, называется планарным.

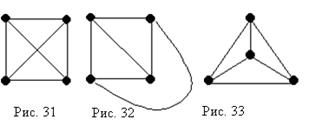
Граф К₄ (рис. 31) – планарен, ему соответствуют плоские графы, изображенные на рис. 32 и 33.

Определение.Область, ограниченная ребрами в плоском графе и не содержащая внутри себя вершин и ребер, называется гранью.

Ниже на рис. 34 изображен граф с четырьмя гранями.

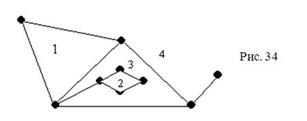
Заметим, что грань 4 не ограничена, такую грань называют внешней, все остальные грани называют внутренними.

Теорема (Формула Эйлера).Пусть G – связный планарный граф. Тогда справедливо следующее равенство p–q+r=2, где p – количество вершин, q – количество ребер, r – количество граней.

Доказательство (методом математической индукции по количеству ребер). При q=0 теорема верна. Очевидно, что если q=0, то p=1 и r=1, тогда p–q+r=2.

Пусть теорема верна для всех графов с q ребрами: p–q+r=2. Добавим еще одно ребро. Если добавляемое ребро соединяет существующие вершины, то q1=q+1, p1=p, r1=r+1 и p1–q1+r1=p–(q+1)+r+1= p–q+r=2. Если добавляемое ребро соединяет существующую вершину с новой, то q1=q+1, p1=p+1, r1=r и p1–q1+r1=p+1–(q+1)+r= p–q+r=2.

Теорема.Если G – связный планарный граф с р вершинами и q ребрами и p>3, то q£3p–6.

Доказательство.Так как каждая грань ограничена, по крайней мере, тремя ребрами, каждое ребро ограничивает не более двух граней, то 3r£2q. Из формулы Эйлера следует, что 2=p–q+r, тогда 2£p–q+²/₃q, следовательно, 3p–3q+2q³6, тогда q£3p–6.

Теорема.Граф К₅ не является планарным.

Доказательство.Предположим противное, граф планарен. Тогда p=5, q=4*5/2=10, по формуле Эйлера r=7. Тогда не выполняется условие предыдущей теоремы q£3p–6, а значит, наше предположение не верно – граф не является планарным.

Теорема.Граф К_{3, 3} не является планарным.

Доказательство.Предположим противное, граф является планарным. Тогда p=6, q=9, по формуле Эйлера r=5. В данном графе нет треугольников, следовательно, если он планарен, то в его плоской укладке каждая грань ограничена по крайней мере 4 ребрами. Таким образом, 4r£2q, 2r£q. Но полученное условие для нашего графа не выполняется, а значит, наше предположение не верно – граф не является планарным.

Теорема.В планарном графе существует вершина степени не больше пяти.

Доказательство.Предположим противное, степень любой вершины графа не менее шести. Тогда сумма степеней всех вершин не менее 6*р, следовательно, по лемме о рукопожатиях 2q³6p, отсюда p£q/3. Так как q£3p–6, получим q£q–6. Таким образом, получили противоречие, значит, наше предположение не верно, в планарном графе обязательно должна быть вершина, степень которой меньше шести.

Определение. Элементарным стягиванием называется следующая процедура: берем ребро е (вместе с инцидентными ему вершинами u, v) и «стягиваем» его, то есть удаляем е и отождествляем вершины u и v; полученная при этом вершина инцидентна тем ребрам (отличным от е), которым первоначально были инцидентны вершины u и v.

Ниже на рис. 35 представлены два графа: до и после процедуры элементарного стягивания ребра е.

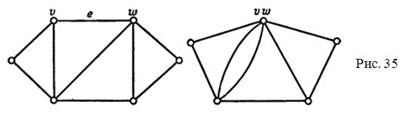
Определение. Граф G называется стягиваемым к графу H, если Н можно получить из G с помощью некоторой последовательности элементарных стягиваний.

Теорема Куратовского.Граф является планарным тогда и только тогда, когда в нем нет подграфов, стягиваемых к графам К₅ или К_3,3.

Раскрашивание графов

Определение. Произвольная функция f:V®{1,2,...,k}, где k принадлежит множеству натуральных чисел, называется вершинной k-раскраской графа G(V,E).

Определение.Раскраска называется правильной, если f(u)¹f(v) для любых смежных вершин u и v.

Определение.Граф, для которого существует правильная k-раскраска, называется k-раскрашиваемым.

Определение.Минимальное число k, при котором граф G является k-раскрашиваемым, называется хроматическим числом графа и обозначается c(G).

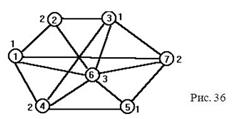
Для графа на рис. 36 c(G)=3. Меньшим количеством цветов граф правильно раскрасить нельзя из-за наличия подграфов К₃. Рядом с вершинами графа указаны номера цветов.

Раскраска планарных графов

Проблема раскраски планарных графов является одной из самых известных проблем теории графов. Первоначально вопрос формулируется следующим образом: достаточно ли четырех красок для такой раскраски произвольной географической карты, при которой соседние страны окрашены в различные цвета? В 1879 г. британский математик А. Кэли выдвинул гипотезу четырех красок: «Всякий планарный граф вершинно 4-раскрашиваем».

Гипотеза четырех красок привлекала внимание многих исследователей. Уже в 1880 г. появилось первое доказательство А. Кемпе. Ошибка в этом доказательстве была обнаружена Р. Хитвудом в 1890 г. Одновременно он показал, что если в формулировке гипотезы слово «четыре» заменить на «пять», то полученная теорема легко доказывается.

Теорема о пяти красках.Всякий планарный граф 5-раскрашиваем.

Доказательство (метод математической индукции по количеству вершин). Для планарных графов, у которых меньше шести вершин, теорема очевидна.

Предположим, что G планарный граф с n вершинами и что все планарные графы с n-1 вершинами 5-раскрашиваемы. Можно считать, что G плоский граф и что он содержит вершину v, степень которой не больше пяти. Удаление вершины v и всех инцидентных ей ребер приводит нас к графу с n-1 вершиной, который, по предположению индукции, 5-раскрашиваем, раскрасим его. Тогда в исходном графе G останется окрасить только одну вершину v.

Если степень вершины v меньше пяти, то ее можно окрасить в любой цвет, не участвующий в окраске смежных с ней вершин.

Пусть степень вершины v равна пяти. Если среди смежных вершин есть две вершины одинакового цвета, то ее можно окрасить в цвет, не использованный для окраски этих вершин.

Итак, остался последний случай: всем вершинам, смежным с v, присвоены различные цвета. Обозначим вершины, смежные с v, через v1,v2,...,v5. Пусть они окрашены в цвета c1, c2, ..., c5. Определим H(i,j) как подграф графа G, вершинами которого являются все вершины цвета ci или cj, а ребрами – все ребра, соединяющие вершину цвета ci с вершиной цвета cj. Рассмотрим два случая.

1) v1 и v3 не принадлежат одной компоненте связности графа H(1,3). В этом случае можно поменять цвета всех вершин той компоненты H(1,3), которая содержит v1 (цвет с1 на цвет с3, а цвет с3 на цвет с1). В результате v1 приобретет цвет c3, что позволит окрасить v в цвет c1.

2) v1 и v3 принадлежат одной компоненте связности графа H(1,3). В этом случае существует цикл C вида v->v1->..->v3->v, часть которого, заключенная между v1 и v3 целиком лежит в H(1,3). Так как v2 находится внутри цикла C, а v4 – вне его, то не существует простой цепи из v2 в v4, целиком лежащей в H(2,4). Поэтому v2 и v4 принадлежат разным компонентам связности графа H(2,4). В этом случае можно поменять цвета всех вершин той компоненты H(2,4), которая содержит v2 (цвет с2 на цвет с4, а цвет с4 на цвет с2). В результате v2 приобретет цвет c4, что позволит окрасить v в цвет c2.

Таким образом, все вершины исходного графа можно окрасить в 5 цветов, что и требовалось доказать.