Понятие адаптивной модели

Адаптивные методы могут применяться для прогнозирования показателей фондового рынка, денежных потоков, изменений ежедневных остатков на складах, в инструментальных кладовых, магазинах. С помощью этих же методов удается описать эволюцию изменения технико-экономических характеристик изделий и переменных параметров химических процессов, изучить поведение показателя частоты отказов оборудования в зависимости от его возраста. Наконец, названные методы полезны при анализе сезонных явлений. В ряде случаев эти методы могут с успехом применяться для прогнозирования макропоказателей. Методы адаптивного прогнозирования применяются там, где основной информацией для прогноза являются временные ряды.

Инструментом прогноза при адаптивном методе служит модель. Первоначальная оценка параметров этой модели основывается на данных базового (исходного) временного ряда. На основе новых данных, получаемых на каждом следующем шаге, происходит корректировка параметров модели во времени, их адаптация к новым, непрерывно изменяющимся условиям развития явления. Таким образом, модель постоянно «впитывает» новую информацию и приспосабливается к ней.

Рассматриваемые методы обладают следующими свойствами:

• они применимы для широкого круга задач;

• адаптивное прогнозирование не требует большого объема информации, оно базируется на интенсивном анализе информации, содержащейся в отдельных временных рядах;

• модель, описывающая структуру показателя и его динамику, как правило, отличается ясностью и простотой математической формулировки;

• неоднородность временных рядов и их связей находит отражение в адаптивной эволюции параметров или даже структуры моделей.

Адаптивные методы пригодны лишь для обработки рядов с умеренными изменениями во времени. Они оказываются весьма грубыми при прогнозировании на большое число шагов вперед.

Отличие адаптивных моделей от других прогностических моделей состоит в том, что они отражают текущие свойства ряда и способны непрерывно учитывать эволюцию динамических характеристик изучаемых процессов.

Цель адаптивных методов заключается в построении самокорректирующихся (самонастраивающихся) экономико-математических моделей, которые способны отражать изменяющиеся во времени условия, учитывать информационную ценность различных членов временной последовательности и давать достаточно точные оценки будущих членов данного ряда. Именно поэтому такие модели предназначаются, прежде всего, для краткосрочного прогнозирования.

Основным средством анализа и прогноза временного ряда будет модель. Понятие модель используется в двух значениях: как модель временного ряда, выражающая закон генерирования членов ряда, и как прогнозная модель, или предиктор. Главное отличие этих двух типов моделей в том, что на выходе модели временного ряда фактические члены ряда, а на выходе прогнозной модели — оценки будущих членов ряда. Теоретически свойства предиктора исследуются в предположении, что он применен для получения прогнозов некоего процесса, генерируемого моделью, заданной аналитически.

На временной ряд воздействуют в разное время различные факторы. Одни из них по тем или иным причинам ослабляют свое влияние, другие воздействуют активнее. Таким образом, реальный процесс протекает в изменяющихся условиях, составляющих его внешнюю среду, к которой он приспосабливается, адаптируется. А модель, в свою очередь, адаптируется к ряду, представляющему этот процесс.

Временной ряд — это множество наблюдений, получаемых последовательно во времени. Если время изменяется дискретно, временной ряд называется дискретным.

Мы будем рассматривать только дискретные временные ряды, в которых наблюдения делаются через фиксированный интервал времени, принимаемый за единицу счета. Переход от момента одного наблюдения к моменту следующего наблюдения будем называть шагом.

Если значения членов временного ряда точно определены какой-либо математической функцией, то временной ряд называется детерминированным. Если эти значения могут быть описаны только с помощью распределения вероятностей, временной ряд называется случайным.

Явление, развивающееся во времени согласно законам теории вероятностей, называется стохастическим процессом. В дальнейшем будем называть его просто процессом.

Анализируемый отрезок временного ряда может рассматриваться как одна частная реализация (выборка) изучаемого стохастического процесса, генерируемого скрытым вероятностным механизмом.

Среди стохастических процессов выделяют класс процессов, называемых стационарными. Обозначим член временного ряда, наблюденный в момент t, через x_t. Стохастический процесс называется стационарным, если его свойства не изменяются во времени. В частности, он имеет постоянное математическое ожидание 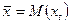(т. е. среднее значение, относительно которого он варьирует), постоянную дисперсию 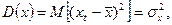определяющую размах его колебаний относительно среднего значения, а также постоянную автоковариацию и коэффициенты автокорреляции. Ковариация между значениями x_t и x_t+k отделенными интервалом в k единиц времени, называется автоковариацией с лагом (задержкой) k и определяется как

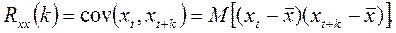
Для стационарных процессов автоковариация зависит только от лага k и 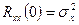. Автокорреляция с лагом k является лишь нормированной автоковариацией и равна:

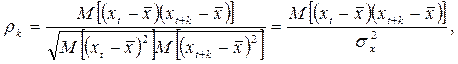
так как для стационарного процесса 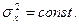. Таким образом, k-й коэффициент автокорреляции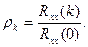

Он обладает тем свойством, что .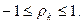

Для описания временных рядов используются математические модели. Представим, что временной ряд x_t, генерируемый некоторой моделью, можно представить в виде двух компонент

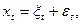
где величина ε_t генерируется случайным неавтокоррелированным процессом с нулевым математическим ожиданием и конечной (не обязательно постоянной) дисперсией, а величина ξ_t может быть генерирована либо детерминированной функцией, либо случайным процессом, либо какой-нибудь их комбинацией. Величины ε_t и ξ_t различаются характером воздействия на значения последующих членов ряда. Переменная ε_t влияет только на значение синхронного ей члена ряда, в то время как величина ξ_t в известной степени определяет значение нескольких или всех последующих членов ряда. Через величину ξ_t осуществляется взаимодействие членов ряда. Таким образом, в ней содержится информация, необходимая для получения прогнозов.

Назовем величину ξ_t уровнем ряда в момент t, а закон эволюции уровня во времени — трендом. Таким образом, тренд может быть выражен как детерминированной, так и случайной функциями, либо их комбинацией. Стохастические тренды имеют, например, ряды со случайным уровнем или случайным скачкообразным характером роста.

Приведем пример детерминированного тренда:

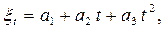
где а₁, а₂, а₃ — постоянные коэффициенты;

t — время.

Пример случайного тренда:

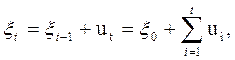
где ξ_о — некоторое начальное значение;

u_t — случайная переменная.

Пример тренда смешанного типа:

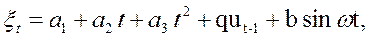
где a₁, a₂, q, b, ω — постоянные коэффициенты;

u_t — случайная переменная.

Известно множество определений уровня и тренда ряда. Существующие понятия тренда противоречивы и имеют условный характер. Каждое из этих определений скорее указывает на частный способ оценки тренда у, а не на его сущность. Очень часто под трендом понимают детерминированную составляющую процесса, что значительно обедняет содержание термина и препятствует его применению для анализа временных рядов в общем случае.

Компоненты временного ряда ξ_t и ε_t ненаблюдаемы. Они являются теоретическими величинами. Их выделение и составляет предмет анализа временного ряда в задаче прогнозирования. Оценку будущих членов ряда обычно делают по прогнозной модели. Прогнозная модель - это модель, аппроксимирующая тренд. Прогнозы — это оценки будущих уровней ряда, а последовательность прогнозов для различных периодов упреждения τ = 1, 2, ..., k составляет оценку тренда.

При построении прогнозной модели выдвигается гипотеза о динамике величины ξ_t , т. е. о характере тренда.

Однако в связи с тем, что уверенность в гипотезе всегда относительна, рассматриваемые модели наделяются адаптивными свойствами, способностью к корректировке исходной гипотезы или даже к замене ее другой, более адекватно (с точки зрения точности прогнозов) отражающей поведение реального ряда.

Простейшая адаптивная модель основывается на вычислении так называемой экспоненциальной средней.