Уравнения кинетостатики

Слово «кинетостатика» образовано сочетанием двух греческих слов: kinetos – движение, statos – покой, равновесие. То есть, «кинетостатика» означает «равновесие в движении» или «динамическое равновесие». Уравнения кинетостатики звена механизма, как твердого тела, в векторной форме имеют вид:

, ,

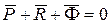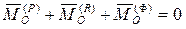Здесь 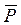, 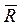- главные векторы активных сил и сил реакций, приложенных к звену, 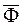- главный вектор сил инерции звена; 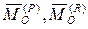- главные моменты активных сил и сил реакций относительно некоторого центра O, 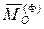- главный вектор сил инерции звена относительно того же центра O. Главный вектор и главный момент сил инерции звена вычисляются по формулам:

, ,

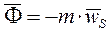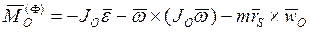где 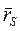- радиус-вектор, 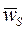- ускорение центра масс, 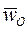- ускорение центра O, m – масса звена; 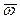- угловая скорость, 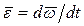- угловое ускорение звена, J_O – тензор инерции звена относительно центра O. Таким образом, в каждый момент времени, действующие на звено силы уравновешиваются силами инерции звена, а моменты сил, приложенные к звену, уравновешиваются моментами сил инерции звена. Это утверждение представляет собой известный из теоретической механики принцип Даламбера, сформулированный по отношению к твердому телу.

В случае плоского механизма, вектор главного момента сил инерции звена относительно центра масс S будет определяться своими декартовыми координатами:

, , .

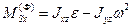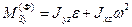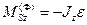В проекциях на оси декартовой системы координат векторные уравнения кинетостатики звена равносильны шести скалярным уравнениям:

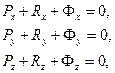
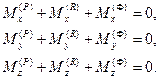
Если механизм плоский и Oxy – плоскость движения звеньев, то три из приведенной системы уравнений становятся тождественно равными нулю и остаются лишь три скалярных уравнения кинетостатики для каждого звена:

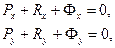
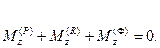
Таким образом, для пространственного механизма требуется составить и решить 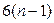, а для плоского - 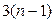скалярных уравнений кинетостатики, где n – число звеньев механизма. Эти системы уравнений могут быть решены аналитически, а в случае плоского механизма векторные уравнения сил удобно решать с помощью метода векторных планов. Для каждого нового положения механизма систему уравнений кинетостатики необходимо составлять и решать заново. Поэтому силовой расчет механизма является довольно трудоемкой задачей, решение которой целесообразно автоматизировать с помощью компьютера.

Теорема Жуковского

Как известно, динамика одноподвижного механизма с идеальными связями подчиняется принципу Даламбера, который может быть сформулирован в следующем виде:

,

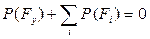где 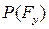- мгновенная мощность уравновешивающей силы, 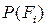- мгновенные мощности активных сил, действующих на механизм, включая силы инерции. В качестве уравновешивающей силы выступает сила, развиваемая приводом механизма.

В случаях, когда ставится задача вычисления только обобщенных движущих сил, проводить трудоемкий расчет по уравнениям кинетостатики нецелесообразно. Если имеются векторные планы скоростей, то определить движущую силу или момент можно методом Жуковского, который основан на принципе Даламбера и теореме Жуковского:

· Мгновенная мощность силы, приложенной к звену, пропорциональна моменту этой же силы относительно полюса повернутого на 90⁰ плана скоростей механизма.

Для доказательства теоремы рассмотрим звено механизма (Рис. 28,а).

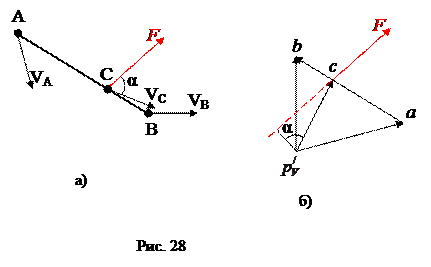Мгновенная мощность силы F определяется равенством:

,

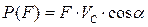где V_C – абсолютная скорость точки С, в которой действует сила.

Момент силы F относительно полюса повернутого на 90⁰ плана скоростей, как видно из рис. 28б, вычисляется по формуле:

.

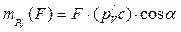Так как 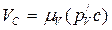, где 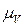- масштаб плана скоростей, то окончательно имеем:

,

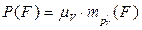что и требовалось доказать.