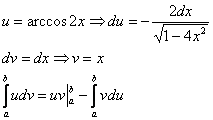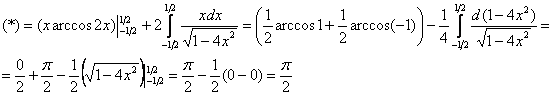Находим новые переделы интегрирования
Это достаточно просто. Смотрим на нашу замену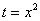 
и старые пределы интегрирования 
; 
.
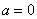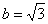Сначала подставляем в выражение замены t=x2 нижний предел интегрирования, то есть, ноль:
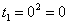
Потом подставляем в выражение замены t=x2 верхний предел интегрирования, то есть, корень из трёх:
.
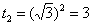Продолжаем решение.
(1) В соответствии с выбранной заменой переменных записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице. Константу (1/2) лучше оставить за скобками (можно этого и не делать), чтобы она не мешалась в дальнейших вычислениях.
Справа отчеркиваем линию с указанием новых пределов интегрирования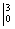 
– это подготовка для применения формулы Ньютона-Лейбница.
(3) Используем формулу Ньютона-Лейбница.
Ответ стремимся записать в максимально компактном виде, здесь использованы свойства логарифмов.
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену и подставили числа, никаких обратных замен проводить не надо.
А сейчас пара примеров для самостоятельного решения.
Какие замены проводить – постарайтесь догадаться самостоятельно.
Пример 6
Вычислить определенный интеграл
.
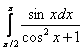Пример 7
Вычислить определенный интеграл
.
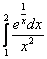Это примеры для самостоятельного решения. Решения и ответы в конце урока.
Метод интегрирования по частям в определенном интеграле
Здесь новизны еще меньше. Все выкладки статьи Интегрирование по частям в неопределенном интеграле в полной мере справедливы и для определенного интеграла. Плюс только одна деталь: в формуле интегрирования по частям добавляются пределы интегрирования и она принимает вид:
.
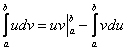Формулу Ньютона-Лейбница здесь необходимо применить дважды: для вычисления произведения uv и, после того, как мы возьмем интеграл
.
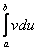Тип интеграла для примера опять подбираем такой, который еще нигде не встречался в курсе. Пример не самый простой, но очень и очень познавательный.
Пример 8
Вычислить определенный интеграл
.
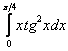Решаем.
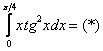
Интегрируем по частям:
У кого возникли трудности с интегралом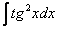 
, загляните на урок Интегралы от тригонометрических функций, там он подробно разобран.
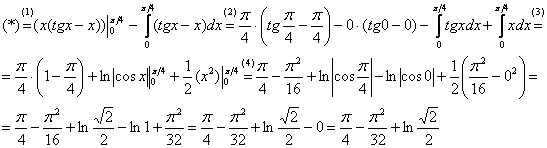
(1) Записываем решение в соответствии с формулой интегрирования по частям.
(2) Для произведения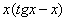 
применяем формулу Ньютона-Лейбница. Для оставшегося интеграла используем свойства линейности, разделяя его на два интеграла.
(3) Берем два оставшихся интеграла.Не путаемся в знаках! Интеграл от тангенса также был разобран на уроке Интегралы от тригонометрических функций.
(4) Применяем формулу Ньютона-Лейбница для двух найденных первообразных.
Уважаемый студент, распечатай и сохрани:
Что делать, если дан определенный интеграл, который кажется сложным или не сразу понятно, как его решать?
1) Сначала находим неопределенный интеграл (первообразную функцию). Если на первом же этапе ничего не вышло, дальше переходить к Ньютону и Лейбницем бессмысленно. Путь только один – повышать свой уровень знаний и навыков в решении неопределенных интегралов.
2) Проверяем найденную первообразную функцию дифференцированием. Если она найдена неверно, третий шаг будет напрасной тратой времени.
3) Используем формулу Ньютона-Лейбница. Все вычисления проводим ПРЕДЕЛЬНО ВНИМАТЕЛЬНО – тут самое слабое звено задания.
Интеграл для самостоятельного решения.
Пример 9
Вычислить определенный интеграл
.
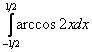Решение и ответ где-то рядом.
Решения и ответы:
Пример 2: Решение:
.
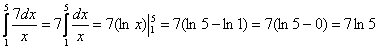Пример 4: Решение:
.
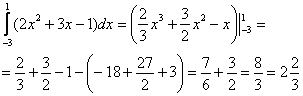Пример 6: Решение:
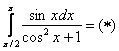
Проведем замену переменной: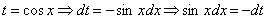 
,
Новые переделы интегрирования:
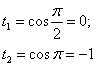
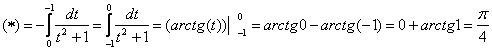
Примечания: В рассмотренном интеграле – как раз тот случай, когда уместно применить свойство определенного интеграла
.
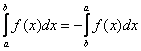Пример 7: Решение:
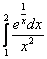
Замена: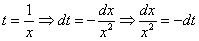 
.
Новые пределы интегрирования:
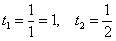
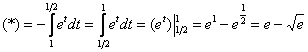
Пример 9: Решение:
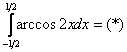
Интегрируем по частям:
