Суть метода искусственного базиса

В случаях, когда сразу не выделяются базисные переменные (а они сразу выделяются только после приведения к каноническому виду задачи, в которой имеются только неравенства типа «≤» при неотрицательных правых частях) можно применять так называемый метод искусственного базиса, который является по сути разновидностью симплекс-метода.

Пусть задача приведена к каноническому виду (1.6), в котором в некоторых уравнениях, скажем в i₁-м, i₂-м, …, i_s-м, явно не выделяются базисные переменные. Добавим в эти уравнения искусственные переменныеx_m+1, x_m+2, …, x_m+s, а в целевую функцию - слагаемые ±Mx_m+1, ±Mx_m+2, …, ±Mx_m+s, где M>>1 (M - достаточно большое положительное число) причём «±» - это «+», если решается задача на min, и «±» - это «-», если решается задача на max. Получается новая задача, которая называется дополнительной или вспомогательной.

Например, вспомогательная (дополнительная) задача с искусственными переменными для задачи (1.5) будет иметь вид

c₁x₁+c₂x₂+…+c_nx_n+Mx_n+m+1+Mx_n+m+2+…+Mx_n+2m®min

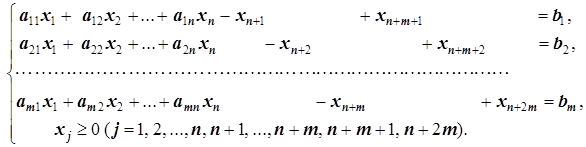
Аналогично, если задача (2.1) решается на max и придётся вводить искусственные переменные во все ограничения, то получаем следующую вспомогательную задачу:

c₁x₁+c₂x₂+…+c_nx_n-Mx_n+1-Mx_{n +2}-…-Mx_n+m®max

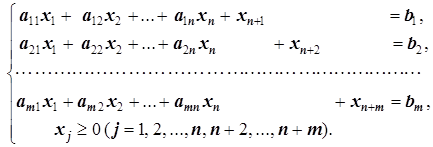(5.1)

5.1.1. Если ( 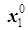, , 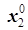…, , , 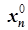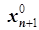…, 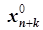) оптимальное решение вспомогательной задачи, где 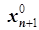, …, 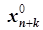- значения искусственных переменных, 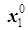, , 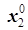…, 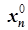- значения переменных в исходной задаче в канонической форме, то 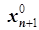=…= =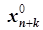0 и ( 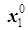, , 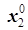…, 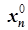) - оптимальное решение исходной задачи. При этом значения целевой функции исходной и вспомогательной задач совпадают.

Отсюда получаем, что для решения задачи линейного программирования, методом искусственного базиса достаточно:

1. Привести задачу к каноническому виду.

2. Если в задаче в каноническом виде нет базиса из единичных векторов, то составить вспомогательную задачу (если в задаче в каноническом виде имеется базис из единичных векторов, то задача решается обычным симплекс-методом).

3. Решить вспомогательную задачу, и если ( 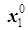, , 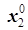…, , , 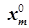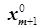…, 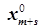) - оптимальное решение вспомогательной задачи, где x₁, x₂, …, x_m - основные и дополнительные переменные (из задачи в каноническом виде), x_m+1, x_m+2, …, x_m+s - искусственные переменные то ( 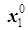, , 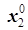…, 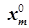) - решение задачи в каноническом виде. Оптимальное значение целевой функции вспомогательной задачи равно оптимальному значению исходной задачи.

При этом к вспомогательной задаче применяется обычный симплекс-метод с некоторыми своими особенностями:

1. Так как целевая функция вспомогательной задачи имеет слагаемые с коэффициентами ±M, то оценки D_k имеют вид 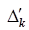± 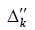M, причём M - достаточно большое число. Поэтому при 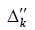≠0 знак D_k фактически определяется знаком при 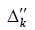. В связи с этим в симплекс-таблице на начальном этапе (пока в базис входят искусственные переменные) вместо одной строки D_k записывают две строк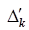и и 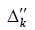, и при применении критерия оптимальности ориентируются только на строку .

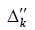2. Искусственные переменные по мере их выведения из базиса исключаются из дальнейшего рассмотрения.

3. После того, как все искусственные переменные будут выведены из базиса, коэффициенты D_k при M будут равны нулю, в таблице остаётся только строка 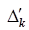=D_k.

Пример. Решить пример из предыдущего параграфа методом искусственного базиса.

Решение. Напоминаем задачу:

-3x₁+x₂+2x₃ ® max(min)

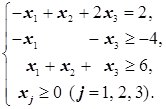
1. Приведём задачу к каноническому виду:

-3x₁+x₂+2x₃ ® max(min)

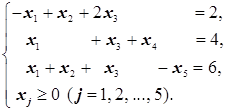
2. В базис в виде единичного вектора входит только вектор при x₄, то есть переменная во втором уравнении. В первое и третье уравнения системы ограничений вводим искусственные переменные x₆ и x₇:

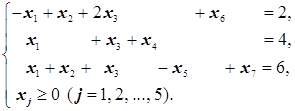
В целевую функцию они войдут с коэффициентами M или -M в зависимости от того, решается задача на min или на max.

Решим задачу на максимум. Тогда вспомогательная задача - следующая:

-3x₁+x₂+2x₃-Mx₆-Mx₇ ® max

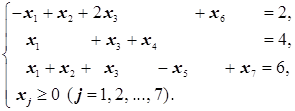
3. Решаем полученную вспомогательную задачу с применением симплекс-таблиц:

Базис

Сб

Своб. чл.

-3

-M

-M

q2

q3

x1

x2

x3

x4

x5

x6

x7

x6

-M

-1

min

x4

-

x7

-M

-1

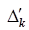-1

-2

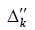-8

-2

-3

Здесь D₂=-2M-1, D₃=-3M-2. Коэффициенты при M записаны в строке 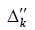. Имеем, что D₂<0 и D₃<0, то есть для переменных x₂ и x₃ нарушается критерий оптимальности. Поэтому в базис будем вводить x₂ или x₃. Какую именно из этих переменных, и вместо какой из искусственных (вместо x₆ или вместо x₇), определяем с помощью столбцов q₂ и q₃. На пересечении столбца q₂ и строк 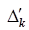и 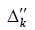числа соответственно 2 и 4 означают, что в случае включения в базис x₂ значение функции возрастёт на -q₂D₂=4M+2, а в случае включения в базис x₃ значение функции возрастёт на -q₃D₃=3M+2<-q₂D₂. Поэтому в базис включаем x₂ (что обеспечивает большее возрастание функции и в конечном итоге ускоряет процесс решения задачи). Так как min 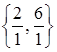=2 достигается в строке x₆, то из базиса исключаем x₆. Строим новую симплекс-таблицу, в который уже столбец с искусственной переменной x₆ отсутствует (вычеркнут), так как искусственная переменная x₆ из дальнейшего процесса исключается. В новой таблице коэффициент при x₂ в первой строке (которая теперь соответствует новой базисной переменной x₂) равен 1, а во второй равен нулю. Поэтому первые две строки в новую таблицу переписываем из старой. Для того, чтобы в строке x₇ при x₂ получить 0, из строки x₇ в старой таблице вычитаем новую первую. Получаем следующую, очередную, таблицу:

Базис

Сб

Своб. чл.

-3

-M

-M

q1

x1

x2

x3

x4

x5

x6

x7

x2

-1

-

x4

x7

-M

-1

-1

min

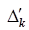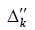-4

-2

Так как D_k<0 только для одного значения k=1, а именно, D₁=-2M+2<0 (напоминаем, что M - достаточно большое число, так что -2M<2 и D₁<0), то ищем только отношения q₁. Минимум этих отношений достигается в строке x₇: min 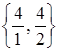=2. Поэтому искусственная переменная исключается из базиса, а вместо неё в базис включается x₁.

Искусственные переменные теперь исключены из базиса. Поэтому дальше работаем с обычной симплекс-таблицей, в которой новая третья строка (соответствующая переменной x₁) получается делением старой третьей строки на 2. Затем эту новую третью прибавляем к старой первой и вычитаем из старой второй. В результате в новой таблице в столбце x₁ появятся соответственно 0, 0 и 1:

Базис	Сб	Своб. чл.	-3
x1	x2	x3	x4	x5
x2					3/2		-1/2
x4					3/2		1/2
x7	-3				-1/2		-1/2
Dk	-2

В полученной таблице D_k³0 для всех k=1, 2, …, 5, то есть критерий оптимальности выполнен. Поэтому X₀=(2; 4; 0) является оптимальным решением, при котором значение целевой функции равно -2 (x₄ в окончательном ответе не учитывается, так как она является дополнительной переменной, и не входит в первоначальную задачу).

Решим задачу на минимум (min). Тогда вспомогательная задача - следующая:

-3x₁+x₂+2x₃-Mx₆-Mx₇ ® max

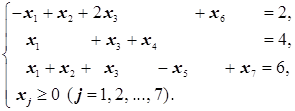
Как и выше, решаем полученную вспомогательную задачу с применением симплекс-таблицы:

Базис

Сб

Своб. чл.

-3

M

M

q2

q3

x1

x2

x3

x4

x5

x6

x7

x6

M

-1

min

x4

-

x7

M

-1

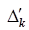-1

-2

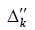-1

Критерий оптимальности нарушается для переменных x₂ и x₃: D₂=2M-1>0, D₃=3M-2>0. Так как -q₂D₂=-4M+2 по абсолютной величине превосходит -q₃D₃=-3M+2, то в базис включаем x₂. При этом min 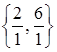=2 достигается в строке x₆, и из базиса исключаем x₆. Переход к новой таблице аналогичен переходу при решении задачи на max:

Базис

Сб

Своб. чл.

-3

-M

-M

q1

x1

x2

x3

x4

x5

x6

x7

x2

-1

-

x4

x7

-M

-1

-1

min

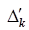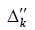-1

-1

Теперь D₁>0. Поэтому переход к новой таблице аналогичен соответствующему переходу при решении задачи на max: в базис вводится x₁ вместо x₇:

Базис	Сб	Своб. чл.	-3					q3	q5
x1	x2	x3	x4	x5
x2					3/2		-1/2	8/3	-
x4					3/2		1/2	4/3
x7	-3				-1/2		-1/2	-	-
Dk	-2						-4/3	-4

Имеем D₃=1>0 и D₅=1>0. Так как |-q₅D₅|=|-q₃D₃|, то вводим в базис x₅ (вместо x₄): сначала умножаем 2-ю строку на 2, а затем новую вторую строку, умноженную на ½, прибавляем к первой и третьей (фактически вторую старую прибавляем к первой и третьей):

Базис	Сб	Своб. чл.	-3
x1	x2	x3	x4	x5
x2
x4
x7	-3
Dk	-6			-2	-2

В полученной таблице D_k£0 для всех k=1, 2, …, 5, то есть критерий оптимальности выполнен. Поэтому X₀=(4; 6; 0) является оптимальным решением, при котором значение целевой функции равно -6.

Ответ: F_min=-6, минимум достигается в точке X₂=(4; 6; 0);

F_max=-2, максимум достигается в точке X₁=(2; 4; 0).

5.2. Упражнение. Решить соответствующие задачи линейного программирования из Упражнения 1.3 методом искусственного базиса.

Теория двойственности