Острый угол между прямой и плоскостью

Ax + By + Сz + D = О определяется по формуле

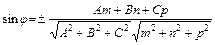
Условие параллельности прямой и плоскости имеет вид

Am + Bn + Ср = 0.

Условие перпендикулярности прямой и плоскости имеет вид

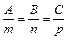
Уравнение пучка плоскостей, проходящих через данную прямую 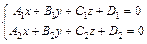имеет вид:

Ax +By + Cz + D + λ(A₁ x +B₁ y + C₁ z+ D₁) =0

Пример. Найти уравнение плоскости, проходящей через точку Р(1, 2, —1) перпендикулярно прямой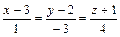

Решение:

Уравнение плоскости, проходящей через точку Р(1, 2, -1), напишем на основании уравнения А(х-х₁)+В(у-у₁)+С(z-z₁)=0 в виде А(х-1)+В(у-2)+С(z+1)=0

Пользуясь условием 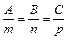перпендикулярности прямой и плоскости, заменив в последнем уравнении величины А, В и С им пропорциональными величинами т, п и р из уравнений пря­мой, т. е. числами 1, -3 и 4, и получим

1(х-1)-3(у-2)+4(z+1)= 0. а после упрощений получим x - 3у+4z+9=0.

Кривые второго порядка.

1. Окружность. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки. Уравнение окружности имеет вид

(х - а)² + (y - b)² = r²

где a и b—координаты центра окружности, a r—радиус ок­ружности.

Если же центр окружности находится в начале координат, то ее уравнение имеет вид

x² + y² = r²

2. Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух данных фиксированных точек (фокусов) есть для всех точек эллипса одна и та же по­стоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

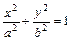
где а — большая полуось эллипса,b — малая полуось эллипса.

Если 2с — расстояние между фокусами, то между а, b и с (если а > b) существует соотношение

а² - b² = с².

Эксцентриситетом эллипса называется отношение, расстояния между фокусами этого эллипса к длине его большой оси

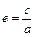
У эллипса эксцентриситет е < 1 (так как с < о), а его фокусы лежат на большой оси.

3. Гипербола. Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных фиксированных точек (фокусов) гиперболы есть одна и та же постоянная вели­чина.Предполагается, что эта постоянная величинанеравна нулю и меньше,чем расстояние между фокусами.

Простейшее уравнение гиперболы

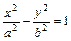
Здесь а - действительная полуось гиперболы, b—мнимая полуось гиперболы.

Если 2с — расстояние между фокусами гиперболы, то между а, b и с существует соотношение

a² + b² = с²

При b= а гипербола называется равносторонней. Уравнение равносторонней гиперболы имеет вид

x² - y² = a²

фокусы гиперболы лежат на ее действительной оси. Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к длине ее действительной оси

е= 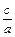.