Основные этапы экстремального эксперимента.

При постановке экстремальных экспериментов на первом этапе находят область оптимума. На втором этапе стремятся получить более полное представление о поверхности отклика в области оптимума. Решение экстремальной задачи предусматривает получение функции отклика и нахождение с помощью ее оптимальных условий протекания процесса.

Часто приходится решать экстремальные задачи при неполном знании механизма процесса. В этом случае зависимость функции отклика неизвестна, и поэтому вынуждены ограничиваться представлением ее полиномом вида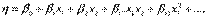

где b₀,b₁,…-коэф регрессии при соответствующих переменных.

По результатам эксперимента можно определить только выборочные коэф регрессии b₀, b₁, b₂, b₁₂, …, которые являются лишь оценками теоретических коэффициентов регрессииb₀, b₁, b₂, b₁₂,… . Уравнение регрессии:

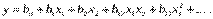
На первом этапе планирования эксперимента функцию отклика выражают полиномом первой степени:

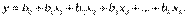(1)

Для определения коэффициентов уравнения (1) достаточно реализовать факторный эксперимент типа 2^k, где k- число факторов. Планы экспериментов типа 2^k называют планами первого порядка.

Область оптимума чаще всего удается описать полиномом второй степени:

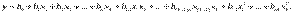
Чтобы определить все коэффициенты уравнения (2), необходимо реализовать план эксперимента типа 3^k. Планы эксперимента типа 3^k называют планами второго порядка.

21. Корреляционный анализ – статистический метод изучения взаимосвязи между двумя и более случайными величинами. В качестве случайных величин в эмпирических исследованиях выступают значения переменных, измеряемые свойства исследуемых объектов наблюдения. Суть корреляционного анализа заключается в расчете коэффициентов корреляции. Коэффициенты корреляции могут принимать, как правило, положительные и отрицательные значения. Знак коэффициента корреляции позволяет интерпретировать направление связи, а абсолютное значение – силу связи.

Способ расчета коэффициентов корреляции зависит от шкал измерения переменных, между которыми исследуется взаимосвязь. Для переменных, измеряемых в количественной шкале (интервальной шкале или шкале отношений), рассчитывают ковариацию или корреляционный момент, а на его основе линейный коэффициент корреляции (коэффициент корреляции Пирсона).

Корреляционный анализ не позволяет определить форму связи между переменными и предсказывать значения одной зависимой переменной по одной или нескольким независимым. Для этого, например, для количественных переменных применяется линейный регрессионный анализ.

22. Регрессионный анализ - метод моделирования измеряемых данных и исследования их свойств. Данные состоят из пар значений зависимой переменной (переменной отклика) и независимой переменной (объясняющей переменной). Регрессионная модель есть функция независимой переменной и параметров с добавленной случайной переменной.

Корреляционный анализ и регрессионный анализ являются смежными разделами математической статистики, и предназначаются для изучения по выборочным данным статистической зависимости ряда величин; некоторые из которых являются случайными. При статистической зависимости величины не связаны функционально, но как случайные величины заданы совместным распределением вероятностей.

Исследование зависимости случайных величин приводит к моделям регрессии и регрессионному анализу на базе выборочных данных.

Числовые данные обычно имеют между собой явные (известные) или неявные (скрытые) связи.

Явно связаны показатели, которые получены методами прямого счета, т. е. вычислены по заранее известным формулам. Связи же второго типа (неявные) заранее неизвестны.