Условия однозначности для процессов теплопроводности
Дифференциальное уравнение теплопроводности описывает явление в самом общем виде, т.е описывает класс явлений теплопроводности. Чтобы рассмотреть конкретный процесс следует дать его полное математическое описание. Математическая постановка задачи включает в себя дифференциальное уравнение теплопроводности и условия однозначности. Частные особенности конкретного процесса теплопроводности называются условиями однозначности или краевыми условиями, которые включают в себя:
Геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;
Физические условия, характеризующие физические свойства тела и окружающей среды;
Временные (начальные) условия, характеризующие распределение температур в теле в начальный момент времени;
Граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.
Граничные условия могут быть заданы несколькими способами.
Граничные условия первого рода. Задается распределение температуры на поверхности тела для каждого момента времени
tпов=f(х,у,z, 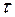 ).
).
В частном случае, когда температура на поверхности является постоянной (для стационарной теплопроводности), то tпов=const. Это условие обычно называют условием Дирихле.
К граничным условиям І рода можно отнести задачи разогрева системы при заданном изменении температуры на границе или при весьма интенсивном теплообмене.
Граничные условия второго рода. Задается значение плотности теплового потока для каждой точки поверхности и любого момента времени
qпов= f(х,у,z, 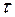 ).
).
В простейшем случае, для стационарной теплопроводности, когда плотность теплового потока по поверхности и во времени остается постоянной qпов=const. Эти условия обычно называют условием Неймана.
Такой случай имеет место при нагревании изделий в высокотемпературных печах.
Граничные условия третьего рода. При этом задаются температура окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. Процесс охлаждения или нагревания тел описывается законом Ньютона-Рихмана
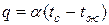 ,
,
где 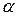 - коэффициент теплоотдачи, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой. Коэффициент теплоотдачи зависит от большого числа факторов. Однако во многих случаях при решении задач теплопроводности его можно считать неизменным.
- коэффициент теплоотдачи, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой. Коэффициент теплоотдачи зависит от большого числа факторов. Однако во многих случаях при решении задач теплопроводности его можно считать неизменным.
Плотность потока, подводимая за счет теплопроводности к поверхности тела, определяется по закону Фурье. Следовательно, на основании закона сохранения энергии
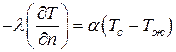 .
.
Граничные условия четвертого рода (сопряжения). Задаются как условия равенства температуры и плотностей теплового потока на поверхности соприкосновения двух сред или тел
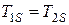 ,
,
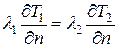 .
.
Эти условия называют условиями идеального теплового контакта. Задачи с такими условиями ставятся при расчетах многослойных теплоизоляционных покрытий в металлургической, авиационной и космической технике.
Вопросы к введению и теме 1.
1. Дайте определения основных видов теплообмена.
2. Что называется температурным полем? Дать определение стационарного и нестационарного температурного поля.
3. Что называют изотермической поверхностью и температурным градиентом?
4. Сформулируйте гипотезу Фурье, объясните знак «минус» в уравнении.
5. Что называют тепловым потоком?
6. Что такое коэффициент теплопроводности, его размерность. Поясните физический смысл.
7. От каких факторов зависит коэффициент теплопроводности? В каких пределах изменяется его значение для газов, жидких сред и твердых материалов?
8. Вывести дифференциальное уравнение теплопроводности. Проанализировать его.
9. Записать дифференциальное уравнение теплопроводности для стационарного и нестационарного процессов.
10. Что такое коэффициент температуропроводности, его размерность, что он характеризует?
11. Что значит сформулировать математическую постановку задачи?
12. Что включают в себя условия однозначности?
13. Как задаются граничные условия первого, второго и третьего родов?
14. Записать уравнение Ньютона-Рихмана. Дать определение коэффициента теплоотдачи, его размерность.
