Проективная плоскость и ее модели
БИЛЕТ №16
Проективное пространство – некоторое непустое множество Р элементов, называемых точками, в предположении, что задано отображение f: 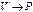 , которое удовлетворяет аксиомам проективного пространства:
, которое удовлетворяет аксиомам проективного пространства:
1) Отображение f сюръективно, т.е. любой элемент из Р имеет хотя бы один прообраз.
2) Равенство 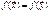 вып-ся тогда и только тогда, когда векторы
вып-ся тогда и только тогда, когда векторы 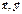 коллинеарны.
коллинеарны.
Здесь 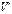 — множество ненулевых векторов некоторого векторного пространства V.
— множество ненулевых векторов некоторого векторного пространства V.
Если найдено конкретное множество Р и конкретное отображение f, то говорят, что построена интерпретация (реализация) данной системы аксиом. Само множество Р называется моделью проективного пространства. Рассмотрим некоторые модели проективной плоскости.
 1. Пусть А3 — трехмерное аффинное пространство над векторным пространством V. Обозначим через Р2 множество всех прямых пространства А3, проходящих через некоторую фиксированную точку О (связка прямых с центром в точке О). Рассмотрим отображение
1. Пусть А3 — трехмерное аффинное пространство над векторным пространством V. Обозначим через Р2 множество всех прямых пространства А3, проходящих через некоторую фиксированную точку О (связка прямых с центром в точке О). Рассмотрим отображение 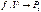 по следующему закону: ненулевому вектору
по следующему закону: ненулевому вектору 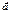 из V поставим в соответствие прямую, проходящую через точку О и параллельную вектору
из V поставим в соответствие прямую, проходящую через точку О и параллельную вектору 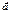 . Отображение f удовлетворяет аксиомам проективного пространства, поэтому Р2 — модель проективной плоскости. В этой модели., проективными точками являются прямые связки с центром О, а проективными прямыми — множество всех прямых, проходящих через точку О и лежащих в некоторой плоскости.
. Отображение f удовлетворяет аксиомам проективного пространства, поэтому Р2 — модель проективной плоскости. В этой модели., проективными точками являются прямые связки с центром О, а проективными прямыми — множество всех прямых, проходящих через точку О и лежащих в некоторой плоскости.
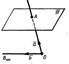
2. Построим другую модель проективной плоскости, основанную на понятии расширенного евклидова пространства. Пусть 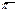 — расширенная плоскость трехмерного расширенного евклидова пр-ва над векторным пр-вом V. Возьмем собственную точку О этого пространства, не лежащую в плоскости
— расширенная плоскость трехмерного расширенного евклидова пр-ва над векторным пр-вом V. Возьмем собственную точку О этого пространства, не лежащую в плоскости 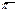 , и рассмотрим отображение
, и рассмотрим отображение 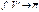 по следующему закону: каждому ненулевому вектору
по следующему закону: каждому ненулевому вектору 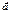 из V поставим в соответствие точку, в которой прямая, проходящая через О параллельно вектору а, пересекает плоскость
из V поставим в соответствие точку, в которой прямая, проходящая через О параллельно вектору а, пересекает плоскость 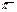 (рис.). Так как любая прямая, проходящая через точку О, пересекает плоскость
(рис.). Так как любая прямая, проходящая через точку О, пересекает плоскость 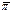 в собственной или несобственной точке, то каждому ненулевому вектору ставится в соответствие некоторая (собственная или несобственная) точка плоскости
в собственной или несобственной точке, то каждому ненулевому вектору ставится в соответствие некоторая (собственная или несобственная) точка плоскости 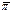 . На рис. вектору
. На рис. вектору 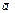 соответствует собственная точка А, а вектору
соответствует собственная точка А, а вектору 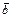 — несобственная точка
— несобственная точка 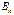 .
.
Примем теперь новое соглашение: собственные и несобственные точки плоскости 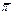 будем считать равноправными; их будем называть просто проективными точками. Если через Р2 обозначить множество всех проективных точек, то f есть отображение множества векторов
будем считать равноправными; их будем называть просто проективными точками. Если через Р2 обозначить множество всех проективных точек, то f есть отображение множества векторов 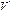 на множество Р2. Это отображение удовлетворяет аксиомам проективного пространства, поэтому P2 — модель проективной плоскости. В этой модели точками являются проективные точки, т. е. собственные и несобственные точки расширенной плоскости
на множество Р2. Это отображение удовлетворяет аксиомам проективного пространства, поэтому P2 — модель проективной плоскости. В этой модели точками являются проективные точки, т. е. собственные и несобственные точки расширенной плоскости 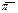 , а прямыми — проективные прямые, т. е. обычные (собственные) прямые плоскости
, а прямыми — проективные прямые, т. е. обычные (собственные) прямые плоскости 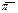 , каждая из которых пополнена несобственной точкой, и несобственная прямая плоскости
, каждая из которых пополнена несобственной точкой, и несобственная прямая плоскости 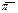 .
.
Деление с остатком
Ограничимся рассмотрением многочленов с одним аргументом над данным числовым полем.
Теорема. Каковы бы ни были два многочлена (над данным полем)
f(x)=anxn+ an–1 xn–1+…+ a1 x+a0
и φ(x)= bmxm+ bm–1 xm–1+…+ b1 x+b0
причем φ(x)≠0, существует (над тем же полем) единственная пара многочленов q(x) и r(х), удовлетворяющих следующим условиям:
1°. степень r(х) меньше m или r(x)=0,
2°. имеет место тождество:
f(x)≡q(x)φ(x) + r(x). (1)
Многочлены q(x) и r(x) называются соответственно неполным частным и остатком.
Нахождение многочленов q(x) и r(х) называется делением с остатком многочлена f(x) на многочлен φ(x).
Доказательство. Если т>п, то тождество (1) удовлетворяется при q(x)≡0 и r(x) ≡f(x). Пусть п ≥ m; разделим старший член апхп многочлена f(x) на старший член bтхт многочлена φ(x), умножим полученное частное на φ(x) и вычтем произведение из f(x): 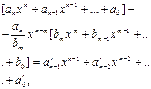 (2)
(2)
где 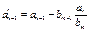 и т.д., откуда: f(x)=(αn/bm)xn–mφ(x)+R1(x)
и т.д., откуда: f(x)=(αn/bm)xn–mφ(x)+R1(x)
где R1(x) многочлен, находящийся в правой части тождества (2). Этот многочлен называется первым остатком отделения f(х) на φ(x). Пусть п1 степень первого остатка и а'п1 его старший коэффициент (если а’п–1 ≠0, то п1 = п—1).
Если п1 ≥m, то, поступив с R1(x) так же, как с f(x), получим:
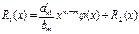 и
и 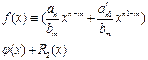
Многочлен R2(х) называется вторым остатком от деления f(x) на φ(х) и т. д. Для получения последующего остатка надо старший член предыдущего остатка разделить на старший член многочлена φ(x), умножить на полученное частное многочлен ф('я) и вычесть произведение из предыдущего остатка. Описанный процесс можно продолжать, пока не получится в остатке многочлен Rk(x) степени более низкой, чем m, либо Rk≡0. В результате этого процесса получится тождество (1), где 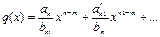 и
и  r(x)=Rk(x)Согласно изложенному, деление с остатком заключается в переходе от делимого к первому остатку, от первого остатка ко второму и т. д. при помощи единообразного выполнения одних и тех же операций. Обычно эти операции выполняются при помощи известной схемы (деление «углом»), __________________________
r(x)=Rk(x)Согласно изложенному, деление с остатком заключается в переходе от делимого к первому остатку, от первого остатка ко второму и т. д. при помощи единообразного выполнения одних и тех же операций. Обычно эти операции выполняются при помощи известной схемы (деление «углом»), __________________________
