Тема 1.1.1 Понятие множества. Элементы множества. Виды множества. Способы заданий.(1ч.)

РАЗДЕЛ 1: ЭЛЕМЕНТЫ ЛОГИКИ.

Тема 1.1: МНОЖЕСТВА и ОПЕРАЦИИ НАД НИМИ (10ч.)

Литература:

1. Виленкин Н.Я Математика. Учеб. пособ.для студентов пед. Институтов по спец.№2121 – «Педагогика и мет. Нач. обуч.», - М., Просвещение, 1977, с.25 – 37
2. Стойлова Л.П. Математика: учеб. пособие для студ. сред пед. учеб. заведений , 1998 г.с.6-43
3. Стойлова Л.П. Основы нач.курса математики: учеб.пособие для уч. педучилищ по спец. №2001, 1988 с.61-97
4. Аматова Г.М., Аматов М.А.Математика. Упражнения и задачи.

Тема 1.1.1 Понятие множества. Элементы множества. Виды множества. Способы заданий.(1ч.)

Итак, что же такое «множество?»

В науке, как и в жизни часто приходится рассматривать совокупности некоторых объектов как единое целое: флот, бригада, класс, род животных, набор, коллекция и т.д. Для математического описания этих совокупностей и было введено слово «множество». Множество книг в библиотеке, множество отрезков…

Множества принято обозначать прописными буквами ла­тинского алфавита: А, В, С, .... Z.

Таким образом, слово «множество» может применяется к объектам любой природы, выражает идею объединения объектов. Объекты, собранные в множество, называют элементами множества.

Элементы множества принято обозначать строчными бук­вами латинского алфавита: а, Ъ, с, ..., z.

Равные элементы в множествах не повторяются (каждый элемент множества берется только один раз. Например, множество букв в слове «математика» 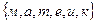записывается только один раз.

Способы задания множества:

1) Перечислением: А={ 5,8,3,6};

2) общим свойством (характеристически):

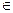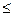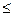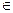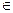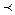Например: «быть двузначным числом» А={ х|х N и 10 х 99}, «множества А натуральных чисел» А={ х|х N }, «мн-во натуральных чисел меньших 7» обоз-ся А={ х|х N и х 7}.

Пример . Используя понятие характеристического свой­ства, зададим следующие множества:

А = {б, в, г, д, ж, з, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ};

В = {красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый};

С = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}.

Решение. Множества А, В, С заданы способом перечисления элементов. Используя характеристические свойства, указанные множества можно задать следующим образом:

А — множество согласных букв русского алфавита;

В — множество цветов радуги;

С — множество дней недели.

Пример Изобразим на числовой прямой элементы сле­дующих множеств:

а) А = {х\х ? N, 3 <х <10};

б) В = \х\х ? Z, -4 <х < 6};

в) С ={х\х ? R, -5 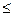х <8};

Решение, а) Элементами множества А являются натураль­ные числа от 3 до 10, т. е. А = {3, 4, 5, 6, 7, 8, 9, 10}. Можно изобразить эти числа точками на числовой прямой

б) Множество В состоит из всех целых чисел, находящихся в промежутке от —4 до 6, т. е. В = {—4, —3, —2, —1, 0, 1, 2, 3, 4, 5}.Число 6 не принадлежит множеству В, поскольку

х < 6. На чис­ловой прямой множество В изображается выколотой точкой.

в) Множество С состоит из всех действительных чисел, при­надлежащих промежутку от —5 до 8. Причем число —5 принад­лежит множеству С, а число 8 не принадлежит. Можно изобразить мно­жество С = [—5,8) на числовой прямой.