Построение укрупненного статического ряда

Определение систематической погрешности.

В общем случае, если известна величина Z, воздействующая на прибор, с точностью в три и более раз превышающей точность самого прибора (например, образцовая, эталонная), то систематическую погрешность определяем по формуле 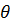= 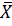-Z

где 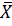- среднее арифметическое значение неисправленного ряда наблюдений, В

Среднее арифметическое значение неисправленного ряда наблюдений определяем по формуле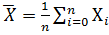

В нашем случае значение неисправленного ряда наблюдений:

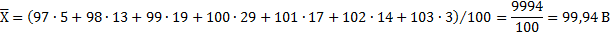
Тогда систематическая погрешность

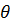=99,94-100 = -0,06 В

Систематическая погрешность должна быть исключена из результатов измерений путём введения поправки, равной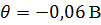

После введения поправки получается исправленный ряд значений

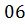97, ; 97, 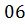; 97,06; 97,06; 97,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 103,06; 103,06; 103,06; В

Построение укрупненного статического ряда

Для удобства обработки результатов наблюдений построим укрупненный статический ряд.

Определяем область изменения признака (размах выборки):

R=X_max-X_min

где X_max и X_min – наибольшее и наименьшее показание прибора при измерениях

Для нашего примера

R=103,07-97,07=6 В

Определяем число классов (интервалов) укрупненного статического ряда m:

m_min=0,55n^0,4 m_max=1,25n^0,4

Для нашего примера

m_min=3,47 m_max=7,88

Рекомендуется брать нечетное число интервалов и не менее пяти. Примем m=7

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР. 52.12.38. 08

Определяем ширину класса (интервал):

d= , при условии dm≥R

Значение d округляем в большую сторону со значащими цифрами, как и у выборки (или в два раза точнее). В нашем случае точность оценки d может быть 1,0 и 0,5 В (примем 0,5). Тогда

d=6/7=0,86 тогда d=1,0 мА

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР. 52.12.38. 08

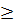Строим таблицу укрупненного статистического ряда (таблица 8.1). В первой строке таблицы записываем номера классов укрупненного ряда 1…j…m. Во второй строке располагаем наибольшее и наименьшее значение результатов наблюдений для каждого класса. Наименьшее значение первого класса приравниваем к наименьшему значению выборки: Xmin Ximin; наибольшее значение первого класса получается так: X₁min+d=Xjmax. Для всех классов последовательность выбора повторяем.

Номер класса m								Σ
Границы	Xj min	96,56	97,56	98,56	99,56	100,56	101,56	102,56	-
класса	Xj max	97,56	98,56	99,56	100,56	101,56	102,56	103,56	-
Средняя точка класса Xj	97,06	98,06	99,06	100,06	101,06	102,06	103,06	-
Частота nj
Относительная частота Nj	0,05	0,13	0,19	0,29	0,17	0,14	0,03
(Xj-X)	-2,94	-1,94	-0,94	0,06	1,06	2,06	3,06	-
Nj(Xj-X)²	0,43	0,49	0,17	0,0014	0,19	0,29	0,28	1,8514
Nj(Xj-X)³	-1,27	-0,95	-0,16	0,0000	0,2	1,2	0,86	-0,12
Nj(Xj-X)⁴	3,74	1,84	0,15	0,0000	0,22	2,52	2,63	11,1
tj	2,16	1,42	0,69	0,044	0,78	1,5	2,25	-
Нормальное распределение	P*(tj)	0,04	0,147	0,32	0,40	0,30	0,131	0,0325	-
Pj=(d/s)P*(tj)	0,029	0,11	0,24	0,29	0,222	0,097	0,024
Ej=Pjn	0,145	1,43	4,56	8,41	3,77	1,4	0,072
|(Ej-nj|)
(nj-Ej)²/Ej
Распределение Лапласа	P*(tj)
Pj=(d/s)P*(tj)
Ej=Pjn
|(Ej-nj|)
(Ej-nj)²/Ej
Распределение Симпсона	P*(Xj)
Pj=(d/s)P*(tj)
Ej=Pjn
|(Ej-nj|)
(Ej-nj)²/Ej

КР.53.12.38. 08

Лист

Таблица 8.3

Изм.

Лист

№ докум.№

Подпись

Дат

Лист

КР. 52.12.38. 08

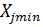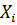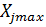Частота в nj в j-м классе – это попавшее в интервал ≤ ≤ значения 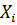выборка 1…i…n. Заполняется пятая строка таблицы 8.3 При этом сумма частот:

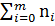=n

В нашем случае 4+9+22+28+20+12+5=100

Относительная частот N_j записываем в шестой строке таблицы и определяем так

N_j=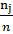

Поэтому 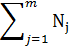=1,0