Матричный метод решения СЛАУ
Систему 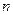 линейных алгебраических уравнений с
линейных алгебраических уравнений с 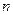 неизвестными и определителем основной матрицы А системы, отличным от нуля, можно решать с помощью обратной матрицы.
неизвестными и определителем основной матрицы А системы, отличным от нуля, можно решать с помощью обратной матрицы.
Пусть дана система уравнений (6.3), основная матрица А которой невырожденная. Система имеет единственное решение, которое можно найти по формуле:
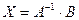 ,
,
где 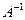 - матрица, обратная к А.
- матрица, обратная к А.
Пример. Решить систему предыдущего пункта матричным методом.
Решение. Данная система в матричной форме имеет вид 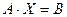 , где
, где 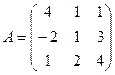 ,
, 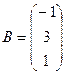 ,
, 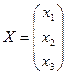 . Ее решение
. Ее решение 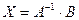 .
.
1) Находим обратную матрицу 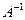 .
.
1. 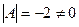
2. 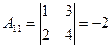 ,
, 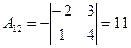 ,
, 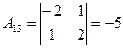 ,
,
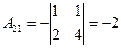 ,
, 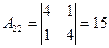 ,
, 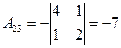 ,
,
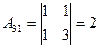 ,
, 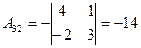 ,
, 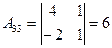
3. 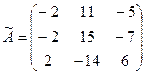
4. 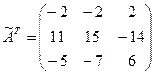
5. 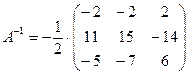
2) 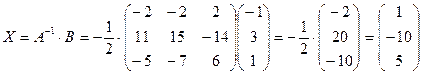
Ответ: 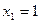 ,
, 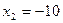 ,
, 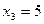 .
.
Решение и исследование систем линейных
алгебраических уравнений
Полный ответ на вопрос о существовании решения системы 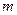 линейных уравнений с
линейных уравнений с 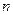 неизвестными дает следующая теорема Кронекера-Капелли.
неизвестными дает следующая теорема Кронекера-Капелли.
Для того чтобы система уравнений (6.1) была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы был равен рангу основной матрицы системы. Если ранги основной и расширенной матриц совпадают с числом неизвестных, то система имеет единственное решение. Если ранг 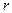 основной и расширенной матриц меньше числа неизвестных
основной и расширенной матриц меньше числа неизвестных 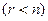 , то система (6.1) имеет бесконечное множество решений.
, то система (6.1) имеет бесконечное множество решений.
В последнем случае 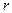 неизвестных назовем базисным, а
неизвестных назовем базисным, а 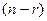 - свободными. Свободным неизвестным можно придавать произвольные значения, тогда оставшиеся
- свободными. Свободным неизвестным можно придавать произвольные значения, тогда оставшиеся 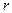 неизвестных определяются уже единственным образом.
неизвестных определяются уже единственным образом.
Метод Гаусса (метод последовательного исключения неизвестных).
Метод Гаусса состоит в том, что при помощи элементарных преобразований систему приводят к такому виду, чтобы ее расширенная матрица оказалась трапециевидной (ступенчатой). После этого уже не представляет труда разобраться в вопросе о совместности системы, определить число решений и найти сами решения.
Поясним идею метода Гаусса на примерах.
Пример. Решить систему 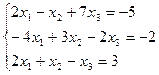 .
.
Решение. Выписываем расширенную матрицу системы. С помощью элементарных преобразований приведем матрицу к ступенчатому виду
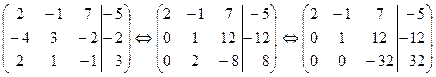
Если не учитывать последний столбец, найдем ранг основной матрицы 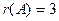 ; учитывая последней столбец, найдем ранг расширенной матрицы
; учитывая последней столбец, найдем ранг расширенной матрицы 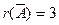 . Число неизвестных тоже равно 3. Система совместна и имеет единственное решение. Полученной матрице соответствует эквивалентная система:
. Число неизвестных тоже равно 3. Система совместна и имеет единственное решение. Полученной матрице соответствует эквивалентная система:
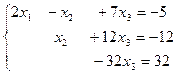
Далее порядок действий очевиден. Из последнего уравнения 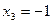 ; подставляя это значение во второе уравнение, мы получаем
; подставляя это значение во второе уравнение, мы получаем 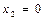 . И наконец, из первого уравнения находим
. И наконец, из первого уравнения находим 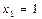 .
.
Замечания. При переходе от первой матрицы ко второй в качестве рабочей строки бралась первая, которая умножалась соответственно на 2 и (-1) и складывалась со второй и третьей строками. В результате мы получили нули в первом столбце. При переходе от второй матрицы к третьей в качестве рабочей строки бралась вторая, которая умножалась на (-2) и складывалась с третьей строкой.
Пример. Исследовать систему 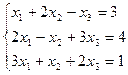 .
.
Решение.
Составим расширенную матрицу и приведем ее к ступенчатому виду.
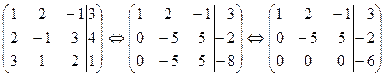
Так как 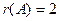 ,
, 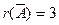 , то система несовместна.
, то система несовместна.
Пример. Решить систему 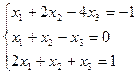 .
.
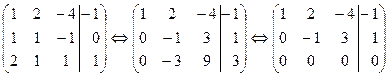
Так как 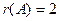 ,
, 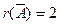 , то система совместна. Она имеет бесчисленное множество решений, потому что ранг матрицы меньше числа неизвестных. Восстановим систему по последней матрице:
, то система совместна. Она имеет бесчисленное множество решений, потому что ранг матрицы меньше числа неизвестных. Восстановим систему по последней матрице:
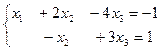
Базисными неизвестными являются 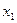 и
и 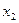 , переменная
, переменная 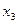 - свободной. Обратной подстановкой найдем
- свободной. Обратной подстановкой найдем 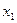 и
и 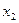 из системы:
из системы:
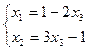 ,
,
где 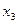 - любое действительное число.
- любое действительное число.
