Покажемо, що М-абелева група відносно операції додавання. 2 страница
Оскільки кожен вектор із 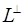 є лінійною комбінацією базису, то
є лінійною комбінацією базису, то 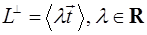 .
.
в) знайдемо відповідно проекції 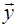 і
і 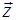 вектора
вектора 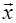 на підпростори
на підпростори 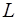 і
і 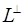 .
.
Оскільки 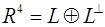 , то вектор
, то вектор 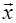 має єдине зображення
має єдине зображення 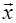 =
= 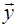 +
+ 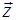 , де
, де 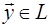 ,
, 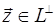 .
.
Враховуючи, що L – лінійна оболонка, натягнута на вектори 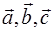 , маємо
, маємо
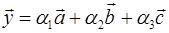 , тоді
, тоді
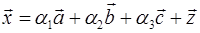 (*).
(*).
Обидві частини рівності (*) скалярно помножуємо на вектори 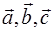 , і враховуючи, що (
, і враховуючи, що ( 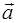 ,
, 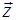 ) = (
) = ( 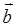 ,
, 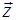 ) = (
) = ( 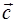 ,
, 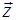 ) = 0, маємо:
) = 0, маємо:
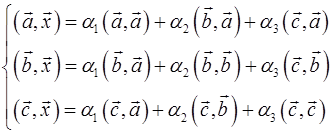
Одержуємо систему рівнянь:
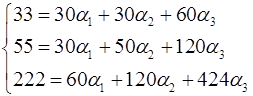 або
або 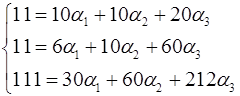
розв’язуючи систему рівнянь, знаходимо:
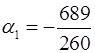 ;
; 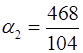 ;
; 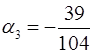 .
.
Отже, 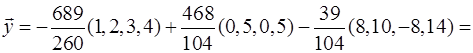
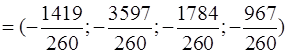
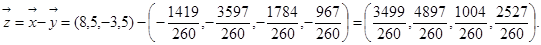
Отже, проекція 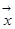 на L:
на L: 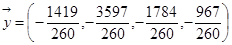 , проекція
, проекція 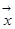 на
на 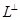 :
: 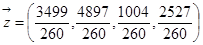 .
.
г) Оскільки 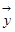 - проекція вектора
- проекція вектора 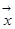 на підпростір L, обчислюємо за формулою:
на підпростір L, обчислюємо за формулою:
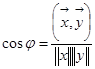


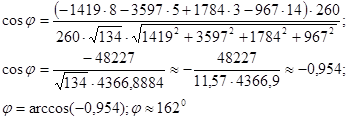
д) Відстань 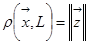
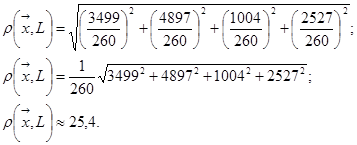
VI. Довести, що множення кожної квадратичної матриці другого порядку з дійсними коефіцієнтами зліва на матрицю 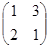 є лінійним оператором векторного простору всіх квадратичних матриць другого порядку над полем дійсних чисел R.
є лінійним оператором векторного простору всіх квадратичних матриць другого порядку над полем дійсних чисел R.
Знайти матрицю цього лінійного оператора у базисі із матриць
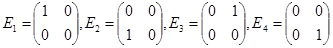
Розв’язання. Нехай A-оператор множення кожної квадратичної матриці другого порядку зліва на матрицю 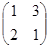 . Перевіряємо, чи буде він лінійним. Розглянемо образ суми двох матриць Х і У, де
. Перевіряємо, чи буде він лінійним. Розглянемо образ суми двох матриць Х і У, де 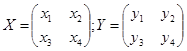 . Маємо
. Маємо 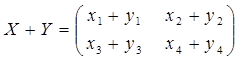
A (X+Y) 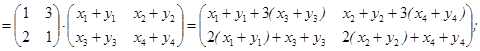
A X 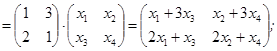
A Y 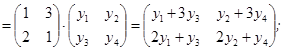
A X+A Y 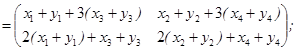
Отже, A (X+Y)= A X+A Y.
Нехай тепер 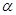 -довільне ціле число. Тоді A (
-довільне ціле число. Тоді A ( 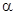 X)
X) 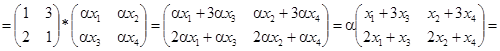
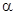 (A X)
(A X)
Звідси випливає: оператор A – лінійний.
Знайдемо його матрицю в заданому базисі.
Для цього знаходимо образи базисних векторів під дією оператора A.
A 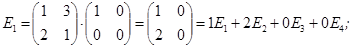
A 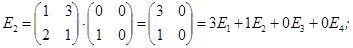
A 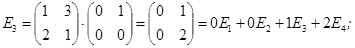
A 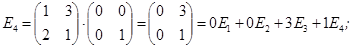
Матрицею А лінійного оператора A буде матриця
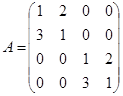
VII. Нехай лінійний оператор A в базисі 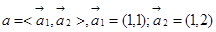 має матрицю
має матрицю 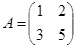 , а лінійний оператор B в базисі
, а лінійний оператор B в базисі 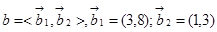 має матрицю
має матрицю 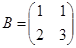 . Знайти матрицю Х лінійного оператора A B в базисі, в якому задано координати всіх векторів.
. Знайти матрицю Х лінійного оператора A B в базисі, в якому задано координати всіх векторів.
Розв’язання. Позначимо матрицю лінійного оператора A в базисі e, в якому задані координати всіх векторів, через 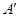 , а оператора B – через
, а оператора B – через 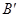 . Тоді
. Тоді 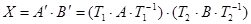 , де T1 і T2 – матриці переходів від базисів a i b до базису e відповідно. Оскільки матриці
, де T1 і T2 – матриці переходів від базисів a i b до базису e відповідно. Оскільки матриці 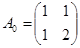 і
і 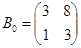 , рядками яких є координати векторів базисів a i b відповідно, є матрицями переходу від базису е до базисів a i b, то
, рядками яких є координати векторів базисів a i b відповідно, є матрицями переходу від базису е до базисів a i b, то 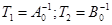 ,
,
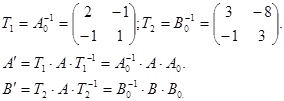
Виконаємо обчислення:
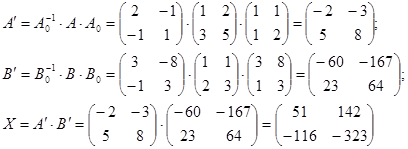
Відповідь: 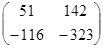 .
.
VIII. Побудувати ядро KerA, область значень ImA та знайти ранг 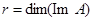 , дефект
, дефект 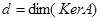 лінійного оператора A -векторного простору L3, який у деякому базисі цього простору
лінійного оператора A -векторного простору L3, який у деякому базисі цього простору 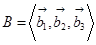 задано матрицею
задано матрицею 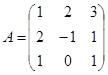 .
.
Розв’язання. Оскільки ранг лінійного оператора A дорівнює рангу матриці А, знайдемо r(A): 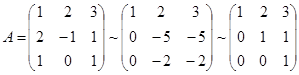 . Звідси r(A)=2, і тому dim(ImA )=2, тобто ранг лінійного оператора A дорівнює 22. Виходячи з рівності dim(ImA )+dim(KerA )=n, одержуємо dim(KerA )=3–2=1, тобто дефект лінійного оператора А дорівнює 1. Для побудови KerA і ImA достатньо знайти їх базиси.
. Звідси r(A)=2, і тому dim(ImA )=2, тобто ранг лінійного оператора A дорівнює 22. Виходячи з рівності dim(ImA )+dim(KerA )=n, одержуємо dim(KerA )=3–2=1, тобто дефект лінійного оператора А дорівнює 1. Для побудови KerA і ImA достатньо знайти їх базиси.
Оскільки ImA = < xA 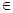 R3 >,
R3 >, 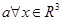 ,
, 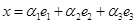 ,
, 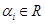 , то підпростір
, то підпростір 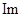 породжується системою векторів e1A, e2A, e3A.
породжується системою векторів e1A, e2A, e3A.
Знаходимо ці вектори:
e1A =(1,2,3); e2A =(2,–1,1); e3A =(1,0,1).
Ранг цієї системи векторів дорівнює r(A)=2, отже, максимальна лінійно незалежна підсистема цієї системи векторів складається з двох векторів. За цю систему можна взяти вектори e1A і e2A ; отже, ImA складається з векторів e1A =(1,2,3); e2A =(2,–1,1).Тоді ImA 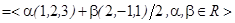 .
.
Побудуємо KerA. Оскільки KerA 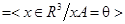 , то KerA є множина тих векторів простору R3, координатні рядки яких у базисі
, то KerA є множина тих векторів простору R3, координатні рядки яких у базисі 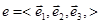 утворюють простір розв’язків системи лінійних однорідних рівнянь [x]A=[
утворюють простір розв’язків системи лінійних однорідних рівнянь [x]A=[ 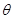 ], або
], або
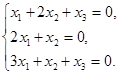
Оскільки матриця цієї системи є матрицею, транспонованою до матриці А, то ранг цієї системи дорівнює 2. За вільне невідоме обираємо х1. Тоді 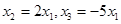 , і фундаментальною системою розв’язків підпростору розв’язків цієї системи є вектор
, і фундаментальною системою розв’язків підпростору розв’язків цієї системи є вектор 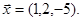
Тоді Ker A 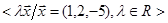 .
.
Відповідь: ImA 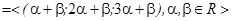 . KerA
. KerA 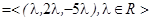 .
. 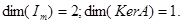 dim(ImA )=2; dim(KerA )=1.
dim(ImA )=2; dim(KerA )=1.
IX. Знайти власні значення і власні вектори лінійного оператора A, заданого в деякому базисі B=<b1,b2,b3> цього простору матрицею 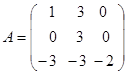
Розв’язання.
Характеристичне рівняння оператора, заданого матрицею А має вигляд
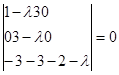
Розв’язавши його, одержуємо 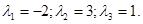
Усі корені – дійсні числа, отже лінійний оператор має три власних значення:
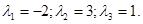
Знайдемо власні векторі, що відповідають цим значенням.
Нехай 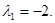 Маємо наступну систему лінійних однорідних рівнянь:
Маємо наступну систему лінійних однорідних рівнянь:
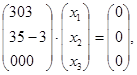 або
або 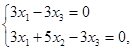 r=2;
r=2;
Фундаментальна система розв’язків складається із одного вектора 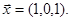
Отже, всі власні вектори, що належать власному значенню 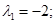 мають вигляд
мають вигляд
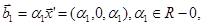
тобто всі ненульові вектори, що належать підпростору L1, що натягнутий на вектор (1,0,1).
Для 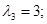 маємо наступну систему лінійних однорідних рівнянь.
маємо наступну систему лінійних однорідних рівнянь.
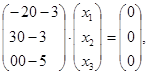 або
або
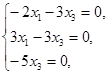 r=2
r=2
Фундаментальна система розв’язків складається з одного вектора x”=(0,1,0), тоді всі власні вектори, що належать власному значенню 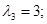 мають вигляд
мають вигляд
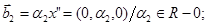
тобто, всі ненульові вектори, які належать підпростору, натягнутому на вектор (0,1,0).
Для 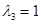 маємо систему рівнянь:
маємо систему рівнянь:
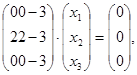 або
або
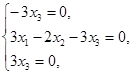 r=2.
r=2.
Фундаментальна система розв’язків є вектор
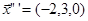 .
.
Тоді власні вектори, що належать власному значенню 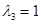 , мають вигляд:
, мають вигляд:
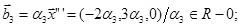
Тобто всі ненульові вектори, що належать підпростору L2, натягнутому на вектор (-2,3,0).
Отже, лінійний оператор, заданий матрицею А, має три різних власних значення і відповідні ним власні вектори, ненульові вектори з лінійних оболонок L1,L2,L3, натягнутих на вектора (1,0,1), (0,1,0), (-2,3,0).
Х. Чи зводиться матриця 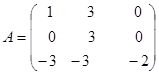 лінійного оператора A векторного простору V3 до діагонального вигляду за допомогою переходу до іншого базису? Знайти цей базис і відповідну йому матрицю.
лінійного оператора A векторного простору V3 до діагонального вигляду за допомогою переходу до іншого базису? Знайти цей базис і відповідну йому матрицю.
Розв’язання. Достатньою умовою для зведення матриці лінійного оператора векторного простору розмірності n є наявність у даного оператора n різних власних значень (оператор повинен мати простий спектр), причому діагональними елементами будуть саме ці власні значення.
У матриці А всі власні значення різні і їх три: 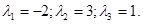
Отже, матриця А зводиться до діагональної матриці
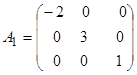 .
.
Визначимо базис, в якому матриця А має діагональний вид А1.
Оскільки цей процес зводиться до знаходження власних векторів оператора, то маємо такий базис для матриці А1:
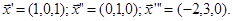
Відповідь: 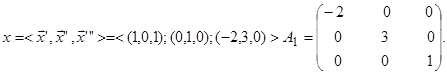
Контрольна робота № 4
І. Для квадратичної форми  f знайти:
f знайти:
а) матрицю та її ранг;
б) записати форму f у матричному вигляді;
в) методом Лагранжа привести форму f до нормального виду;
г) знайти лінійне перетворення, що приводить форму f до
нормального виду;
д) з’ясувати, чи є форма f позитивно визначеною.
1. f=x12+5x22+4x32-2x1x2+4x1x3;
2. f=4x12+4x22+x32-4x1x2+4x1x3-3x2x3;
3. f=x12-3x32+2x1x2-6x2x3;
4. f=7x12+6x22+5x32-4x1x2-4x2x3 ;
5. f=6x12-2x22+6x32+4x1x3;
6. f=2x12+5x22+x32+2x1x2+2x2x3-16x1x3;
7. f=x12-2x22+3x32+4x1x2-4x2x3-8x1x3;
8. f=2x1x2+3x2x3-x1x3;
9. f=5x1x2-x2x3+x1x3;
10. f=4x12+5x22+6x32-4x1x2+4x2x3.
II.Запишіть квадратичні форми з матрицею А, якщо
1. A= 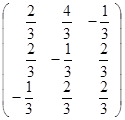 ; 2. A=
; 2. A= 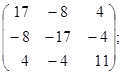 3. A=
3. A= 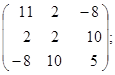
4. A= 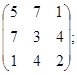
 5. A=
5. A= 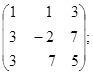 6. A=
6. A= 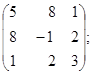
7. A= 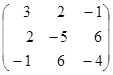 ; 8. A=
; 8. A= 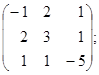 9. A=
9. A= 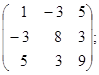
10. A= 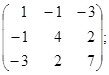
Знайти ортогональні перетворення, що приводять квадратичні форми задані в евклідовому просторі 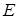 3 до канонічного виду. Записати цей канонічний вид.
3 до канонічного виду. Записати цей канонічний вид.
1. f=2x1x2+x22+x12+x3 2 +4x1x3+2x2x3;
2. f=11x12+5x22+2x32+16x1x2+4x1x3-20x2x3;
3. f=x12+x22+5x32-6x1x2+6x1x3 –6x2x3;
4. f=x12+x22+x32+4x1x2+4x1 x3+42x3;
5. f=17x12+14x22+14x32 –4x1 x2-4x 1x3-8x2 x3;
6. f=6x12+5x22+7x32-4x1x2+4x1x3 ;
7. f=4x12+x22+x32-4x1x2+4x 1x3-3x2x3;
8. f=x12+2x22+3x32-4x1x2-4x2x3;
9. f=2x12+x22-4x1x2-4x2x3;
10. f=5x12+7x22+6x32-4x1x3+4x2x3.
IV. Записати канонічне рівняння поверхні другого порядку, визначити її тип та знайти канонічну систему координат.
1. x12+y2+z32+2xy+4xz+2yz-6x+8y-2z-5=0;
2. 11x2+5y2+2z2+16xy+4xz-20yz+4x-6y+8z+1=0;
3. x12+y2+5z2-6xy+6xz-6yz-2x+4y-6z-4=0;
4. x2+y2+z2+4xy+4xz+4yz-6x+4y-2z-1=0;
5. 17x2+14y2+14z2-4xy-4xz-8yz-2x+6y-8z-4=0;
6. 6x2+5y2+7z2-4xy+4xz-8x+2y-2z+3=0;
7. 4x2+y2+z2-4xy+4xz-3yz+4y-6z+2y-4=0;
8. x2+2y2+3z2-4xy-4yz+2y+4z-2x+1=0;
9. 2x2+y2-4xy-4yz+2x-2y+6z-2=0;
10. 5x2+7y2+6z2-4xz+4yz-4x-2y+8z-2=0;
Зразки розв’язання задач контрольної роботи № 4
І. Для квадратичної форми f знайти:
а) матрицю та її ранг;
б) записати квадратичну форму у матричному вигляді;
в) методом Лагранжа привести форму f до нормального виду;
г) знайти лінійне перетворення, що приводить форму f до
нормального виду;
д) з’ясувати, чи є форма f позитивно визначеною.
Розв’язання:
Нехай f=2x1x2-12x1x3-x22-8x32;
а) Знаходимо матрицю А форми f:
A= 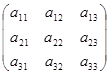 =
= 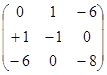
Обчислюємо ранг матриці А.
A= 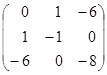 ~
~ 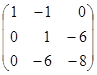 ~
~ 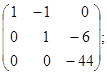 r=3.
r=3.
б) Запишемо квадратичну форму f у матричному вигляді:
Нехай Х= 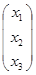 , тоді XT=(х1,х2,х3) і f=XT·A·X
, тоді XT=(х1,х2,х3) і f=XT·A·X
Дійсно, ХТ·А·Х=(х1,х2,х3)· 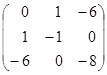 ·
· 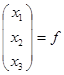 .
.
в) Методом Лагранжа перетворюємо квадратичну форму f до нормального виду.
1-е перетворення: 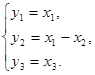
За допомогою 1-го перетворення виділяємо квадрат невідомого х2.
Матриця цього перетворення Q= 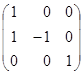 .
.
Знаходимо матрицю, обернену до матриці Q
Q/E= 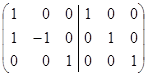 ~
~ 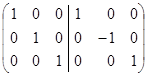
отже, G-1= 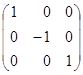 , тоді (Q-1)T=
, тоді (Q-1)T= 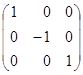
Знаходимо матрицю форми f1, яка одержується з матриці форми f в результаті лінійного перетворення з матрицею Q:
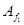 =
= 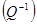 T·Af ·Q-1
T·Af ·Q-1
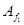 =
= 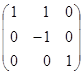 ·
· 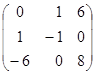 ·
· 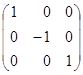 =
= 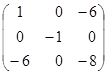 .
.
За одержаною матрицею записуємо формулу f1:
f1=y12-y22-8y32-12y1y3.
2- перетворення:
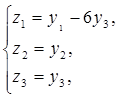 , за допомогою якого виділяємо
, за допомогою якого виділяємо
квадрат невідомого у1. Його матриця 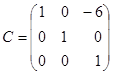 .
.
Знаходимо 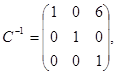 тоді
тоді 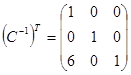 .
.
Обчислюємо матрицю 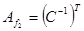 ·
· 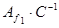 .
.
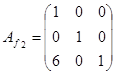 ·
· 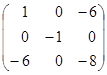 ·
· 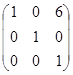 =
= 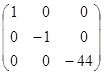 .
.
Матриці 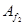 відповідає квадратична форма f2:
відповідає квадратична форма f2:
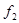 =z12-z22-44z32, яка має канонічний вид.
=z12-z22-44z32, яка має канонічний вид.
Зводимо форму f2 до нормального виду за допомогою лінійного перетворення: 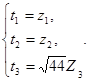 Його матриця
Його матриця 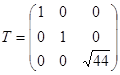 , тоді
, тоді 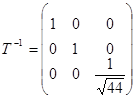 .
.
Тоді 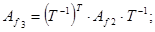
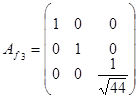 ·
· 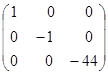 ·
· 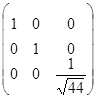 =
= 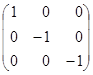 .
.
Отже, f3=t12-t22-t32 – нормальний вид форми f.
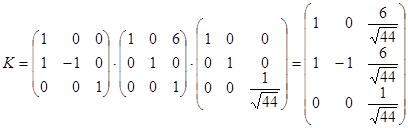 ,
,
тоді