Задачи для самостоятельного решения. 1. Тело брошено со скоростью под углом к горизонту
1. Тело брошено со скоростью 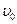 под углом к горизонту. Время полета
под углом к горизонту. Время полета 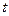 = 2,20 с. На какую высоту h поднимется тело? (Ответ: h = 5,9 м)
= 2,20 с. На какую высоту h поднимется тело? (Ответ: h = 5,9 м)
2. Точка движется по окружности радиусом.R = 2,00 см. Зависимость пути от времени дается уравнением 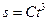 , где С = 0,1000 см /с3. Найти нормальное
, где С = 0,1000 см /с3. Найти нормальное 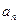 и тангенциальное
и тангенциальное 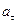 ускорения точки в момент, когда линейная скорость точки
ускорения точки в момент, когда линейная скорость точки 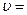 0,300 м /с. (Ответ:
0,300 м /с. (Ответ: 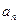 = 4,50 м/с2;
= 4,50 м/с2; 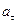 = 0,060 м/с2)
= 0,060 м/с2)
3. Стальная проволока выдерживает силу натяжения Е = 4.40 кН. С каким наибольшим ускорением 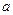 можно поднимать груз массой т = 400.г, подвешенный на этой проволоке, чтобы она не разорвалась? (Ответ: а=1,25 м/с2)
можно поднимать груз массой т = 400.г, подвешенный на этой проволоке, чтобы она не разорвалась? (Ответ: а=1,25 м/с2)
4. Поезд массой т = 500 т. двигаясь равнозамедленно, в течение времени t=1,00 мин уменьшает свою скорость от 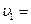 40 км/ч до
40 км/ч до 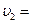 28 км/ч. Найти силу торможения F. (Ответ: F = 28 кН)
28 км/ч. Найти силу торможения F. (Ответ: F = 28 кН)
5. Какую силу F надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за время t=30,0 с прошел путь 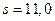 м? Масса вагона т = 16,0 т, Во время движения на вагон действует сила трения
м? Масса вагона т = 16,0 т, Во время движения на вагон действует сила трения 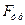 , равная 0,0500 действующейна него силытяжести
, равная 0,0500 действующейна него силытяжести 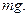 (Ответ: F= 8,2 кН)
(Ответ: F= 8,2 кН)
6. Молекула массой т=4,65*10-26 кг, летящая со скоростью 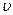 = 600 м/с, ударяется о стенку сосуда под углом
= 600 м/с, ударяется о стенку сосуда под углом 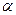 = 60° к нормали и упруго отскакивает от нее без потери скорости. Найти импульс, полученный стенкой за время удара. (Ответ:
= 60° к нормали и упруго отскакивает от нее без потери скорости. Найти импульс, полученный стенкой за время удара. (Ответ: 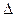 Р = 2,8*10-23кг м / с)
Р = 2,8*10-23кг м / с)
7. На автомобиль массой т=1т во время движения, действует сила трения 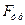 , равная 0,1 действующей на него силы тяжести
, равная 0,1 действующей на него силы тяжести 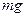 . Найти силу тяги F, развиваемую мотором автомобиля, если автомобиль движется с ускорением а=1 м/с2 в гору с уклоном 1 м на каждые 25 м-пути. (Ответ F=2,37 кН)
. Найти силу тяги F, развиваемую мотором автомобиля, если автомобиль движется с ускорением а=1 м/с2 в гору с уклоном 1 м на каждые 25 м-пути. (Ответ F=2,37 кН)
8. Тело скользит сначала вниз по наклонной плоскости, составляющей угол 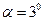 с горизонтом, а затем по горизонтальной поверхности. Найти коэффициент трения k на всем пути, если известно, что тело проходит по горизонтальной поверхности то же расстояние, что и по наклонной плоскости. (Ответ: k=0,07)
с горизонтом, а затем по горизонтальной поверхности. Найти коэффициент трения k на всем пути, если известно, что тело проходит по горизонтальной поверхности то же расстояние, что и по наклонной плоскости. (Ответ: k=0,07)
9. Два шара движутся навстречу друг другу и соударяются абсолютно не упруго. Скорости шаров до удара были 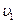 = 2 м/с и
= 2 м/с и 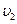 = 4 м/с. Общая скорость шаров после удара и = 1 м/с и по направлению совпадает с направлением скорости
= 4 м/с. Общая скорость шаров после удара и = 1 м/с и по направлению совпадает с направлением скорости 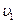 Во сколько раз кинетическая энергия
Во сколько раз кинетическая энергия 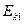 первого шара была больше кинетической
первого шара была больше кинетической 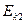 энергии второго шара? (Ответ:
энергии второго шара? (Ответ: 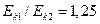 ).
).
10. Движущийся шар массой 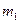 , ударяется о неподвижный шар массой
, ударяется о неподвижный шар массой 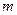 2. Каким должно быть отношение масс
2. Каким должно быть отношение масс 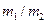 , чтобы при центральном абсолютно упругом ударе скорость первого шара уменьшилась в 1,5 раза? С какой кинетической энергией Е начнет двигаться при этом второй шар, если первоначальная кинетическая энергия первого шара
, чтобы при центральном абсолютно упругом ударе скорость первого шара уменьшилась в 1,5 раза? С какой кинетической энергией Е начнет двигаться при этом второй шар, если первоначальная кинетическая энергия первого шара 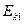 =1кДж? (Ответ:
=1кДж? (Ответ: 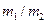 =5; ЕК2 = 5/9кДж)
=5; ЕК2 = 5/9кДж)
11. Диск вращается вокруг вертикальной оси счастотой п = 30 об/мин. На расстоянии 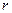 = 20 см от оси вращения на диске лежит тело. Каким должен быть коэффициент трения k между телом и диском, чтобы тело не скатилось с диска? (Ответ: k=0,2)
= 20 см от оси вращения на диске лежит тело. Каким должен быть коэффициент трения k между телом и диском, чтобы тело не скатилось с диска? (Ответ: k=0,2)
12. Найти вторую космическую скорость 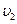 , т.е. скорость, которую надо сообщить телу у поверхности Земли, чтобы оно преодолело земное тяготение и навсегда удалилось от Земли. (Ответ:
, т.е. скорость, которую надо сообщить телу у поверхности Земли, чтобы оно преодолело земное тяготение и навсегда удалилось от Земли. (Ответ: 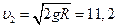 км/с)
км/с)
13. Диск массой т=2 кг катится без скольжения по горизонтальной плоскости со скоростью 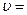 4 м/с. Найти кинетическую энергию Ек диска. (Ответ
4 м/с. Найти кинетическую энергию Ек диска. (Ответ 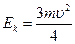 =24,0 Дж)
=24,0 Дж)
14. Какую работу А совершает человек при переходе от края платформы к ее центру в условиях предыдущей задачи? Радиус платформы R=1,5м. (Ответ: А = 162Дж)
15. Точка движется по окружности радиусом 4 м. Закон ее движения выражается уравнением 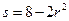 , где s - в метрах,
, где s - в метрах, 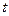 - в секундах. Найти: 1) в какой момент времени нормальное ускорение тощей будет
- в секундах. Найти: 1) в какой момент времени нормальное ускорение тощей будет 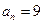 м/с2; 2) чему равны скорость, тангенциальное и полное ускорения точки в этот момент времени?(Ответ: 1,5 с: - 6 м/с; - 4 м/с2; 9,84 м/с2)
м/с2; 2) чему равны скорость, тангенциальное и полное ускорения точки в этот момент времени?(Ответ: 1,5 с: - 6 м/с; - 4 м/с2; 9,84 м/с2)
16. Две материальные точки движутся согласно уравнениям
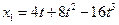 и
и 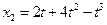 ,
,
где х - в метрах, t - .в секундах. В какой момент времени ускорения этих точек будут одинаковыми? Найти скорость точек в этот момент. (Ответ:0.235 с; 5,10 м/с ; 0,286 м /с )
17. Через блок, выполненный в виде колеса, перекинута нить, к концам которой привязаны грузы с массами m1 = 1 00 г и m2 = 300 г. Массу колеса М=200 г считать равномерно распределенной по его ободу, массой спиц пренебречь. Определить: 1) ускорение, с которым будут двигаться грузы; 2) силы натяжения нити по обе стороны блока. (Ответ: 3.27 м/с2; 1,31 Н; 1,96 Н)
18. Двум одинаковым маховикам, находящимся в покое, сообщили одинаковую угловую скорость 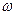 = 10 об/с и предоставили их самим себе. Под действием сил трения первый маховик остановился через одну минуту, а второй сделал до полной остановки N = 360 оборотов. У какого маховика тормозящий момент был больше и во сколько раз? (Ответ: у первого больше в 1,2 раза)
= 10 об/с и предоставили их самим себе. Под действием сил трения первый маховик остановился через одну минуту, а второй сделал до полной остановки N = 360 оборотов. У какого маховика тормозящий момент был больше и во сколько раз? (Ответ: у первого больше в 1,2 раза)
больше в 1,2 раза)
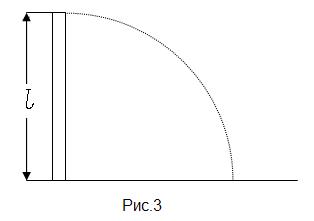 19. Платформа в виде диска вращается по инерции около вертикальной оси, делая
19. Платформа в виде диска вращается по инерции около вертикальной оси, делая 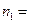 15 об/мин. На краю платформы стоит человек. Когда человек перешел в центр платформы, она стала делать п2 = 25 об/мин. Масса человека т=70 кг. Определить массу М платформы. Момент инерции человека рассчитывать как для материальной точки. (Ответ: 210 кг)
15 об/мин. На краю платформы стоит человек. Когда человек перешел в центр платформы, она стала делать п2 = 25 об/мин. Масса человека т=70 кг. Определить массу М платформы. Момент инерции человека рассчитывать как для материальной точки. (Ответ: 210 кг)
20. Стержень, нижний конец которого скользит по горизонтальной плоскости, падает из вертикального положения. С какой скоростью упадет на землю верхний конец, если 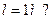 (Ответ:
(Ответ: 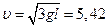 м/с)
м/с)
2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Единицы тепловых величин
Для получения производных единиц тепловых величин в системе СИ используются основные единицы: метр (м), килограмм (кг), секунда (с), кельвин (К).
В табл. 11 и 12 приводятся важнейшие производные единицы тепловых величин в системе СИ, а также внесистемные единицы, основанные на калории.
Единицы молярных величин образуются из перечисленных в табл. 11 и 12 единиц удельных величин шлем замены в них килограмма молем.
Таблица 11.
| Величина | Единица | Размерность величины | ||
| определение | наименование | обозначение | ||
| Количество теплоты | 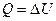 | джоуль | Дж | 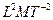 |
| Теплоемкость системы | 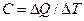 | джоуль на кельвин | Дж/К | 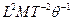 |
| Приращение энтропии при обратимом процессе системы | 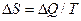 | джоуль на кельвин | Дж/К | 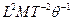 |
| Удельная теплоемкость | 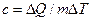 | джоуль на килограмм кельвин | Дж/(кг К) | 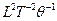 |
| Удельная энтропия | 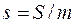 | джоуль на килограмм кельвин | Дж/(кг К) | 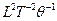 |
| Удельная теплота фазового превращения | 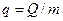 | джоуль на килограмм | Дж/кг | 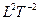 |
| Модуль градиента температуры | 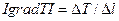 | кельвин на метр | К/м | 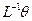 |
| Тепловой поток | 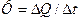 | ватт | Вт | 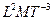 |
| Плотность теплового потока | 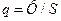 | ватт на квадратный метр | Вт/м2 | 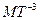 |
| Теплопроводность | 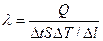 | ватт на метр кельвин | Вт/(м К) | 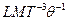 |
| Температуро-проводимость | 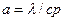 | квадратный метр в секунду | м2/с | 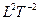 |
| Коэффициент теплообмена | 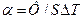 | ватт на квадратный метр-кельвин | Вт/(м2 К) | 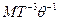 |
Таблица 12.
| Величина | Единица и её связь с единицами СИ |
| Количество теплоты | 1кал=4,19Дж |
| Теплоемкость системы; энтропия системы | 1кал=4,19Дж/К |
| Удельная теплоемкость; удельная энтропия | 1кал/(г К)=4,19*103Дж/(кг К) |
| Удельная теплота фазового превращения | 1кал/г=4,19*103Дж/кг |
| Тепловой поток | 1кал/с=4,19Вт |
| Плотность теплового потока | 1кал/(с см)=4,19*104Вт/м2 |
| Теплопроводность | 1кал/(с см К)=4,19*102Вт/(м К) |
Основные формулы
Идеальные газы подчиняются уравнению состояния 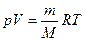 , гдг р - давление газа, V - его объем. Т - термодинамическая температура, m -масса газа, М - молярная масса газа, R = 8.31441 Дж /(моль * К ) - газовая постоянная: отношение v = m/М дает количество газа.
, гдг р - давление газа, V - его объем. Т - термодинамическая температура, m -масса газа, М - молярная масса газа, R = 8.31441 Дж /(моль * К ) - газовая постоянная: отношение v = m/М дает количество газа.
По закону Дальтона давление смеси газов равно сумме их парциальных давлений, т.е. тех давлений, которые имел бы каждый из газов в отдельности, если бы он при данной температуре один заполнял весь объем.
Основное уравнение кинетической теории газов имеет вид
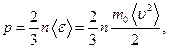
где п - число молекул в единице объема, 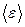 -средняя кинетическая энергия поступательного движения одной молекулы,
-средняя кинетическая энергия поступательного движения одной молекулы, 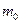 - масса молекулы,
- масса молекулы, 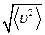 -средняя квадратичная скорость молекул. Эти величины определяются следующими формулами: число молекул в единице объема
-средняя квадратичная скорость молекул. Эти величины определяются следующими формулами: число молекул в единице объема 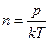 , где
, где 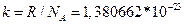 Дж/К - постоянная Больцмана,
Дж/К - постоянная Больцмана, 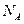 = 6,022045*1023 моль-1 - постоянная Авогадро; средняя кинетическая энергия поступательного движения одной молекулы
= 6,022045*1023 моль-1 - постоянная Авогадро; средняя кинетическая энергия поступательного движения одной молекулы 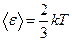 , средняя квадратичная скорость молекул
, средняя квадратичная скорость молекул 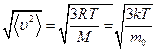 , причем
, причем 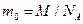 .
.
Внутренняя энергия газа 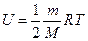 , где i- число степеней свободы молекул.
, где i- число степеней свободы молекул.
Связь между молярной С и удельной с теплоемкостями следует из определения: С = М с. Молярная теплоемкость газа при постоянном объеме 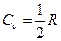 ;молярная теплоемкость при постоянном давлении
;молярная теплоемкость при постоянном давлении 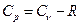 .
.
Отсюда следует, что молярная теплоемкость С определяется числом степеней свободы i молекул газа:
-для одноатомного газа (i=3) 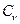 =12,5 Дж/(моль К),
=12,5 Дж/(моль К), 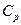 =20,8 Дж/(моль К);
=20,8 Дж/(моль К);
-для двухатомного газа (i=5) 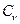 =20,8 Дж/(моль К),
=20,8 Дж/(моль К), 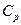 =29,1 Дж/(моль К);
=29,1 Дж/(моль К);
-для многоатомного газа 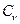 =24,9 Дж/(моль К),
=24,9 Дж/(моль К), 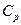 =33,2 Дж/(моль К).
=33,2 Дж/(моль К).
Закон распределения молекул по скоростям (закон Максвелла) позволяет найти число молекул 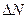 , относительно скорости которых лежат в интервале от и до и-
, относительно скорости которых лежат в интервале от и до и- 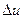 :
: 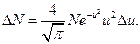 Здесь
Здесь 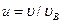 - относительная скорость,
- относительная скорость, 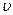 - данная скорость и
- данная скорость и 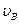
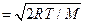 - наиболее вероятная скорость молекул,
- наиболее вероятная скорость молекул, 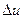 - интервал относительных скоростей, малый по сравнению со скоростью и.
- интервал относительных скоростей, малый по сравнению со скоростью и.
При решении задач на закон, распределения молекул по скоростям удобно пользоваться табл.13, в которой даны значения 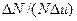 для различных и.
для различных и.
Таблица 13.
| и | 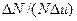 | и | 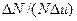 | и | 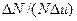 |
| 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 | 0,02 0,09 0,18 0,31 0,44 0,57 0,68 0,76 | 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 | 0,81 0,83 0,82 0,78 0,71 0,63 0,54 0,46 0,36 | 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 | 0,29 0,22 0,16 1,12 0,09 0,06 0,04 0,03 |
Средняя арифметическая скорость молекул 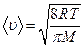 .
.
Во многих случаях важно знать число молекул 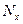 , скорости которых превышают заданное значение скорости
, скорости которых превышают заданное значение скорости 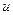 . В табл.14 даны значения
. В табл.14 даны значения 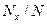 для различных
для различных 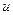 , где
, где 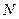 - общее число молекул.
- общее число молекул.
Таблица 14.
| и | 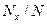 | и | 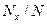 | и | 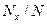 |
| 0,2 0,4 0,5 | 1,000 0,994 0,957 0,918 | 0,6 0,7 0,8 1,0 | 0,868 0,806 0,734 0,572 | 1,25 1,5 2,0 2,5 | 0,374 0,213 0,046 0,0057 |
Барометрическая формула дает закон убывания давления газа с высотой в поле силы тяжести: 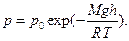 Здесь
Здесь 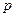 -давление газа на высоте h. р0 - давление на высоте
-давление газа на высоте h. р0 - давление на высоте 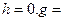 9,30665 м/с2 - ускорение свободного падения. Эта формула приближенная, так как получена в предположении, что Т не зависит от h.
9,30665 м/с2 - ускорение свободного падения. Эта формула приближенная, так как получена в предположении, что Т не зависит от h.
Средняя длина свободного пробега молекул газа
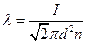 ,
,
где d - эффективный диаметр молекулы, п - число молекул в единице объема (концентрация молекул). Общее число столкновений всех молекул в единице объема за единицу времени 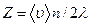 .
.
Масса, перенесенная за время 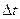 при диффузии,
при диффузии,
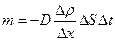 ,
,
где 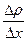 -градиент плотности в направлении, перпендикулярном к площадке
-градиент плотности в направлении, перпендикулярном к площадке 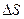 ,
, 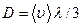 - коэффициент диффузии (
- коэффициент диффузии ( 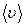 -средняя арифметическая скорость,
-средняя арифметическая скорость, 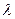 - средняя длина свободного пробега молекул).
- средняя длина свободного пробега молекул).
Сила внутреннего трения 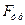 в газе:
в газе:
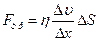 ,
,
где 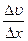 -градиент скорости течения газа в направлении, перпендикулярном к площадке
-градиент скорости течения газа в направлении, перпендикулярном к площадке 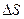 ,
, 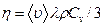 -динамическая вязкость.
-динамическая вязкость.
Количество теплоты, перенесенное за время 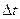 вследствие теплопроводности, определяется формулой
вследствие теплопроводности, определяется формулой 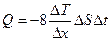 , где
, где 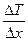 -градиент температуры в направлении, перпендикулярном к площадке
-градиент температуры в направлении, перпендикулярном к площадке 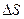 .
. 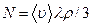 -теплопроводность.
-теплопроводность.
Первое начало термодинамики может быть записано в виде
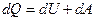 ,
,
где 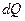 -количество теплоты, полученное газом,
-количество теплоты, полученное газом, 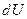 -приращение внутренней энергии газа, d А=р d V - работа, совершаемая газом. Внутренняя энергия газа
-приращение внутренней энергии газа, d А=р d V - работа, совершаемая газом. Внутренняя энергия газа
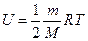 ,
,
где Т - термодинамическая температура. Работа, совершаемая газом, 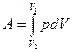 . Работа, совершаемая при изотермическом процессе,
. Работа, совершаемая при изотермическом процессе,
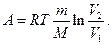
Давление и объем газа связаны при адиабатическом процессе уравнением Пуассона 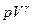 = const, где показатель адиабаты
= const, где показатель адиабаты 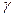 =
= 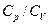 . Уравнение Пуассона может быть записано еще в таком виде:
. Уравнение Пуассона может быть записано еще в таком виде: 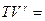 const.
const.
Работа, совершаемая при адиабатическом процессе, может быть найдена по формуле
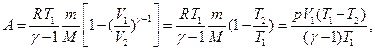
где 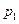 и
и 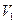 -давление и объем газа при температуре
-давление и объем газа при температуре 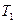 .
.
Уравнение политропического процесса имеет вид 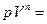 const, где
const, где 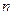 - показатель политропы (0 < п <
- показатель политропы (0 < п < 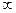 ).
).
Коэффициент полезного действия (КПД) тепловой машины
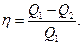
где Q1-количество теплоты, полученное рабочим телом от нагревателя. Q2 -количество теплоты, отданное холодильнику. Для цикла Карно
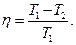
где 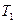 и
и 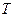 -термодинамические температуры нагревателя и холодильника. Разность энтропии SВ-SA двух состояний В и А определяется формулой
-термодинамические температуры нагревателя и холодильника. Разность энтропии SВ-SA двух состояний В и А определяется формулой
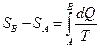 .
.
Реальные газы
Уравнение состояния реальных газов (уравнение Ван-дер-Ваальса) для одного моля газа имеет вид
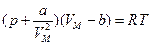 ,
,
где 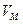 - молярный объем газа, а и b - постоянные, различные для разных газов, р - давление, Т - термодинамическая температура. R = 8,31411 Дж /(моль К) - газовая постоянная.
- молярный объем газа, а и b - постоянные, различные для разных газов, р - давление, Т - термодинамическая температура. R = 8,31411 Дж /(моль К) - газовая постоянная.
Уравнение Ван-дер-Ваальса для произвольной массы т газа имеет вид
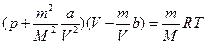 ,
,
где 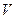 -объем газа. М - молярная масса газа. В этом уравнении
-объем газа. М - молярная масса газа. В этом уравнении 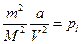 - давление, обусловленное силами взаимодействия молекул,
- давление, обусловленное силами взаимодействия молекул, 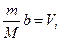 - объем, связанный с собственным объемом молекул.
- объем, связанный с собственным объемом молекул.
Постоянные а и Ь данного газа связаны с его критической температурой 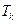 , критическим давлением рк и критическим молярным объемом
, критическим давлением рк и критическим молярным объемом 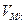 соотношениями
соотношениями
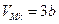 ,
, 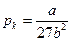 ,
, 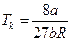 .
.
Эти уравнения можно решить относительно постоянных a и b:
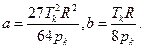
Если ввести относительные величины 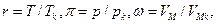 то уравнение Ван-дер-Ваальса для одного моля газа примет вид
то уравнение Ван-дер-Ваальса для одного моля газа примет вид
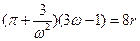 .
.
