Арианты индивидуальных заданий к лабораторной работе №2
абораторная работа №1
Построение математической модели методом наименьших квадратов (МНК)
Цель работы: освоение навыков построения математических моделей по экспериментальным данным с использованием метода наименьших квадратов.
Задание
1. В соответствии с присвоенным вариантом ознакомиться с заданием на лабораторную работу.
2. Занести исходные данные в бланк результатов лабораторной работы.
3. Рассчитать коэффициенты уравнения регрессии. При этом необходимые для вычисления величины внести в бланк результатов (см. пример из лекции 2).
4. Записать полученное выражение математической модели.
5. Определить коэффициент корреляции для проверки адекватности полученного уравнения регрессии экспериментальным данным.
6. Построить график кривой регрессии и нанести на него экспериментальные данные.
7. Используя математическую модель, для заданного значения входной величины вычислить значение выходной величины. Отобразить значения на графике.
8. Выполнить проверочный расчет с помощью программы, реализующей метод наименьших квадратов (файл mnk.xls). Распечатать результаты расчета. Сравнить результаты расчета по программе с результатами, полученными самостоятельно.
Содержание отчета
1. Заполненный бланк результатов расчета.
2. График кривой регрессии с нанесенными точками, соответствующими экспериментальным данным, а также заданного значения входной величины и соответствующего значения выходной величины.
3. Распечатанные результаты расчета по программе.
4. Вывод.
Лабораторная работа №1
Бланк результатов расчета
| Вариант | ||||||||||||
| Вид функциональной зависимости | Расчет коэффициента корреляции r | |||||||||||
| № | Исходные данные | xi × yi | xi2 | ypi | 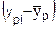 | 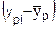 2 2 | 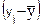 | 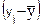 2 2 | 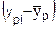 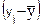 | |||
| xi | yi | |||||||||||
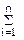 | ||||||||||||
 | ||||||||||||
 | ||||||||||||
| Полученное уравнение математической модели: | 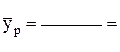 | 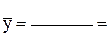 | ||||||||||
Коэффициент корреляции  | ||||||||||||
арианты индивидуальных заданий к лабораторной работе №1
Задание.Построить математическую модель вида y=a0 + a1x для тарировки тензодатчика по результатам измерений.
(Номер варианта соответствует номеру студента в списке группы)
| Вариант | Номер опыта | |||||
| xi (В) | 0,25 | 0,36 | 0,48 | 0,76 | 0,82 | |
| yi (кН) | ||||||
| xi (В) | 0,8 | 1,3 | 1,7 | 1,9 | 2,5 | |
| yi (кН) | 0,3 | 0,5 | 0,7 | 0,9 | 1,2 | |
| xi (В) | 1,7 | 2,2 | 2,5 | 3,2 | ||
| yi (кН) | 0,2 | 0,4 | 0,6 | 0,8 | ||
| xi (В) | 0,5 | 1,4 | 1,8 | 2,64 | 3,6 | |
| yi (кН) | 0,5 | 0,75 | 1,25 | 1,5 | ||
| xi (В) | 1,4 | 2,2 | 3,2 | |||
| yi (кН) | 0,25 | 0,5 | 0,75 | 1,0 | 1,25 | |
| xi (В) | 1,5 | 2,6 | 3,3 | 4,3 | ||
| yi (кН) | 1,25 | 1,5 | 1,75 | |||
| xi (В) | 0,8 | 1,4 | 2,5 | 3,7 | 4,6 | |
| yi (кН) | 1,2 | 1,4 | 1,6 | 1,8 | ||
| xi (В) | 0,2 | 0,6 | 1,3 | 1,8 | 2,4 | |
| yi (кН) | 1,25 | 1,75 | 2,25 | 2,75 | 3,25 | |
| xi (В) | 1,2 | 1,8 | 2,6 | 3,7 | 4,5 | |
| yi (кН) | 0,1 | 0,25 | 0,4 | 0,5 | 0,8 | |
| xi (В) | 1,5 | 2,4 | 3,2 | |||
| yi (кН) | 0,15 | 0,3 | 0,45 | 0,6 | 0,9 | |
| xi (В) | 2,3 | 2,7 | 3,6 | |||
| yi (кН) | 1,1 | 1,4 | 1,6 | 1,8 | ||
| xi (В) | 0,5 | 0,7 | 1,1 | 1,7 | ||
| yi (кН) | 0,3 | 0,6 | 0,9 | 1,2 | 1,5 | |
| xi (В) | 1,3 | 1,6 | 2,2 | 3,2 | ||
| yi (кН) | 0,15 | 0,2 | 0,25 | 0,5 | 0,8 | |
| xi (В) | 0,6 | 0,9 | 1,2 | 1,6 | 2,4 | |
| yi (кН) | 0,2 | 0,4 | 0,5 | 0,8 | 1,2 | |
| xi (В) | 1,6 | 2,3 | 2,7 | 3,4 | 4,1 | |
| yi (кН) | 0,7 | 0,9 | 1,2 | 1,5 | ||
| xi (В) | 1,2 | 1,5 | 2,4 | 3,1 | 3,8 | |
| yi (кН) | 0,2 | 0,3 | 0,6 | 0,9 | 1,4 | |
| xi (В) | 0,5 | 1,1 | 1,6 | 2,2 | 3,1 | |
| yi (кН) | 2,2 | 2,8 | 3,5 | |||
| xi (В) | 1,7 | 2,8 | ||||
| yi (кН) | 1,5 | 2,4 | 4,5 | |||
| xi (В) | 0,5 | 1,6 | 2,5 | 4,3 | ||
| yi (кН) | 2,3 | 2,5 | 3,4 | 4,2 | ||
| xi (В) | 0,4 | 0,8 | 1,6 | 2,3 | 3,2 | |
| yi (кН) | 1,5 | 2,5 | 3,5 | 4,2 |
абораторная работа №2
Построение математической модели методом планирования эксперимента
Цель работы: освоение навыков построения математических моделей с использованием метода планирования полного факторного эксперимента.
Задание
1. В соответствии с присвоенным вариантом ознакомиться с заданием на лабораторную работу.
2. Занести исходные данные в бланк результатов лабораторной работы.
3. Выполнить все необходимые вычисления (см. пример лекции 3-4).
4. Записать полученное выражение математической модели в кодированных и натуральных переменных.
5. Выполнить проверочный расчет с помощью программы, реализующей метод планирования эксперимента (файл plan.xls). Распечатать результаты расчета. Сравнить результаты расчета по программе с результатами, полученными самостоятельно.
Содержание отчета
1. Заполненный бланк результатов расчета.
2. График кривой регрессии с нанесенными точками, соответствующими экспериментальным данным, а также заданного значения входной величины и соответствующего значения выходной величины.
3. Распечатанные результаты расчета по программе.
4. Вывод.
Лабораторная работа №2
Бланк результатов расчета
| Исходные данные | ||||||||||||
| Наименование фактора | Обозначение | Единицы измерения | Интервал варьирования | Уровень | ||||||||
| верхний | нулевой | нижний | ||||||||||
| +1 | -1 | |||||||||||
| 1. | x1 | |||||||||||
| 2. | x2 | |||||||||||
| Математическая модель (общий вид уравнения): | ||||||||||||
| Опыты | План | Параметр | Расчеты | |||||||||
| x0 | x1 | x2 | yu | 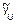 | 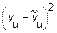 | |||||||
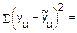 | ||||||||||||
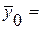 ; ; 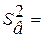 ; ; 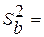 ; tт(fв = ; a = 0,05) = ; tт(fв = ; a = 0,05) = | ||||||||||||
| Коэффициенты уравнения регрессии | b0 | b1 | b2 | b12 | ||||||||
| Расчетное значение критерия Стьюдента tр | tр0 | tр1 | tр2 | tр12 | ||||||||
| Проверка значимости ("+" – значимый, "–" - незначимый) | ||||||||||||
 | ||||||||||||
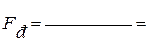 ; Fт(fад = ; fв = ; a = 0,05) = ; Fр Fт Математическая модель адекватно (неадекватно) описывает экспериментальные данные ; Fт(fад = ; fв = ; a = 0,05) = ; Fр Fт Математическая модель адекватно (неадекватно) описывает экспериментальные данные | ||||||||||||
| Полученное уравнение математической модели | ||||||||||||
| Кодир. переменные | ||||||||||||
| Натур. переменные | ||||||||||||
арианты индивидуальных заданий к лабораторной работе №2
(Номер варианта соответствует номеру студента в списке группы)
Вариант 1
На лабораторной молотковой дробилке был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета количества в измельченном угле фракции менее 3 мм (z=y, %) в зависимости от факторов: x1 - ширина щели решетки (b), мм; x2 - влажность измельчаемого угля (n), %. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 75,9 | |
| +1 | -1 | 84,15 | |
| -1 | +1 | 80,55 | |
| +1 | +1 | 78,45 | |
| 79,55 | |||
| 79,4 | |||
| 79,1 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 2
На лабораторной молотковой дробилке был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета количества в измельченном угле фракции менее 3 мм (z=y, %) в зависимости от факторов: x1 - ширина щели решетки (b), мм; x2 - частота вращения ротора (n), мин-1. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 52,85 | |
| +1 | -1 | 47,8 | |
| -1 | +1 | 63,25 | |
| +1 | +1 | 54,9 | |
| 55,9 | |||
| 54,7 | |||
| 53,4 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 3
На лабораторной молотковой дробилке был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета количества в измельченном угле фракции менее 3 мм (z=y, %) в зависимости от факторов: x1 - ширина щели решетки (b), мм; x2 - влажность измельчаемого угля (n), %. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 69,85 | |
| +1 | -1 | 65,2 | |
| -1 | +1 | 67,3 | |
| +1 | +1 | 62,15 | |
| 66,8 | |||
| 65,75 | |||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 4
На лабораторной молотковой дробилке был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета количества в измельченном угле фракции менее 3 мм (z=y, %) в зависимости от факторов: x1 - ширина щели решетки (b), мм; x2 - частота вращения ротора (n), мин-1. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 70,45 | |
| +1 | -1 | 78,3 | |
| -1 | +1 | 61,45 | |
| +1 | +1 | 56,6 | |
| 76,25 | |||
| 75,85 | |||
| 76,8 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 5
На лабораторной молотковой дробилке был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета количества в измельченном угле фракции менее 3 мм (z=y, %) в зависимости от факторов: x1 - ширина щели решетки (b), мм; x2 - влажность измельчаемого угля (n), %. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 62,2 | |
| +1 | -1 | 56,15 | |
| -1 | +1 | 54,2 | |
| +1 | +1 | 50,15 | |
| 52,3 | |||
| 52,15 | |||
| 51,65 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 6
На прокатной клети был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета интенсивности износа прокатных валков (Ио=y, мкм/об.) в зависимости от факторов: x1 - температура прокатываемого металла (Т), °С; x2 - абсолютное боковое обжатие (Dh), мм. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 0,024 | |
| +1 | -1 | 0,002 | |
| -1 | +1 | 0,08 | |
| +1 | +1 | 0,051 | |
| 0,037 | |||
| 0,042 | |||
| 0,039 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 7
На прокатной клети был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета интенсивности износа прокатных валков (Ио=y, мкм/об.) в зависимости от факторов: x1 - температура прокатываемого металла (Т), °С; x2 - скорость скольжения (Du), м/с. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 0,096 | |
| +1 | -1 | 0,005 | |
| -1 | +1 | 0,187 | |
| +1 | +1 | 0,115 | |
| 0,104 | |||
| 0,11 | |||
| 0,108 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | 0.9 | |
| Нижний уровень | 0.1 |
Вариант 8
На прокатной клети был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета интенсивности износа прокатных валков (Ио=y, мкм/об.) в зависимости от факторов: x1 - абсолютное боковое обжатие (Dh), мм; x2 - скорость скольжения (Du), м/с. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 0,186 | |
| +1 | -1 | 0,148 | |
| -1 | +1 | 0,386 | |
| +1 | +1 | 0,362 | |
| 0,283 | |||
| 0,274 | |||
| 0,278 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | 0.8 | |
| Нижний уровень | 0.2 |
Вариант 9
На прокатной клети был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета интенсивности износа прокатных валков (Ио=y, мкм/об.) в зависимости от факторов: x1 - температура прокатываемого металла (Т), °С; x2 - абсолютное боковое обжатие (Dh), мм. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 0,115 | |
| +1 | -1 | 0,075 | |
| -1 | +1 | 0,262 | |
| +1 | +1 | 0,224 | |
| 0,172 | |||
| 0,165 | |||
| 0,17 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 10
На прокатной клети был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета интенсивности износа прокатных валков (Ио=y, мкм/об.) в зависимости от факторов: x1 - абсолютное боковое обжатие (Dh), мм; x2 - скорость скольжения (Du), м/с. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | 0,013 | |
| +1 | -1 | 0,008 | |
| -1 | +1 | 0,12 | |
| +1 | +1 | 0,088 | |
| 0,05 | |||
| 0,042 | |||
| 0,048 |
| Уровни факторов | x1 | x2 |
| Верхний уровень | 0.9 | |
| Нижний уровень | 0.2 |
Вариант 11
В цехе был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета срока службы кладки печи (t=y, сут.) в зависимости от факторов: x1 - высота свода (H), м; x2 - длительность плавки (t), ч. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень | 3.0 |
Вариант 12
В цехе был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета срока службы кладки печи (t=y, сут.) в зависимости от факторов: x1 - площадь пламенного окна (S), м2; x2 - длительность плавки (t), ч. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 13
В цехе был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета срока службы кладки печи (t=y, сут.) в зависимости от факторов: x1 - высота свода (H), м; x2 - площадь пламенного окна (S), м2. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | 3.5 | |
| Нижний уровень | 3.2 |
Вариант 14
В цехе был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета срока службы кладки печи (t=y, сут.) в зависимости от факторов: x1 - высота свода (H), м; x2 - длительность плавки (t), ч. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | 3.2 | |
| Нижний уровень | 3.0 |
Вариант 15
В цехе был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета срока службы кладки печи (t=y, сут.) в зависимости от факторов: x1 - площадь пламенного окна (S), м2; x2 - длительность плавки (t), ч. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | 8.6 | |
| Нижний уровень | 9.5 |
Вариант 16
Для прутков диаметром 20 мм из стали Х18Н10Т, прокатываемых на стане 360, был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета предела текучести стали после прокатки и закалки (sт, МПа) в зависимости от факторов: x1 - температура металла перед началом прокатки (T), °С; x2 - число проходов (n). Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 17
Для прутков диаметром 20 мм из стали Х18Н10Т, прокатываемых на стане 360, был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета предела текучести стали после прокатки и закалки (sт, МПа) в зависимости от факторов: x1 - температура металла перед началом прокатки (T), °С; x2 - промежуток времени (пауза) между моментом окончания прокатки и закалкой (), с. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 18
Для прутков диаметром 20 мм из стали Х18Н10Т, прокатываемых на стане 360, был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета предела текучести стали после прокатки и закалки (sт, МПа) в зависимости от факторов: x1 - число проходов (n); x2 - промежуток времени (пауза) между моментом окончания прокатки и закалкой (), с. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 19
Для прутков диаметром 20 мм из стали Х18Н10Т, прокатываемых на стане 360, был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета предела текучести стали после прокатки и закалки (sт, МПа) в зависимости от факторов: x1 - температура металла перед началом прокатки (T), °С; x2 - число проходов (n). Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
Вариант 20
Для прутков диаметром 20 мм из стали Х18Н10Т, прокатываемых на стане 360, был проведен планированный эксперимент. Выполнить обработку результатов эксперимента и построить математическую модель для расчета предела текучести стали после прокатки и закалки (sт, МПа) в зависимости от факторов: x1 - температура металла перед началом прокатки (T), °С; x2 - промежуток времени (пауза) между моментом окончания прокатки и закалкой (), с. Представить уравнение математической модели в кодированных и натуральных переменных.
Матрица планирования и результаты эксперимента
| Номер опыта | x1 | x2 | y |
| -1 | -1 | ||
| +1 | -1 | ||
| -1 | +1 | ||
| +1 | +1 | ||
| Уровни факторов | x1 | x2 |
| Верхний уровень | ||
| Нижний уровень |
