Виды (типы) линий тренда

Арифметическая (линейная)

Линейная аппроксимация — это прямая линия, наилучшим образом описывающая набор данных. Она применяется в самых простых случаях, когда точки данных расположены близко к прямой. Говоря другими словами, линейная аппроксимация хороша для величины, которая увеличивается или убывает с постоянной скоростью.

Формула:

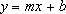
где m - угол наклона и b - координата пересечения оси абсцисс.

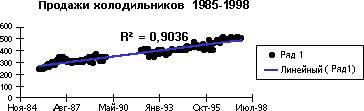
В приведенном ниже примере линейное приближение показывает равномерное увеличение объема продаж холодильников в течение 13 лет. Следует заметить, что значение R-квадрат в данном случае составляет 0,9036. Это свидетельствует о достаточно хорошем согласовании линии аппроксимации с фактическими данными.

Логарифмическая

Логарифмическая аппроксимация хорошо описывает величину, которая вначале быстро растет или убывает, а затем постепенно стабилизируется. Описывает как положительные, так и отрицательные величины.

Формула:

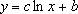
где c и b - константы, ln - функция натурального логарифма.

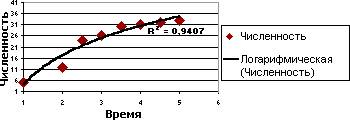
Приведенный ниже пример использует логарифмическое приближение для иллюстрации прогнозируемого роста популяции животных на ограниченной территории. По мере того как свободного пространства становится все меньше, темпы роста популяции также снижаются. Следует заметить, что значение R-квадрат в данном примере равно 0,9407; это указывает на то, что аппроксимирующая кривая описывает данные с достаточно высокой степенью достоверности.

Полиномиальная

Полиномиальная аппроксимация используется для описания величин, попеременно возрастающих и убывающих. Она полезна, например, для анализа большого набора данных о нестабильной величине. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум. Полином третьей степени имеет один или два экстремума. Полином четвертой степени может иметь не более трех экстремумов.

Формула:

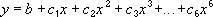
где b и 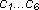— константы.

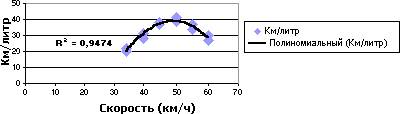
Ниже на примере аппроксимации полиномом второго порядка (одна вершина) показана зависимость скорости от потребления топлива. Следует заметить, что значение R-квадрат в данном случае составляет 0,9474. Это достаточно хорошо согласуется с фактическими данными.

Степенная

Степенное приближение дает хорошие результаты, если зависимость, которая содержится в данных, характеризуется постоянной скоростью роста. Примером такой зависимости может служить график ускорения автомобиля. Если в данных имеются нулевые или отрицательные значения, использование степенного приближения невозможно.

Формула:

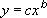
где c и b - константы.

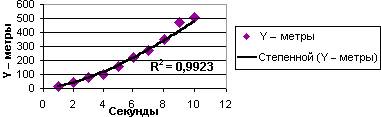
Ниже показан пример зависимости пройденного расстояния от времени (в секундах). По степенной линии тренда ясно видно увеличение ускорения. Обратите внимание, что значение R-квадрат в данном примере равно 0,9923. Это говорит о высокой точности используемого приближения.

Экспоненциальная

Экспоненциальное приближение следует использовать в том случае, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, этот вид приближения неприменим.

Формула:

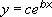
где c и b - константы, e - основание натурального логарифма.

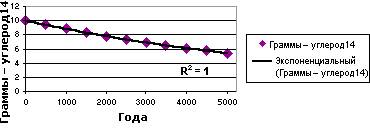
На приведенном ниже на примере экспоненциальное приближение иллюстрирует процесс распада углерода 14. Следует заметить, что значение R-квадрат здесь равно 1, то есть линия приближения идеально соответствует данным.