Нахождение компонент двусвязности (блоков) графа

Если в связном графе найдутся две вершины u₁ и u₂ такие, что любой путь между ними будет проходить через вершину v, то вершина v будет называться точкой сочленения.

Можно дать эквивалентное определение точки сочленения.

Вершина v графа G=<V, E> называется точкой сочленения, если удаление этой вершины и всех выходящих из нее ребер, ведет к увеличению компонент связности графа.

Если в связном (состоящем из одной компоненты связности) графе нет точек сочленения, он – двусвязный.

Любой максимальный двусвязный подграф графа G называется компонентой двусвязностиили блоком этого графа (рис. 8.17).

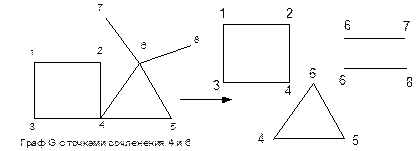
Рис. 8.17. Блоки графа G

Вопрос 1. Что будет являться пересечением двух различных блоков графа?

Вопрос 2. Что произойдет с блоком, если к нему присоединить ребро графа, имеющего с блоком общую точку и не принадлежащего блоку?

Двусвязность графа – очень полезное свойство для некоторых прикладных задач.

Представим себе, что вершины графа – телеграфные станции; ребра – линии передач. Пусть одна из станций вышла из строя. Если граф двусвязный, то между любыми двумя оставшимися станциями сохранится связь.

Для многих задач важно знать блоки графа. Например, находить все элементарные циклы графа G можно отдельно для каждого блока графа G.

Нахождение точек сочленения и блоков графа – классическая задача. Будем искать точки сочленения, обходя все вершины графа методом поиска в глубину. Будем не только обходить вершины графа, но и строить его каркас.

При построении каркаса поиском в глубину для двух вершин u и v, связанных ребром, всегда точно известно: или u – потомок v, или наоборот. Как распознать точку сочленения s, если уже построен каркас D графа G?

Вот критерий точки сочленения:

– или это корень, имеющий не менее двух сыновей в D;

– или у вершины s есть хотя бы один сын u такой, что ни он, ни его потомки не связаны хордами с предками s.

Рассмотрим рис. 8.18. Номера вершин – номера, которые получают вершины графа во время построения каркаса. Покажем, что вершина s удовлетворяет второму условию критерия.

По построению каркаса s имеет сына 3 и потомка 4. Предок s – вершина k. Сын 3 и его потомок 4 не связаны хордами с k. Итак, s – точка сочленения и граф G имеет первый блок = {s–3, 3–4, s–4}.

Рис. 8.18. Точки сочленения

Вопрос 3. С какой вершиной нужно соединить вершину 4, чтобы граф G стал двусвязным?

Вершина k – точка сочленения, так как она корень, имеющая двух сыновей: s и 5. Поэтому граф G имеет второй блок = {k–s} и третий блок = {k–5}.

Зная критерий точки сочленения, опишем алгоритм нахождения этих точек.

Пусть алгоритм поиска в глубину строит каркас D графа G. Для каждой вершины v будем вычислять два значения: GLN[v] и MIN[v].

GLN[v] – просто номер, который получает вершина при построении каркаса. Например, для корня GLN[k]=1.

Пусть вершина v соединена хордами (вспомните, что такое хорды для каркаса D) c какими-то вершинами X₁, …, X_k. Выберем минимальный из номеров этих вершин:

X[v] = min {GLN[X₁], …, GLN[X_k]}.

Вопрос 4. Какие вершины графа на рис. 8.18 соединены хордами с вершиной s?

Пусть w – любой потомок вершины v. Он также может быть связан хордами с какими-то вершинами Y₁, …, Y_р.

Подсчитаем Y[w] = min {GLN [Y₁], …, GLN [Y_р]}.

И, наконец, подсчитаем Y[w] для каждого w – потомка v и выберем из них минимальный.

Y[v] = min {Y[w], w – любой потомок v}

Минимальный из трех номеров {GLN[v], X[v], Y[v]} назовем MIN[v]:

MIN [v]= min {GLN[v], X[v], Y[v]}.

MIN[v] легко вычислить по индукции.

Пусть для всех сыновей U₁, …, U_k вершины v MIN[U₁], …, MIN[U_k] уже вычислены.

Тогда MIN[v] = min {GLN[v], X[v], MIN[u]},

где MIN[u]= min {MIN[U₁], …, MIN[U_k]}.

Вспомним критерий точки сочленения. Это либо корень с двумя сыновьями, либо предки этой точки и потомки хотя бы одного сына не соединены хордами.

Запишем этот критерий через GLN и MIN.

МIN[u] – минимальный из номеров вершин, с которыми соединен сын u и его потомки. Если среди этих вершин не будет предков v, то критерий выполнится. Номера предков строго меньше GLN[v], поэтому MIN[u] ³ GLN [v] для некоторого сына u вершины v.

Вопрос 5. Вычислите MIN[3] для сына 3 вершины s. Выполнится ли для s критерий?

АЛГОРИТМ {Нахождение компонент двусвязности графа}

Данные: Граф G=<V, Е> без изолированных вершин, представленный списками инцидентности ЗАПИСЬ[v], v Î V.

Результаты: Множество ребер всех компонент двусвязности. Переменные MIN, GLN, CTEK, num – глобальные.

1 procedure BLOC(v,p);

{Поиск в глубину, начиная с v.

В стек записывают ся ребра блоков, p – отец v}

2 begin

3 num:= num+1; GLN[v]:= num; {нумеруем v}

4 MIN[v]:= GLN[v];

5 for u Є ЗАПИСЬ[v] do

6 if GLN[u]=0 then {u – новая, (v-u) – ветвь}

7 begin

8 СТЕК <= (v-u);{Ветвь поместили в стек, поиск
продолжается с u}

9 BLOC(u, v) {у u не осталось новых соседей,
был подсчитан MIN[u]. Пора
пересчитать MIN[v] и проверить
критерий}

10 MIN[v]:= min(MIN[v], MIN[u]);

11 if MIN[u]>=GLN[v] then

{v – точка сочленения. Ребра, занесенные в
стек последними до (v–u) включительно –
блок, связывающий u всех его потомков}

12 begin {печать ребер блока}

13 repeat

14 e <= СТЕК;

15 write(e);

16 until e=(v-u);

17 write(;) {знак конца блока}

18 end

19 end {if GLN[u]=0}

20 else {u – не новая}

21 if (u<>p) and (GLN[u]<GLN[v]) then

22 begin {условие хорды}

23 СТЕК <= (v-u);{v соединена хордой с u,

пересчитаем MIN[v]}

24 MIN[v]:= min(MIN[v], GLN[u])

25 end

26 end;

1 begin {основная программа}

2 for v Î V do

3 begin

4 GLN[v]:= 0; MIN[v]:= n

5 end;

6 СТЕК:= NIL; num:= 0;

7 BLOC(k,0);

8 end.

Алгоритм составлен. Осталось доказать его корректность.

Покажем, что вызов BLOC(v, 0) для любой вершины v графа приведет к печати всех блоков этого графа.

1. Если граф двусвязный, то он состоит из одного блока и не имеет точек сочленения. В строке 8 в стек будут заноситься все ветви каркаса, в строке 23 – хорды. Точек сочленения нет, поэтому критерий 11 выполнится первый раз для корня. К корню мы вернемся, рассмотрев все вершины и заслав в стек все ребра.

2. Пусть граф содержит i (i>1) блоков, а алгоритм исправно работает для любого графа, содержащего блоков не более i-1.

Начинаем поиск в глубину и на каком-то шаге первый раз встретим ребро (v–u) такое, что MIN[u] ³ GLN[v] (критерий). Вершина v – корень или точка сочленения, u – сын вершины v. Так как проверка критерия выполнилась первый раз, то все потомки u рассмотрены и точек сочленения среди них нет. Следовательно, верхняя часть стека вплоть до ребра (v–u) – первый блок. Удалим этот блок, оставив только вершину v.

Запустим алгоритм для оставшегося графа. Единственным изменением в его работе будет следующее: когда v будет просмотрена первый раз, цикл 5 не будет перебирать вершины из удаленного блока.

В графе осталось i-1 блоков, и по индуктивному предположению они будут найдены, а доказательство – окончено.

Оценим вычислительную сложность алгоритма.

Цикл 2 требует для n вершин О(n) шагов. Вызов BLOC(v, 0) повлечет О(n+m) шагов, где n и m – число вершин и ребер, так как столько требует поиск в глубину. Каждое ребро в цикле 13 удаляется из стека и выводится на печать ровно один раз, т.е. не более О(m) шагов. Сумма всех этих слагаемых не превосходит О(n+m) шагов.

Ответ 1. Точка сочленения или ничего.

Ответ 2. Максимальность блока означает, что, присоединяя к нему любой подграф, мы автоматически присоединяем точку сочленения.

Ответ 3. С вершиной 5.

Ответ 4. Вершина 4.

Ответ 5.MIN[3]=2, так как потомок 3 вершина 4 связана хордой с s, а GLN[s]=2. GLN[s]=MIN[3] и критерий выполнен.

Эйлеровы пути

Эйлеровым путемв графе называется произвольный путь, проходящий через каждое ребро в точности один раз.

Если путь заканчивается в начальной вершине, то он называется эйлеровым циклом(рис. 8.19).

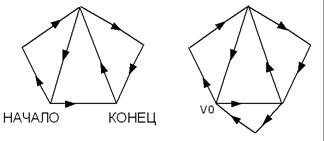
Рис. 8.19. Эйлеров цикл, эйлеров путь

Задача существования эйлерова пути в заданном графе была решена великим русским математиком Леонардом Эйлером в 1736 году.

Представленное им необходимое и достаточное условие существования такого пути считается первой в истории математики теоремой теории графов.

ТЕОРЕМА

Эйлеров путь существует тогда и только тогда, когда граф связный и содержит не более двух вершин нечетной степени. (Напомним, степень вершины – число смежных с нею ребер).

Заметим, что число вершин нечетной степени в любом графе всегда четно. Это легко доказать.

Просуммируем степени всех вершин графа. Эта сумма равна
2m – удвоенному числу ребер, так как каждое ребро соединяет две вершины. Вклад в эту сумму вершин четной степени – четен, поэтому вклад вершин нечетной степени тоже должен быть четен. Для этого их должно быть четное количество (нечетное число ребер ´ четное число вершин = четный результат).

Новая формулировка теоремы: