Метод подведения под знак дифференциала для простейших дробей
Переходим к рассмотрению следующего типа дробей:
, 
, 
, 
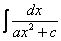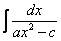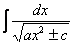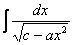(коэффициенты a и c не равны нулю).
На самом деле пара случаев с арксинусом и арктангенсом уже проскальзывала на уроке Метод замены переменной в неопределенном интеграле. Решаются такие примеры способом подведения функции под знак дифференциала и дальнейшим интегрированием с помощью таблицы. Вот еще типовые примеры с длинным и высоким логарифмом:
Пример 5
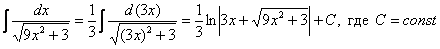
Пример 6
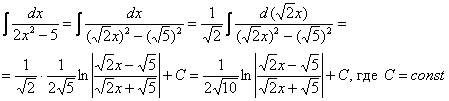
Тут целесообразно взять в руки таблицу интегралов и проследить, по каким формулам и какосуществляется превращение. Обратите внимание, как и зачемвыделяются квадраты в данных примерах. В частности, в Примере 6 сначала необходимо представить знаменатель (2x2-5) в виде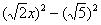 
, а потом подвести 
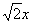под знак дифференциала. А сделать это всё нужно для того, чтобы воспользоваться стандартной табличной формулой 
.
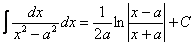Попробуйте самостоятельно решить примеры №№ 7 и 8, тем более, что они достаточно короткие.
Пример 7
Найти неопределенный интеграл:
.
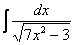Пример 8
Найти неопределенный интеграл:
.
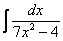Если Вам удастся выполнить еще и проверку данных примеров, то Ваши навыки дифференцирования на высоте.
Метод выделения полного квадрата
Интегралы вида
, 
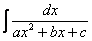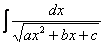
(коэффициенты a и b не равны нулю) решаются методом выделения полного квадрата.
На самом деле такие интегралы сводятся к одному из четырех табличных интегралов, которые мы только что рассмотрели. А достигается это с помощью знакомых формул сокращенного умножения:
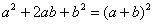или 
.
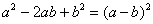Формулы применяются именно в таком направлении, то есть идея метода состоит в том, чтобы в знаменателе искусственно организовать выражения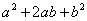 
либо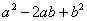 
, а затем преобразовать их, соответственно, в 
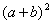либо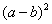 
.
Пример 9
Найти неопределенный интеграл
.
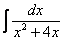Это простейший пример, в котором при слагаемомx2– единичный коэффициент(а не какое-нибудь число или минус).
Смотрим на знаменатель, здесь всё дело явно сведется к случаю 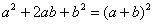. Начинаем преобразование знаменателя:
.
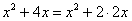Очевидно, что нужно прибавлять 4. И, чтобы выражение не изменилось – эту же четверку и вычитать:
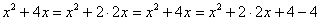
Теперь можно применить формулу :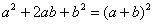
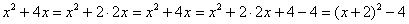
После того, как преобразование закончено ВСЕГДАжелательно выполнить обратный ход: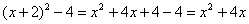 
, всё нормально, ошибок нет.
Чистовое оформление рассматриваемого примера должно выглядеть примерно так:
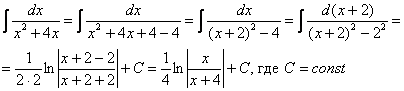
Пример 10
Найти неопределенный интеграл
.
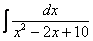Это пример для самостоятельного решения, ответ в конце урока
Пример 11
Найти неопределенный интеграл
.
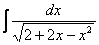Что делать, когда перед x2 находится минус? В этом случае нужно вынести минус за скобки и расположить слагаемые в нужном нам порядке: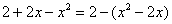 
. Константу(«двойку» в данном случае) не трогаем!
Теперь в скобках прибавляем единичку. Анализируя выражение, приходим к выводу, что и за скобкой нужно единичку прибавить:
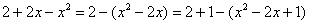
Тут получилась формула 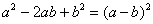, применяем:
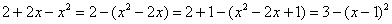
ВСЕГДА выполняем на черновике проверку:
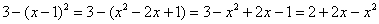
что и требовалось проверить.
Чистовое оформление примера выглядит примерно так:
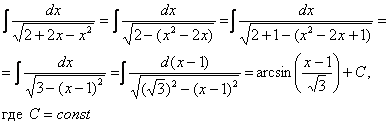
Усложняем задачу.
Пример 12
Найти неопределенный интеграл:
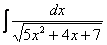
Здесь при слагаемом x2 уже не единичный коэффициент, а «пятёрка».
(1) Если при x2 находится константа, то её сразу выносим за скобки.
(2) И вообще эту константу всегда лучше вынести за пределы интеграла, чтобы она не мешалась под ногами.
(3) Очевидно, что всё сводится к формуле .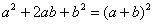
Надо разобраться в слагаемом 2ab, а точнее, найти величину b получить «двойку».
(4) Как видим, здесь b = (2/5). Значит, к выражению прибавляем (2/5)2 = (4/25), и эту же дробь вычитаем.
(5) Теперь выделяем полный квадрат. В общем случае также надо вычислить (7/5)-(4/25), но здесь у нас вырисовывается формула длинного логарифма
,
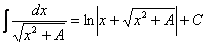и действие (7/5)-(4/25) выполнять не имеет смысла, почему – станет ясно чуть ниже.
(6) Собственно, можно применить формулу ,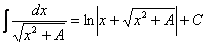
только вместо «икс» у нас x+(2/5), что не отменяет справедливость табличного интеграла. Строго говоря, пропущен один шаг – перед интегрированием функцию x+(2/5) следовало подвести под знак дифференциала:
,
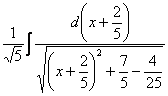но, как уже неоднократно отмечалось, этим часто пренебрегают.
(7) В ответе под корнем желательно раскрыть все скобки обратно:
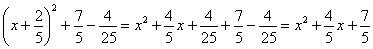
Пример 13
Найти неопределенный интеграл
.
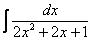Это пример для самостоятельного решения. Ответ в конце урока.
Существуют интегралы с корнями в знаменателе, которые с помощью замены сводятся к интегралам рассмотренного типа, о них можно прочитать в статье Сложные интегралы, но она рассчитана на весьма подготовленных студентов.