Вопрос 49. Полигон и гистограмма. Эмпирическая функция распределения

Пусть известно статистическое распределение частот количественного признака Х. Обозначим: 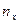- число наблюдений, при которых наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем выборки). Ясно, что относительная частота события Х<x равна 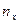/n. Если х меняется, то меняется и относительная частота, т.е относительная частота 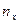/n есть функция от х. Так как эта функция находится опытным путем, то ее называют эмпирической. Эмпирическая функция – это функция 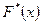, определяющая для каждого значения х относительную частоту события Х<х , т.е 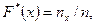где n-объем выборки, 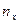- число вариант меньших х. Таким образом, чтобы найти например 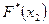, надо число вариант, меньших 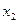, разделить на объем выборки: 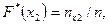В отличие от эмпирической функции распределения выборки функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция определяет вероятность события, а эмпирическая определяет относительную частоту этого же события. Теоретическая и эмпирическая функции обладают общими свойствами. 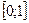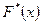Свойства эмпирической функции:1) значения эмпирической функции принадлежат отрезку ; 2) - неубывающая функция; 3) если 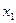- наименьшая варианта, то 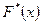=0 при 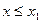; если 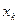- наибольшая варианта, то 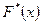=1 при 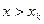. Таким образом, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму. Полигон частот – ломаная, отрезки которой соединяют точки 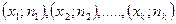. Для построения полигона частот на оси абсцисс откладывают варианты 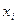, а на оси ординат – соответствующие им частоты 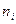. Точки соединяют отрезками прямых и получают полигон частот. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 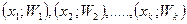. Для построения полигона относительных частот на оси Х откладывают варианты 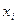, а на оси Y – соответствующие им относительные частоты W_i. Точки соединяют отрезками прямых и получают полигон относительных частот. В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько различных частичных интервалов длиной h и находят для каждого частичного интервала 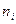- сумму частот вариант, попавших в i-й интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты которых равны отношению 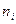/h (плотность частоты). Для построения гистограммы частот по оси Х откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси Х на расстоянии 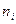/h.