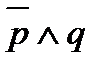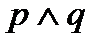Теория алгебры множеств
Множество – совокупность каких-либо объектов, обладающих некоторым общим признаком. Обозначаются заглавными буквами латинского алфавита A,B,C,X1,X2…
Множества состоят из элементов, которые обозначаются малыми буквами латинского алфавита a,c,d,y1,y2. Если элемент входит в данное множество, то он принадлежит этому множеству 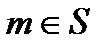 . Подмножество - это любая часть данного множества, выбранная по определенному признаку. Каждый элемент подмножества является элементом данного множества. Если множество является подмножеством другого множества, то говорят, что оно включено в это множество
. Подмножество - это любая часть данного множества, выбранная по определенному признаку. Каждый элемент подмножества является элементом данного множества. Если множество является подмножеством другого множества, то говорят, что оно включено в это множество 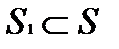 .
.
В зависимости от числа входящих во множество элементов, множества можно классифицировать по объему: конечные, бесконечные и пустые множества. Число элементов конечного множества называется мощностью множества.
Над множествами можно производить следующие операции:
1. Сумма (объединение )- это новое множество, элементы которого принадлежат (обладают свойствами) хотя бы одному из множеств А или В.
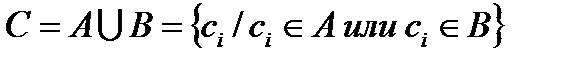
2. Произведение (пересечение)- это новое множество, элементы которого принадлежат (обладают свойствами) и множеству А и множеству В.
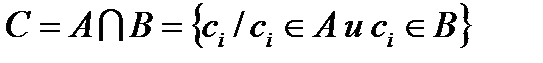
3. Вычитание (разность)- это новое множество, элементы которого принадлежат (обладают свойствами) множеству А и не принадлежат множеству В.
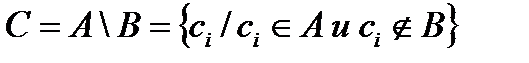
4. Дополнение (до универсального множества) – это новое множество, элементы которого не принадлежат множеству А, но принадлежат универсальному множеству.
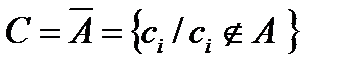
Все свойства, законы и формулы соответствующие алгебре логики выполняются и для теории множеств. Основные операции теории множеств (пересечение, объединение и дополнение) соответствуют основным операциям теории логики (конъюнкции, дизъюнкции и инверсии), поэтому при доказательстве равносильности множеств или упрощении можно заменять операции множеств на логические действия. Законы и свойства можно проверить графически. Графическое изображение множеств с помощью графических объектов называется построением множеств с помощью теоретико-множественных диаграмм или диаграмм Эйлера-Венна. Основные операции теории множеств можно графически изобразить так:
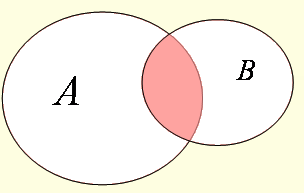 | 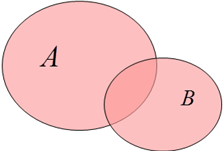 | 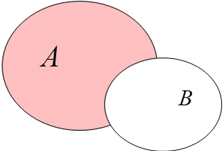 | 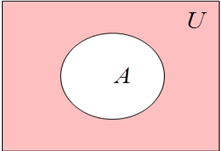 |
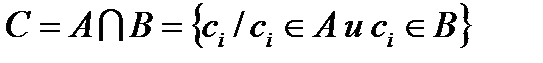 | 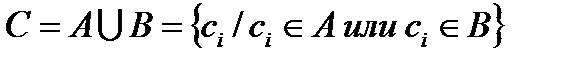 | 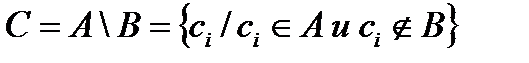 | 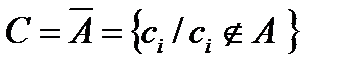 |
Задание.
Заданы множества А={0,1,2,3,6,7}; В={2,6,8}, С={7,8}.
Осуществить следующие операции над множествами:
В∩С; ВUС; А\В; (А∩С)\В.
Решение:
Используя определения операций над множествами, найдем элементы полученных множеств после осуществления операций над ними:
1 В∩С = {2,6,8}∩{7,8} = {8} –элемент, принадлежащий одновременно обоим множествам.
2 ВUС = {2,6,8}U{7,8} = {2,6,7,8} – элементы, принадлежащие хотя бы одному из множеств.
3 А\В = {0,1,2,3,6,7} \{2,6,8} = {0,1,3,7} – элементы, которые входят во множество А, но не принадлежат множеству В.
4 (А∩С)\В = ({0,1,2,3,6,7}∩{7,8})\{2,6,8} = {7}\{2,6,8} = {7} - выполняем действие сначала в скобках, умножаем множества А и С, результатом будет один общий элемент 7, затем из полученного действия вычитаем множество В, так как в нем нет таких элементов, то при вычитании оно не меняется.
Построим теоретико-множественные диаграммы множеств А, В, С, выделив осуществленные операции:
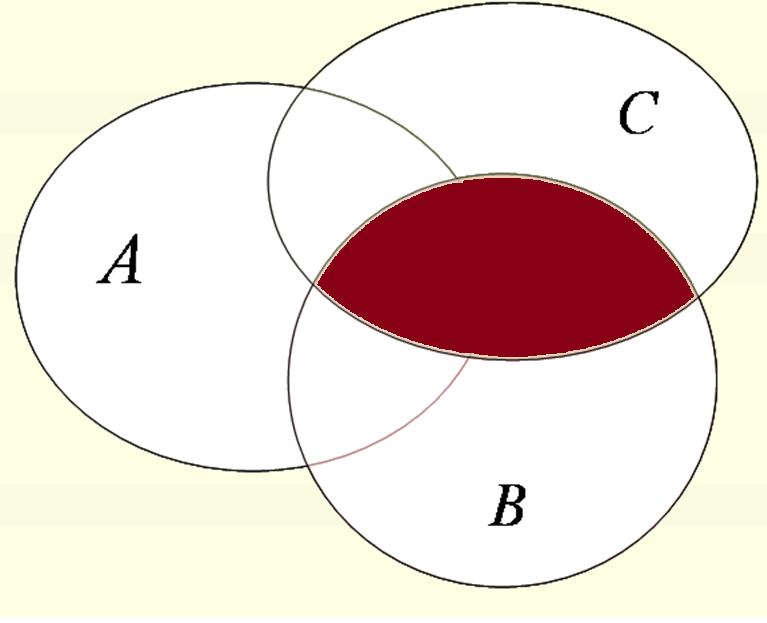 | В∩С | 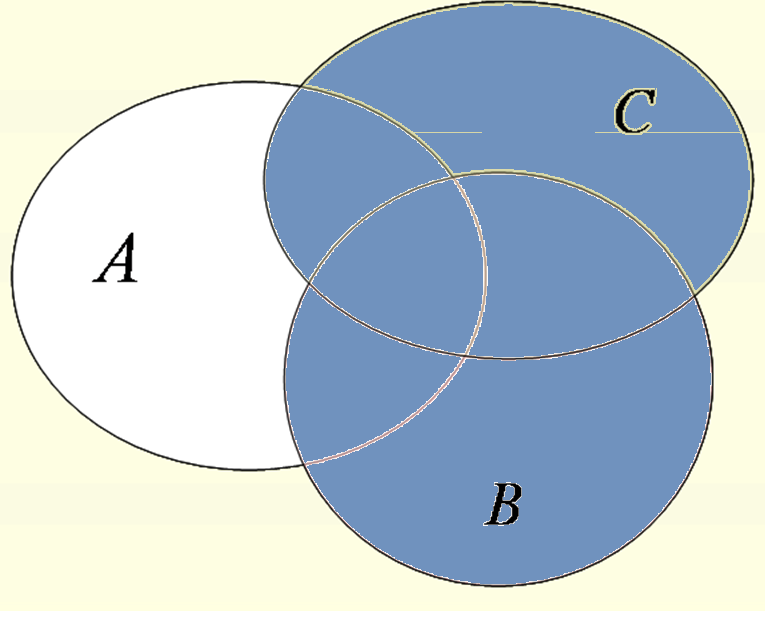 | ВUС | ||
| А\В | 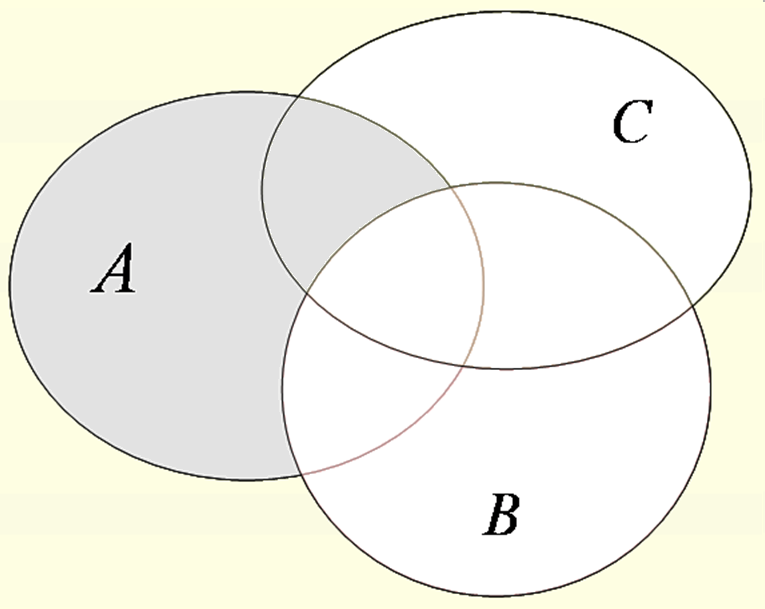 | (А∩С)\В | 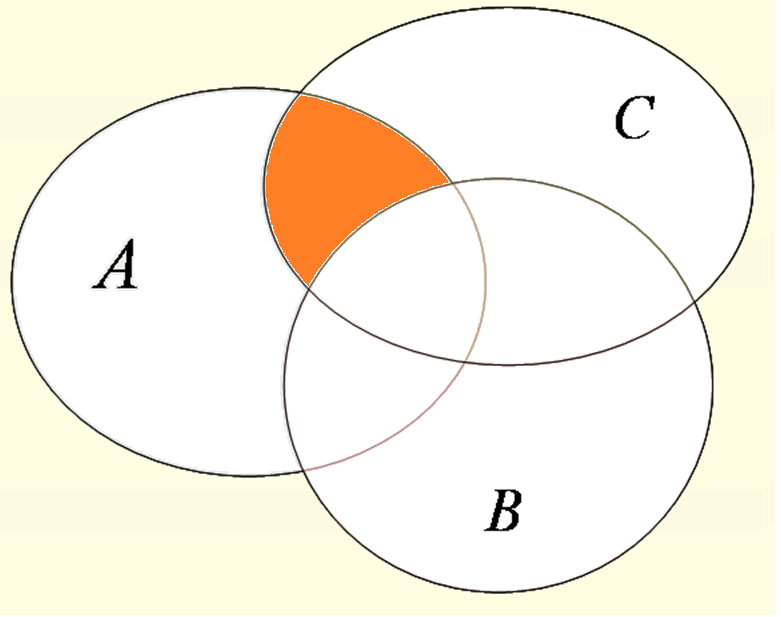 | ||
Булевы функции
Рассмотрим соответствие между двумя множествами. Если каждому набору, состоящему из n-элементов (нулей и единиц) поставим в соответствие 0 или 1, то получим функцию называющуюся булевой.
Функцию A (a1, a2…an), принимающую одной из двух значений 0 или 1, от n переменных, каждая из которых принимает одно из двух значений 0 или 1, будет называть булевой функцией A (a1, a2…an) от n переменных
f: 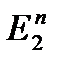
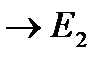 , где
, где 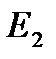 = {0,1}
= {0,1}
функция алгебры логики (булева функция)
Две булевы функции называются равными, если для любых одинаковых наборов значений аргументов обе функции принимают одинаковые значения.
Булеву функцию от n переменных можно задать таблицей истинности. Для того, чтобы рассмотреть всевозможные варианты булевых функций для n переменных необходимо составить 2n различных комбинаций их значений, поэтому количество вариантов булевых функций для n переменных будет 22n. Рассмотрим варианты булевых функции для двух переменных и опишем их тип:
| x | Тип булевой функции | |||||
| y | ||||||
| f1 | константа 0 (тождественно-истинная функция) | |||||
| f2 | x × y | конъюнкция переменных x, y | ||||
| f3 | ||||||
| f4 | x | |||||
| f5 | ||||||
| f6 | y | |||||
| f7 | x + y | отрицание эквивалентности | ||||
| f8 | x Ú y | дизъюнкция переменных x, y | ||||
| f9 | x ¯ y | отрицание дизъюнкции | ||||
| f10 | x <=> y | эквивалентность | ||||
| f11 | y¢ | отрицание переменной y | ||||
| f12 | y =>x | импликация переменных y, x | ||||
| f13 | x¢ | отрицание переменной x | ||||
| f14 | x =>y | импликация | ||||
| f15 | x | y | отрицание конъюнкции | ||||
| f16 | константа 1 (тождественно-ложная функция) |
Любую булеву функцию можно записать в виде формулы алгебры высказывания и наоборот. Все свойства, законы и формулы соответствующие теории алгебры логики соответствуют и теории булевых функций.
Если некоторая функция f(x1, x2, ..,xn) заданасвоей таблицей истинности, томожнопостроить множество равнозначных формул, которые будут принимать одинаковые значения функции на всех наборах переменных. Для того, чтобы эту проблему решить нам необходимо познакомиться с такими формами записи функций, которые дадут однозначную запись формулы булевой функции, используя таблицу истинности. Такие формы называются совершенными.
Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных произведений, называется дизъюнктивной нормальной формой (ДНФ) данной формулы.
Например,
| элементарные произведения |
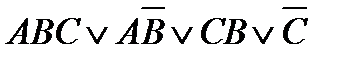 - ДНФ
- ДНФ Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных сумм (дизъюнктивных одночленов), называется конъюнктивной нормальной формой (КНФ) данной формулы
Например,
| элементарные суммы |
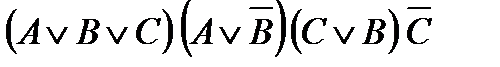 - КНФ
- КНФ Для того, чтобы любую булеву функцию представить в виде дизъюнктивной или конъюнктивной нормальной формы достаточно выполнить ряд равносильных преобразований, используя свойства, законы и формулы алгебры логики. Перечислим правила, которых нужно придерживаться при переводе булевых функций в ДНФ и КНФ:
1.
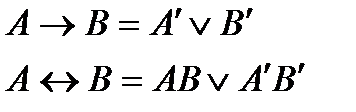 |
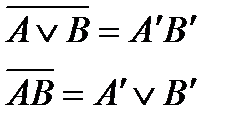 |
2.Заменить знак отрицания, относящийся к выражению, знаками отрицания, относящимися к отдельным переменным.
3.
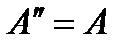 |
4.Применить, если нужно свойства, законы, формулы алгебры логики
Задание.
Привести заданную булеву функцию к ее нормальным формам,
используя равносильные преобразования:
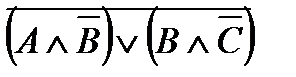
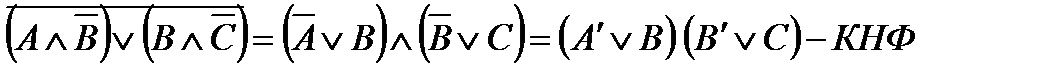
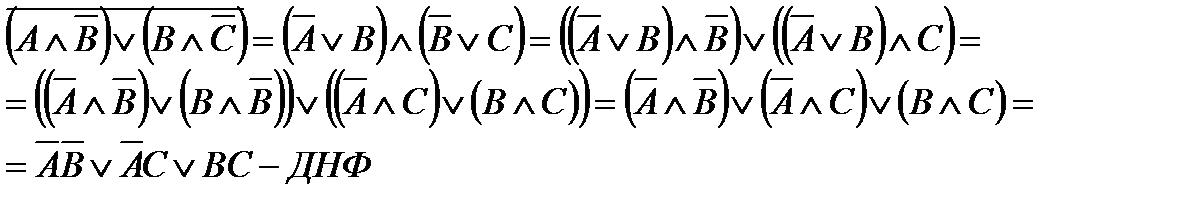
В ходе преобразовании использовали:
1) закон инверсии (избавились от знака отрицания над выражением)
2) распределительный закон (перемножили скобку на скобку)
3) свойство конъюнкции (умножение на свое отрицание)
4) свойство дизъюнкции (сложение с нулем)
Совершенной дизъюнктивной (конъюнктивной) нормальной формой (СДНФ, СКНФ) называется ее ДНФ (КНФ), обладающая следующими свойствами:
1. ДНФ (КНФ) не содержит двух одинаковых слагаемых (множителей)
2. Ни одно слагаемое (сомножитель) не содержит одновременно двух одинаковых сомножителей (слагаемых)
3. Ни одно слагаемое (сомножитель) не содержит одновременно некоторое высказывание и его отрицание
4. Каждое слагаемое (сомножитель) содержит в качестве сомножителя (слагаемого) либо само высказывание, либо его отрицание для всех переменных, входящих в формулу
В выполненном выше задании, найденные формы булевой функции не будут являться совершенными, так как все элементарные суммы (произведения) в данной функции должны содержать переменные А, В, С или их отрицания. Для приведения булевой функции к совершенным формам можно воспользоваться таблицей истинности. Для этого используем следующее правило:
СДНФ содержит столько слагаемых, сколько единиц имеет таблица истинности. Эти единицы соответствуют тем наборам переменных, при которых каждое слагаемое (элементарная конъюнкция) обращается в единицу, т.е. переменным, входящим без знака отрицания соответствует 1, а со знаком отрицания – 0
СКНФ содержит столько сомножителей, сколько нулей имеет таблица истинности. Эти нули соответствуют тем наборам переменных, при которых каждый сомножитель (элементарная сумма) обращается в нуль, т.е. переменным, входящим в элементарную сумму без знака отрицания соответствует 0, а со знаком отрицания – 1
Задание.
Привести заданную булеву функцию к ее совершенным нормальным формам, используя таблицу истинности:
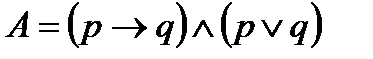
1. Строим для заданной функции таблицу истинности
|
2. Отметим строки, где значение функции равно 1 (СДНФ содержит два слагаемых)
3. Составляем для этих строк элементарные произведения: в первом произведении значения переменных p=0, q=1, поэтому 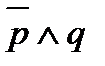 ; во втором произведении значения переменных p=1, q=1, поэтому
; во втором произведении значения переменных p=1, q=1, поэтому 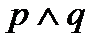
4. Отметим строки, где значение функции равно 0 (СКНФ содержит два сомножителя)
5. Составляем для этих строк элементарные суммы: в первой сумме значения переменных p=0, q=0, поэтому 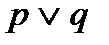 ; во второй сумме значения переменных p=1, q=0, поэтому
; во второй сумме значения переменных p=1, q=0, поэтому 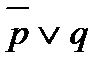
6. Записываем заданную функцию в совершенной дизъюнктивной форме (дизъюнкция элементарных произведений):
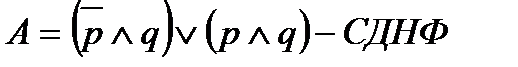
7. Записываем заданную функцию в совершенной конъюнктивной форме (конъюнкция элементарных сумм):
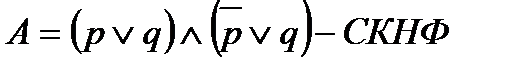
Каждая формула алгебры логики (булева функция) имеет единственную СДНФ (СКНФ)
Тоджественно-ложная формула не имеет СДНФ
Тождественно-истинная формула не имеет СКНФ
Основные понятия и законы математической логики очень тесным образом связана с вопросами конструирования и программирования ВТ. Алгебра логики нашла широкое применение при разработке релейно-контактных схем. С помощью формул алгебры логики можно описать любую релейно-контактную схему, упростить, привести к равносильной схеме. Так как любая схема содержит только два возможных соединения контактов (если контакт замкнут – 1, если разомкнут -0): параллельное и последовательное, то составив таблицу зависимости состояния цепи от всевозможных комбинаций состояния контактов, получим:
Цепь с последовательным соединением соответствует логической операции конъюнкция, т.к. ток в цепи появляется только при одновременном замыкании контактов А и В. Цепь с параллельным соединением соответствует логической операции дизъюнкция, т.к. ток в цепи появляется как при замыкании одного из контактов А или В, так и при одновременном их замыкании.
Задание.
Построить релейно-контактные схемы для F(а, в, с), если известны некоторые значения, а остальные значения функции F равны нулю. Упростить схему, если это возможно:
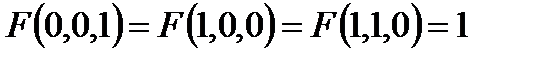
Решение:
1 Используя приведенные значения функции, построим таблицу истинности и по ней зададим формулу (в виде любой совершенной формы) заданной функции:
| а | в | с | F | элементарные произведения |
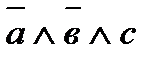 | ||||
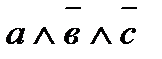 | ||||
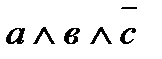 | ||||
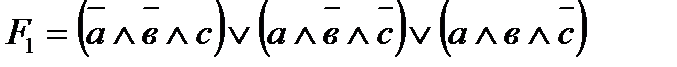
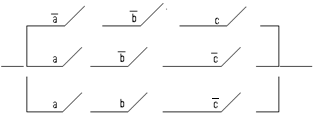
2 Строим релейно-контактную схему, где элементарные произведения – это последовательные соединения контактов, а их дизъюнкция – это их объединение в параллельные соединения:
3 Для упрощения релейно-контактной схемы, минимизируем соответствующую ей формулу. Проводим цепочку равносильных преобразований, пока формула не станет минимальной:
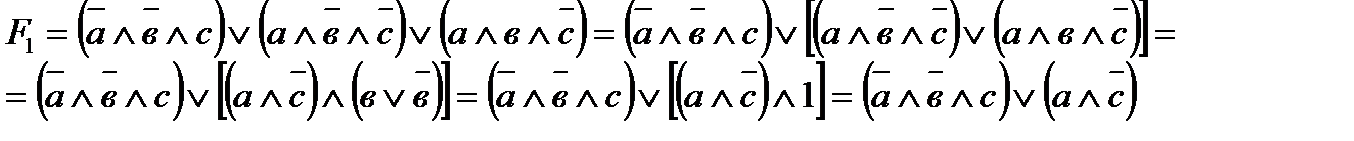
В ходе преобразовании использовали:
1) сочетательный закон (объединение второго и третьего слагаемого)
2) распределительный закон (вынесли общий множитель за скобку)
3) свойство дизъюнкции (закон исключения третьего)
4) свойство конъюнкции (умножение на единицу)
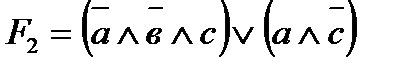
4 Строим упрощенную релейно-контактную схему:
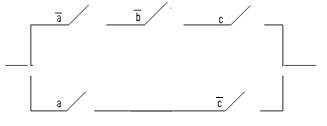
5 Делаем проверку равносильности двух полученных функций F1 и F2, используя таблицу истинности:
| а | в | с | F1 |  | 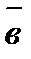 | 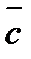 | 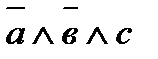 | 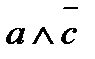 | F2 |
Так как значения функций F1 и F2 совпадают на всех наборах переменных, то они являются равнозначными. Делаем вывод, что нарисованные схемы являются равносильными друг другу и заданной функции F(а, в, с).
Логика предикатов
Если объект высказывания, т.е. о чем говорится в предложении, не определен, то это предложение называют высказывательной функцией. Аргументами высказывательной функции являются предметные переменные, которые обозначают строчными буквами латинского алфавита x, y, z…Эта функция приобретет значение И=1 или Л=0 только при подстановке в высказывательную функцию вместо предметных переменных их конкретных значений. Конкретные значения аргументов высказывательной функции называют предметными постоянными, которые обозначают строчными буквами латинского алфавита а, в, с…
Высказывательную функцию иначе называют предикатом.
Пусть заданы множества Х1, Х2,…, Хk k – местным предикатом на множествах Х1, Х2,…, Хk (функцией – высказыванием от k переменных) называется выражение, содержащее k переменных и превращающееся в высказывание при подстановке вместо этих переменных конкретных элементов из приведенных выше множеств.
Число переменных часто указывается как верхний индекс у предиката.
P (k) (Х1, Х2 ,… , Хk) –k – местный предикат
Разрешимым называется предикат, если существуют наборы конкретных элементов, которые обращают предикат в истинное высказывание.
Если k – местный предикат задан на множествах Х1, Х2,…, Хk , то совокупность данных множеств называется областью определения данного предиката. Подмножества заданных множеств, на которых предикат принимает истинные значения, называется областью истинности данного предиката.
Если предикат при подстановке любых конкретных элементов из соответствующих множеств обращается в истинное (ложное) высказывание, он называется тождественно-истинным (тождественно-ложным).
Если два предиката на всех наборах переменных принимают одинаковые значения, то они называются равносильными.
На предикаты естественным образом переносятся все определения логических операций. Операции отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции вводят для предикатов, определенных на одном и том же множестве. Кроме операций логики высказываний к предикатам применяются кванторные операции:
1. Квантор общности "x (Z (x)) - “для всех x имеет место предикат Z(x)”
2. Квантор существования $ x (Z (x)) - “существует x, для которого имеет место предикат Z (x)”
Применение кванторов превращает одноместный предикат в константу.
Если имеется k – местный предикат Ф (Х1, Х2 ,… , Хk), то можно применять кванторы по какой-либо переменной.
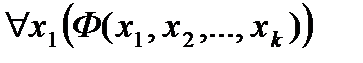
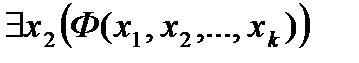
В результате получается (k-1) – местный предикат от (Х1, Х2 ,… , Хk), где переменные к которым относится квантор, называются связанными, а остальные свободными.
Формулой исчисления предикатов называется выражение, составленное из переменных предикатов с помощью логических операций и кванторов и обращающееся в конкретный предикат при подстановке вместо переменных конкретных предикатов.
Все свойства, законы и формулы алгебры логики соответствуют теории предикатов. Законы предикатных формул, содержащих кванторные операции:
| коммутативный закон | "x"y(F2(x, y)) º"y"x(F2(x, y)) $x$y(F2(x, y)) º$y$x(F2(x, y)) только для одноименных кванторов |
| дистрибутивный закон | "x(F1(x))Ù"x(F2(x)) º"x(F1(x)ÙF2(x)) $x(F1(x))Ú$x(F2(x)) º$x(F1(x)ÚF2(x)) для логической связки Ù формул только с кванторами " по одной переменной x. для логической связки Ú формул только с кванторами $ по одной переменной x. |
| закон идемпотентности ÂÎ{";$} | Âx(F(x))Ú Âx(F(x)) º Âx(F(x)) Âx(F(x))ÙÂx(F(x)) º Âx(F(x)) |
| закон исключения третьего | Âx(F(x))Ú 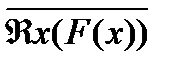 º1, где ÂÎ{";$} º1, где ÂÎ{";$} |
| закон противоречия | Âx(F(x))Ù 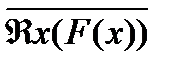 º0, где ÂÎ{";$} º0, где ÂÎ{";$} |
| законы де Моргана | "x( 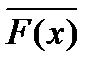 ) º ) º 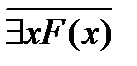 ; $x( ; $x( 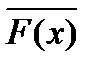 ) º ) º 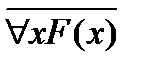 |
| закон двойного отрицания | 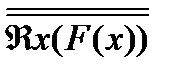 ºÂx(F(x)), где ÂÎ{";$} ºÂx(F(x)), где ÂÎ{";$} |
| свойства констант | Âx(F(x))Ú0ºÂx(F(x)); Âx(F(x))Ú1º1; Âx(F(x))Ù0º0; Âx(F(x))Ù1ºÂx(F(x)), где ÂÎ{";$}. |
Задание.
На множестве М={1, 2,.., 20} заданы предикаты: А(x)={x не делится на 5}, В(x)= {x – четное число}, С(x)={x – число простое}, D(x)= {x – кратно 3}.
Найдите множество истинности следующего предиката:
B(x) → ØA(x)
Решение:
1 Выразим заданную предикатную формулу через основные логические операции и заменим их соответствующими операциями теории множеств:
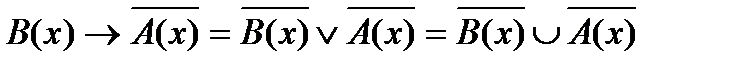
2 Найдем элементы множеств, участвующих в полученной формуле теории множеств:
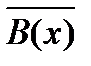 = {1,3,5,7,9,11,13,15,17,19} – нечетные числа множества М
= {1,3,5,7,9,11,13,15,17,19} – нечетные числа множества М
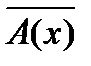 = {5,10,15,20} - числа кратные 5 из множества М
= {5,10,15,20} - числа кратные 5 из множества М
3 Выполним операцию объединения над найденными множествами:
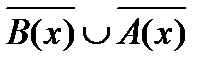 = {1,3,5,7,9,11,13,15,17,19}
= {1,3,5,7,9,11,13,15,17,19}  {5,10,15,20}= {1,3,5,7,9,10,11,13,15,17,19,20}
{5,10,15,20}= {1,3,5,7,9,10,11,13,15,17,19,20}
4 Множеством истинности заданного предиката будет:
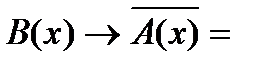 {1,3,5,7,9,10,11,13,15,17,19,20}
{1,3,5,7,9,10,11,13,15,17,19,20}
Теория алгоритмов
Рассмотренные ранее релейно-контактные схемы не дают полного представления о работе дискретного преобразователя информации, поскольку не учитывается тот факт, что реальные устройства работают во времени.
Конечный автомат является математической моделью реальных дискретных устройств по переработке информации. Структура теории конечных автоматов определяется теми задачами, которые возникают при производстве и эксплуатации таких устройств.
Конечным автоматом называется система объектов А = (S, X, Y, p, m), где S, X, Y – произвольные непустые конечные множества, а p и m – отображения вида:
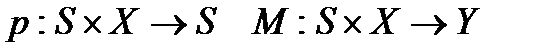
Множество S называется множеством состояний автомата, а его элементы – состояния. Множество X называется входным алфавитом (конечный набор состояний входа автомата), его элементы – входными сигналами, их последовательности – входными словами. Множество Y называется выходным алфавитом, его элементы – выходными сигналами, их последовательности – выходными словами. Отображение p называется функцией переходов, а отображение m - функцией выходов.
С конечным автоматом ассоциируется воображаемое устройство, которое работает следующим образом. Оно может находиться в состоянии из множества S, воспринимать сигналы из множества X и выдавать сигналы из множества Y.
Обозначим состояние, входной и выходной сигналы устройства в момент времени t через S(t), X(t), Y(t) соответственно. Предположим, что эти величины изменяются только в дискретные моменты времени t = 1,2.., причем:
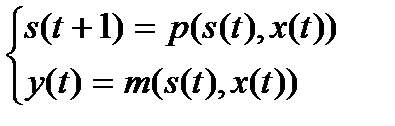
Эти уравнения называются законом функционирования автомата. Если какое-нибудь реальное дискретное устройство работает так, как описанное воображаемое устройство, то оно называется реализацией автомата А.
ВОПРОСЫ К ДИФФЕРЕНЦИРОВАННОМУ ЗАЧЕТУ
1. Высказывания и высказывательные формы. Логическое значение высказывания. Элементарные и составные высказывания.
2. Основные логические операции: отрицание, дизъюнкция, конъюнкция, импликация, эквиваленция.
3. Формулы алгебры логики. Таблица истинности и методика ее построения. Тождественно-истинные (тавтологии) и тождественно-ложные формулы.
4. Понятие равносильные формулы и их свойства. Законы алгебры логики.
5. Методика упрощения формул логики с помощью равносильных преобразований. Методика проверки двух формул на равносильность с помощью их предварительного упрощения. Доказательство тождественной истинности и тождественной ложности формул логики с помощью равносильных преобразований.
6. Понятие бинарное отношение. Примеры и способы задания бинарных отношений. Рефлексивные, симметричные и транзитивные бинарные отношения. Понятие отображение, функция. Типы отображений. Взаимно-однозначные отображения и их свойства. Обратное отображение. Композиция отображений.
7. Понятие подстановка. Тождественная подстановка. Формула количества подстановок. Обратная подстановка. Циклическое разложение подстановки.
8. Понятие функция алгебры логики (булева функция). Способы задания булевой функции. Проблема представления булевой функции в виде формул логики. Свойства совершенства формул логики.
9. Дизъюнктивная нормальная форма (ДНФ). Совершенная ДНФ (СДНФ). Представление булевой функции в виде СДНФ по таблице истинности формулы и с помощью равносильных преобразований.
10. Понятие релейно-контактной схемы. Описание релейно-контактных схем с помощью формул алгебры логики. Методика упрощения релейно-контактных схем с помощью равносильных преобразований формул логики.
11. Понятие выражение одной из булевых функций через другие. Операция двоичного сложения. Многочлен Жегалкина. Представление булевой функции в виде многочлена Жегалкина. Функции Шеффера и Пирса.
12. Понятие множество. Конечные и бесконечные множества, пустое множество. Понятие подмножество. Количество подмножеств конечного множества. Операции над множествами: объединение, пересечение, дополнение, дизъюнктивная сумма, разность. Теоретико-множественные диаграммы Эйлера-Венна.
13. Основные законы алгебры множеств. Формула количества элементов в объединении двух конечных множеств; соответствующая формула для трех множеств; решение задач с помощью этих формул.
14. Декартово произведение множеств. Декартова степень множества. Соотношение между теоретико-множественными и логическими операциями. Перевод теоретико-множественного выражения в соответствующую формулу логики. Методика проверки теоретико-множественных соотношений с помощью формул логики.
15. Понятие предикат. Область определения и область истинности предиката. Обычные логические операции над предикатами. Равносильность предикатов. Следование одного предиката из другого.
16. Кванторные операции над предикатами. Квантор общности и квантор существования. Свободные и связные переменные. Понятие предикатная формула. Равносильность формул логики предикатов. Законы логики предикатов. Определение области истинности для предикатов, содержащих кванторные операции.
17. Формализация математических предложений с помощью логики предикатов: запись математических предложений, определений на языке предикатов. Методика построения отрицания к предикатам, содержащим кванторные операции.
18. Понятие прямая и противоположная теорема. Понятие необходимые и достаточные условия теоремы.
19. Понятие алгоритма. Различные подходы к формализации понятия «алгоритм». Способы представления алгоритмов.
20. Основные алгоритмические конструкции: композиция, альтернатива, итерация. Понятие машины Поста. Команды машины Поста.
ЛИТЕРАТУРА
Основные источники:
1. Гончарова Г.А., Мочалин А.А. Элементы дискретной математики. - М: ФОРУМ-М, 2009
2. Новиков Ф.А. Дискретная математика для программистов: - СПб.: Питер, 2007
Дополнительные источники:
3. Акимов О.Е. Дискретная математика: логика, группы, графы. - М: Лаборатория базовых знаний, 2011
4. Ерусалимский Я.М. Excel: Дискретная математика: теория, задачи, приложения. - М.: Вузовская книга, 209
5. Яблонский С.В. Введение в дискретную математику. – М.: Высшая школа, 208
РЕЦЕНЗИЯ
Методические указания к выполнению домашней контрольной работы предназначены для реализации требований к минимуму содержания и уровня подготовки студентов заочной формы обучения по специальностям 09.02.03 «Программирование в компьютерных системах» и 09.02.02 «Компьютерные сети».
Выполнение домашней контрольной работы опирается на знания, полученные студентами на занятиях по дисциплине «Элементы математической логики» и позволяет закрепить, дополнить и углубить эти знания.
Реализация данных методических указаний обеспечивает получение студентами практических навыков, позволяющих им самостоятельно решать прикладные задачи математики, умение быстро ориентироваться в выборе методов их решения. В целом содержание методических указаний соответствует рабочей программе по дисциплине и отвечает государственному образовательному стандарту по специальностям 09.02.03 и 09.02.02. Методические указания могут быть использованы на занятиях по дисциплине «Элементы математической логики».
Преподаватель
электромеханического колледжа
Воронежского филиала МИИТ Н.Н. Коноплина