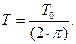Звено второго порядка (колебательное звено)

Такие звенья описываются дифференциальным уравнением вида:

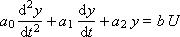
Если на вход звена подать единичную функцию Хэвисайда от времени 1[t], при нулевых начальных условиях системы, то реакция на выходе будет называться переходной функцией (или переходной характеристикой), которую часто обозначают как h(t). Сигнал 1[t] — это, в некотором смысле, эталонный испытательный сигнал. Существуют и другие эталонные испытательные сигналы. Например, бесконечный импульс нулевой длины (дельта-функция Дирака), гармонический сигнал, периодические прямоугольные импульсы.

Преобразуем по Лапласу это уравнение:

a0 · p2 · Y(p) + a1 · p · Y(p) + a2 · Y(p) = b · U(p)

или, иначе:

(a0 · p2 + a1 · p + a2) · Y(p) = b · U(p).

Определим передаточную функцию звена:

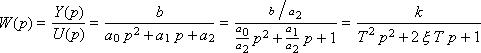
Если записать уравнение без входного воздействия (нулевые входные воздействия U = 0) и сократить Y, то есть: T2p2 + 2ξTp + 1 = 0, то такое уравнение будет называться характеристическим, поскольку характеризует исключительно внутренние свойства звена. Обратите внимание, что в записи звена содержатся три параметра:

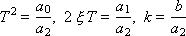
T — постоянная времени (в секундах);

ξ — коэффициент затухания (безразмерная величина);

k — передаточный коэффициент.

В зависимости от величины ξ звенья второго порядка классифицируются по видам:

ξ = 0 — консервативное звено второго порядка;

0 < ξ < 1 — колебательное звено второго порядка;

ξ ≥ 1 — апериодическое звено второго порядка.

Апериодическое звено 2-го порядка (ξ ≥ 1)

Характеристическое уравнение звена следующее:

T2p2 + 2ξTp + 1 = 0.

И оно имеет действительные отрицательные корни:

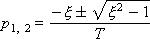
Данное звено можно представить в виде последовательно соединенных звеньев с различными постоянными времени:

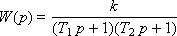
Tогда при T1 > T2 переходная характеристика звена имеет вид:

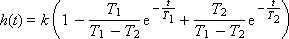
То есть, в решении присутствуют затухающие экспоненты. Типичное поведение звена с такими параметрами показано на рис. 7.6.

Рис. 7.6. Реакция апериодического звена на единичный входной сигнал

В частном случае, когда ξ = 1, оба корня будут одинаковыми, отрицательными:

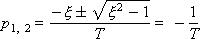
Колебательное звено 2-го порядка (0 < ξ < 1)

Характеристическое уравнение звена следующее:

T2p2 + 2ξTp + 1 = 0.

Корни разные, комплексно-сопряженные, с отрицательной вещественной частью:

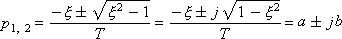
, где a = –ξ/T, b = sqrt(1 – ξ2)/T.

Так как корни мнимые, то в поведении звена присутствует колебательная составляющая. Именно за эту особенность поведения звено получило название колебательного (см. рис. 7.7 и рис. 7.8).

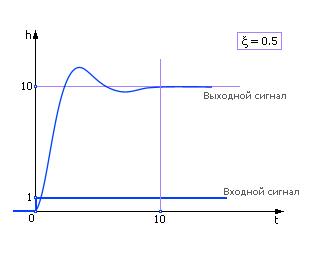
Рис. 7.7. Реакция колебательного звена на входной единичный сигнал (ξ = 0.5)

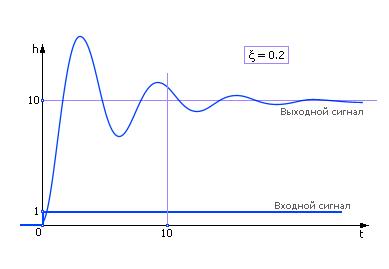
Рис. 7.8. Реакция колебательного звена на входной единичный сигнал (ξ = 0.2)

Из графиков видно, что с ростом ξ колебательность звена уменьшается, исчезая при ξ ≥ 1

Переходная функция звена имеет вид:

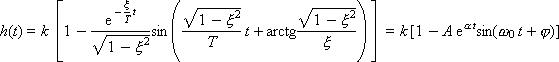
где

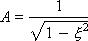
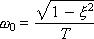
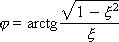
При малых ξ значение A приближается к 1, а значение φ — к 90°. По физическому смыслу ω0 представляет собой собственную частоту колебаний.

Консервативное звено 2-го порядка (ξ = 0)

Характеристическое уравнение звена следующее:

T2p2 + 1 = 0.

Корни одинаковые, комплексно-сопряженные, с нулевой вещественной частью:

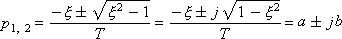
Так как корни чисто мнимые, то поведением звена являются незатухающие колебания (ξ = 0), см. рис. 7.9.

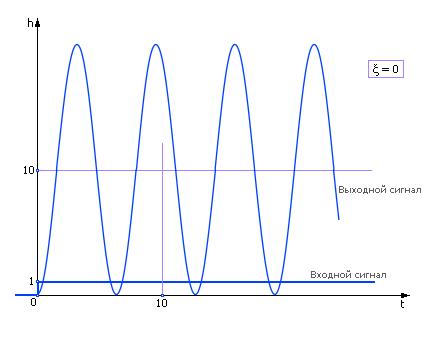
Рис. 7.9. Реакция колебательного звена на входной единичный сигнал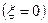

Переходная функция звена имеет вид: .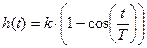

Из графика экспериментальным путем можно определить единственный параметр