Методы решения задач о раскрое

КУРСОВАЯ РАБОТА

На тему	“Задача о раскрое”
Студент
	подпись	дата	инициалы, фамилия
Группа	9ПО101
Специальность	Программное обеспечение вычислительной техники и автоматизированных систем
	шифр, название
Руководитель
	подпись	дата	инициалы, фамилия

Барнаул 2013

Содержание

Введение 3

1Сущность задач о раскрое 5

1.1 Характеристика симплекс-метода, применимого для решения задачи 8

1.2 Аналитическое решение задачи в общем виде 12

2 Решение задачи о раскрое 14

Заключение 19

Список литературы 20

Введение

Цель курсовой работы решить задачу о раскрое.

Основной задачей курсовой работы является рассмотрение моделей задач о раскрое, а также решение их симплекс-методом.

В глобальной системе управления народным хозяйством страны планирование деятельности предприятия является чрезвычайно важным звеном, определяющим в конечном счёте результативность функционирования системы в целом. Именно на этом уровне управления осуществляется соединение основных составляющих производства – средств труда, предметов труда и самого труда, устанавливается и поддерживается необходимая пропорциональность между ними, что обеспечивает рациональность использования предприятием имеющихся ресурсов.

Особенностью решения задач планирования является необходимость учёта при их решении множества переменных величин, характеризующих постоянно изменяющиеся производственные условия. А так как число сочетаний этих величин в течение определённого времени – планового периода – может быть достаточно большим, то возможно существование значительного числа вариантов плановых решений. Отсюда большая размерность решаемых плановых задач. И, тем не менее, необходимо получить оптимальное, или близкое к нему решение. В этих условиях простой перебор и сравнение всех возможных вариантов решения конкретной плановой задачи нереальны из-за большой трудоёмкости вычислений. Поэтому требуются специальные методы, позволяющие в приемлемые сроки с достаточной степенью обоснованности с учётом особенностей конкретного производства выйти на искомое решение.

Эффективное применение этих методов требует, прежде всего, их серьёзного и глубокого изучения, а значит определённой систематики и классификации. Любая классификация подчинена целям исследования или анализа того или иного явления. В соответствии с целью выбирается и классификационный признак. Поскольку целью изучения экономико-математических методов является раскрытие механизма их реализации, определение области наиболее эффективного использования, то в качестве классификационного признака можно принять, например, характер используемого математического аппарата. По этому признаку можно выделить методы классической и прикладной математики.

Методы классической математики включают математический анализ и теорию вероятностей.

Группа методов прикладной математики обширна по номенклатуре. Включаемые в неё методы неоднородны по составу элементарных расчётов, способам их реализации, применяемым приёмам и т. д. По общности указанных признаков методы рассматриваемой группы можно далее классифицировать следующим образом: оптимального, линейного программирования, математической статистики, комбинаторные, теории расписаний, игр, массового обслуживания, управления запасами, экспертных оценок.

Оптимальное программирование – это комплекс специальных методов, обеспечивающих в условиях множества возможных решений выбор такого, которое является наилучшим (оптимальным) по заданному критерию при определённых ограничительных условиях. Оптимальное программирование – действенный инструмент эффективного решения задач управления. В их числе – линейное, нелинейное, динамическое, целочисленное программирование и др.

Линейное программирование используется при решении задач в том случае, когда целевая функция и ограничительные условия выражены линейными зависимостями. Отыскиваемые при этом неизвестные переменные обеспечивают экстремум целевой функции.

Методы решения задач о раскрое

В настоящее время известен ряд работ по раскрою, в которых обычно используется метод индексов Л.В. Канторовича и симплекс-метод Д. Данцига или его модификации. Этими методами пользуются, чтобы найти оптимальный план раскроя, когда известны все возможные его варианты. Следует отметить, что работа по составлению всех раскроев (особенно когда число различных заготовок и исходного проката велико) трудоёмка и продолжительна – в итоге получается линейная задача с большим числом неизвестных, решение которой возможно только с использованием ЭВМ.

Решение задач раскроя линейных материалов без составления всех исходных вариантов с использованием методов динамического программирования было получено П. Гилмором и Р. Гомори. Идея предполагаемого способа близка к идее метода разложения Д. Данцига и Ф. Вульфа. Она заключается в том, что после каждого шага симплекс-метода для выявления метода улучшения раскроя решается небольшая вспомогательная задача. В данном случае она оказывается задачей «о ранце» и для её решения применяются методы диагностического программирования.

Задача о раскрое формулируется следующим образом.

Необходимо из листа проката размером M*N выкроить заготовки площадью m*n в заданном количестве p_i(i=1,2,…,k). Требуется определить оптимальный план раскроя листа, т.е. получить минимальные отходы с учётом комплектности заготовок. Показателем, определяющим экономичность раскроя, является коэффициент раскроя, рассчитываемый по формуле:

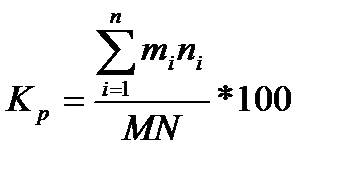, где

m_i- длина i-й заготовки, мм.;

n_i– ширина i-й заготовки, мм.;

M,N – соответственно длина и ширина исходного листа.

Когда требуется определить оптимальный план раскроя листового проката, прежде всего определяются коэффициенты раскроя K_p, которыми характеризуется экономичность раскроя. Этот коэффициент представляет собой отношение площади заготовок к площади листа и рассчитывается по формуле.

При создании математической модели задачи раскроя необходимо учитывать ряд требований, связанных с производством: число заготовок, полученных по определённым раскроям, должно соответствовать установленной производственной программе; общее количество материалов, израсходованных на выполнение производственной программы, или величина отходов, полученных от раскроя по выбранным вариантам должны быть наименьшими; при этом в обоих случаях получаемые решения будут равноценными.

Варианты раскроя образуются путём комбинирования различных заготовок во всех возможных сочетаниях. При таком комбинировании даже при незначительном увеличении числа видов заготовок характерен быстрый рост числа возможных сочетаний, т.е. возможных вариантов раскроя. С увеличением числа вариантов раскроя сильно увеличивается размерность задачи линейного программирования, что приводит к резкому возрастанию общего времени решения задачи на ЭВМ.

Для сокращения времени решения задачи на ЭВМ искусственно вводится число вариантов раскроя. Это приводит к тому, что набор вариантов выбирается из меньшего числа и уже не даёт уверенности в том, что найден действительно самый лучший вариант раскроя.

Кроме симплекс-метода существует также эвристический метод решения задач о раскрое материалов. Эвристические методы являются методами решения задач, построенными на использовании правил, приёмов, упрощений, обобщающих прошлый опыт решающего. Эвристическое рассуждение – предварительное правдоподобное рассуждение, направленное на поиск решения задач определённого класса. Эвристические рассуждения и методы строятся на использовании аналогии отдельных практических приёмов специалиста (технолога, плановика, диспетчера и др.) и на логическом умозаключении от частных, единичных случаев к обобщениям.

Важно знать, что эвристические методы учитывают необходимые технологические ограничения, порождаемые главным образом особенностями холодноштамповочного производства деталей, они требуют минимального времени просчёта задач на ЭВМ при достаточно высоком коэффициенте раскроя.