Тема 2. Системы линейных уравнений

Разберите решение задачи 2.

Задача 2. Решить методом Гаусса систему уравнений.

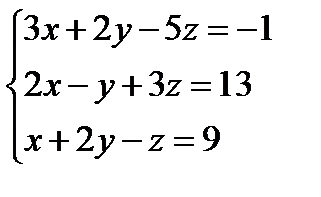
Решение:

Запишем расширенную матрицу системы, и с помощью элементарных преобразований приведем эту матрицу к ступенчатому виду:

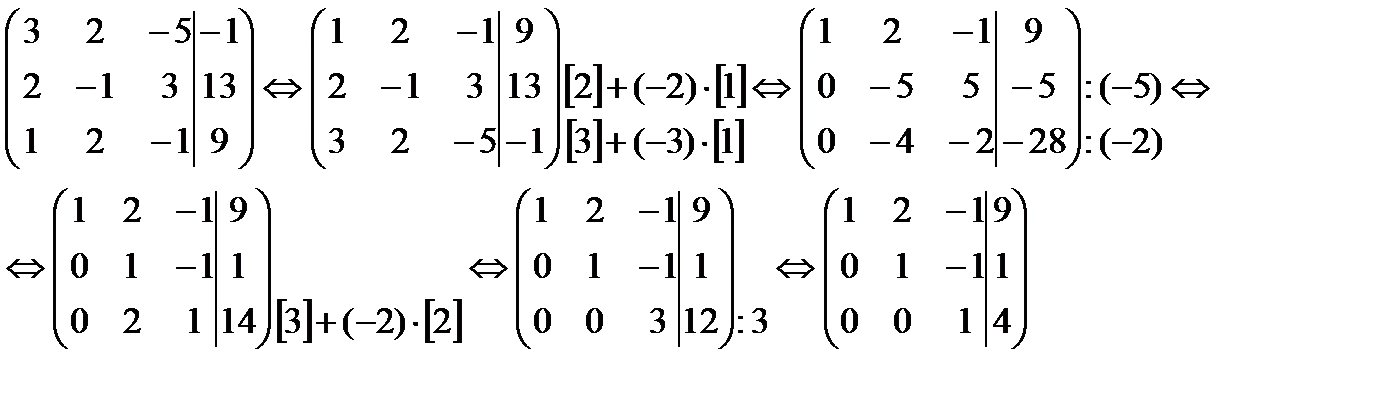
Пояснения к преобразованиям:

Сначала смотрим на левое верхнее число:

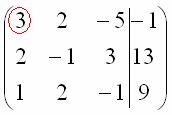
Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

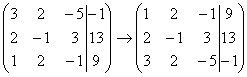
Теперь первая строка у нас останется неизменной до конца решения. Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

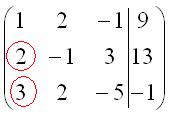
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:

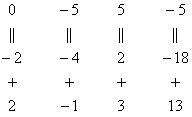
Результат записываем во вторую строку:

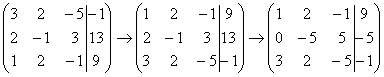
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3:

Результат записываем в третью строку:

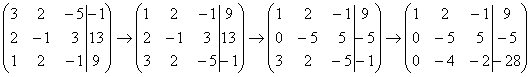
Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО:

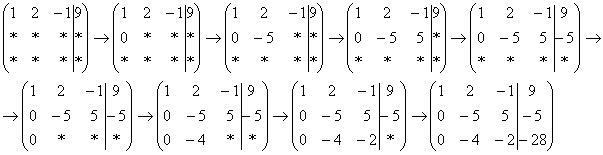
Далее нужно получить единицу на следующей «ступеньке»:

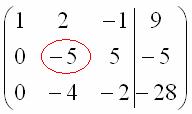
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

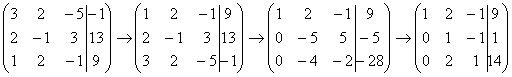
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

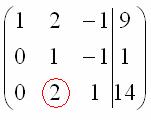
Для этого к третьей строке прибавляем вторую строку, умноженную на –2:

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:

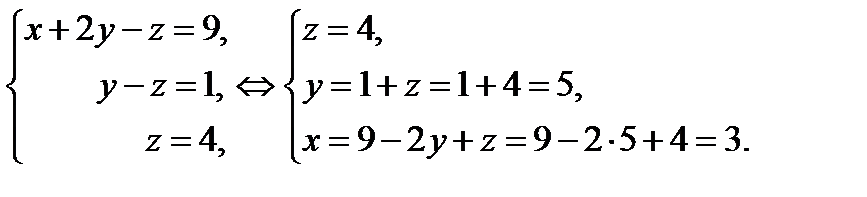
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат: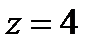

Смотрим на второе уравнение: 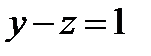. Значение «зет» уже известно, таким образом: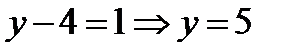

И, наконец, первое уравнение: 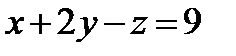. «Игрек» и «зет» известны, дело за малым: .

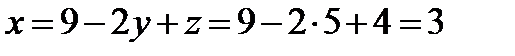Ответ: .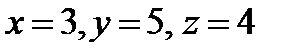

Вопросы для самопроверки

1. Что называют системой линейных уравнений?

2. Напишите формулу Крамера решения системы линейных уравнений. В каких случаях их можно использовать?

3. Назовите схему решения системы линейных уравнений по методу Гаусса?

4. Сформулируйте теорему Кронекера-Капели?

5. Опишите матричный способ решения системы линейных уравнений?

6. В чем заключается суть метода Гаусса решения системы линейных уравнений?

7. Какова геометрическая интерпретация системы линейных уравнений и неравенств?