Краткие теоретические сведения
Лабораторная работа 1
«Обработка статистических данных»
Цель:Статистическая обработка данных.
Задачи:
· построение интервального вариационного ряда;
· графическое изображение ряда;
· вычисление точечных оценок.
Оборудование:компьютер.
Краткие теоретические сведения
Под генеральной совокупностью подразумеваются все возможные наблюдения некоторого качественного или количественного показателя (признака), все исходы случайного испытания или вся совокупность реализаций случайной величины Х.
На практике в большинстве случаев основным и часто единственным возможным является выборочный метод исследования. Он основан на том, что из всей генеральной совокупности случайно отбирают часть элементов. Эта выбранная часть элементов называется выборкой, а число элементов этой выборки называют объемом.
Наблюдаемые в процессе выборки значения 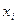 случайной величины Х называются вариантами. Обычно полученные наблюдаемые значения (варианты) представляют собой множество расположенных в беспорядке чисел. Для изучения закономерностей значений варьирования (изменения) значений случайной величины опытные данные подвергаются обработке. Для этого прежде всего результаты наблюдений случайной величины (варианты) ранжируют, т. е. располагают в порядке возрастания. Разность между максимальными и минимальными вариантами называется размахом выборки.
случайной величины Х называются вариантами. Обычно полученные наблюдаемые значения (варианты) представляют собой множество расположенных в беспорядке чисел. Для изучения закономерностей значений варьирования (изменения) значений случайной величины опытные данные подвергаются обработке. Для этого прежде всего результаты наблюдений случайной величины (варианты) ранжируют, т. е. располагают в порядке возрастания. Разность между максимальными и минимальными вариантами называется размахом выборки.
Следующим этапом обработки опытных данных является подсчет частот, с которыми встречаются различные варианты 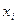 . Пусть из генеральной совокупности извлечена выборка объема
. Пусть из генеральной совокупности извлечена выборка объема 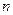 , причем вариант
, причем вариант 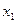 наблюдался
наблюдался 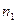 раз,
раз, 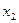 -
- 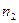 раз, …,
раз, …, 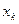 -
- 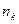 раз, где
раз, где 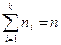 . Количественными характеристиками варианты
. Количественными характеристиками варианты 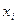 являются частота, равная числу
являются частота, равная числу 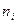 вариант
вариант 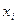 в выборке объема
в выборке объема 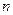 , и относительная частота
, и относительная частота 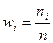 . Очевидно, что сумма относительных частот равна единице:
. Очевидно, что сумма относительных частот равна единице: 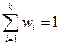 .
.
При изучении дискретных случайных величин большое значение имеет закон (ряд) распределения задаваемый в виде таблицы, в которой установлено соответствие всеми возможными значениями 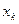 случайной величины Х и их вероятностями
случайной величины Х и их вероятностями 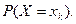 В математической статистике аналогично устанавливаются соответствия между наблюдаемыми значениями и их частотами или относительными частотами. Так полученная последовательность пар
В математической статистике аналогично устанавливаются соответствия между наблюдаемыми значениями и их частотами или относительными частотами. Так полученная последовательность пар 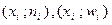 вариантов и соответствующих им частот называется дискретным вариационным рядом, который располагают в виде таблиц.
вариантов и соответствующих им частот называется дискретным вариационным рядом, который располагают в виде таблиц.
Для дискретной случайной величины, число возможных значений которой велико, построение дискретного вариационного ряда нецелесообразно. В подобных случаях следует строить интервальный вариационный ряд распределения. Для построения такого ряда весь интервал варьирования наблюдаемых значений случайной величины разбивается на ряд частичных интервалов и подсчитывается частота попадания значений величины в каждый частичный интервал.
Для определения величины (длины) частичного интервала можно воспользоваться формулой Стерджеса:
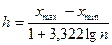 .
.
При этом длина частичного интервала определяется с той же точностью, что и исходные данные. За начало первого интервала рекомендуется брать величину 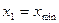 . Правая граница последнего интервала
. Правая граница последнего интервала 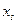 должна удовлетворять неравенству
должна удовлетворять неравенству 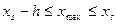 . Границы промежуточных интервалов определяются прибавлением к правой границе предыдущего интервала длины частичного интервала h.
. Границы промежуточных интервалов определяются прибавлением к правой границе предыдущего интервала длины частичного интервала h.
При вычислении относительных частот округление результатов следует проводить таким образом, чтобы их сумма была рана 1. Иногда интервальный вариационный ряд для простоты исследований условно заменяют дискретным. В этом случае серединное значение i – го интервала принимают за вариант 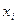 , а соответствующую интервальную частоту
, а соответствующую интервальную частоту 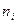 - за частоту варианта. Серединное значение i – го интервала
- за частоту варианта. Серединное значение i – го интервала 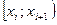 определяется по формуле
определяется по формуле 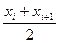 .
.
Наблюдаемые значения случайной величины, представленные в виде вариационного ряда, можно изображать графически, а именно в виде полигона и гистограммы.
Полигон используют для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами 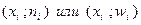 (масштабы по осям различны).
(масштабы по осям различны).
Гистограмма служит только для изображения интервальных вариационных рядов. Для её построения в прямоугольной системе координат на оси абсцисс откладывают отрезки, изображающие частичные интервалы варьирования, и на этих отрезках, как на основаниях строят прямоугольники с высотами, равными отношениям 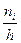 или
или 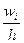 . Эти отношения называются плотностями частот и относительных частот соответственно.
. Эти отношения называются плотностями частот и относительных частот соответственно.
Для выборки объема 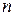 , в которой число различных значений признака равно
, в которой число различных значений признака равно 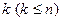 , статистические оценки (
, статистические оценки ( 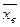 - выборочное среднее;
- выборочное среднее; 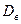 - выборочная дисперсия;
- выборочная дисперсия; 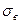 - выборочное стандартное отклонение; V - коэффициент вариации) вычисляются по формулам:
- выборочное стандартное отклонение; V - коэффициент вариации) вычисляются по формулам:
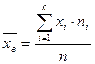 ;
; 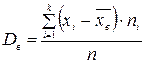 ;
; 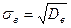 ;
; 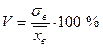 .
.
Контрольные вопросы
1. Что называется генеральной совокупностью?
2. Что называется выборкой?
3. Что называется вариантой?
4. Что называется размахом выборки?
5. Что называется вариационным рядом?
6. Что называется интервальным вариационным рядом?
7. Что называется полигоном распределения?
8. Что называется гистограммой распределения?
9. Что называется точечной оценкой?
10. По каким формулам вычисляются точечные оценки?
Рекомендуемая литература
1. Красс М.С. Математика для экономических специальностей. – М: ИНФРА – М, 1998
2. Ермаков В.И. Общий курс высшей математики (для экономистов). – М: ИНФРА – М, 2001
3. Кремер Н.Ш. Высшая математика для экономистов. – М: ЮНИТИ - 2000
4. Данко П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов : В 2 ч. Ч 1,2 – М.: ОНИКС 21 век, 2003
5. 7Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1972
6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979
Лабораторная работа 2
«Проверка статистических гипотез»
Цель:Статистическая обработка данных.
Задачи:
· вычисление теоретических частот признаков;
· проверка согласования нормального закона распределения с помощью критерия согласия Пирсона;
· нахождение доверительного интервала для оценки ожидаемого среднего значения признаков.
Оборудование:компьютер.
