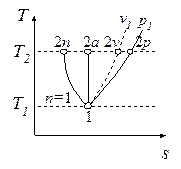Изотермический процесс

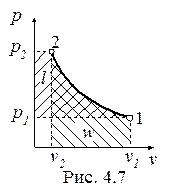Дано: параметры начального состояния p₁, v₁, давление конечного состояния p₂ (p₂ > p₁).

Определить: недостающие термические параметры T₁ и v₂, работу и теплоту процесса (w, l, q).

Изотермический процесс, построенный на основании исходных данных (p₁, v₁, p₂) в диаграммах p-v и T-s, представлен на рис. 4.7 и 4.8.

Из уравнения состояния для точки 1 определяет-

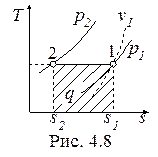ся температура T = p₁^.v₁/R. Сравнение уравнений состояния для точек 1 и 2 при условии T₁ = T₂ = T = const (p₁^.v₁ = RT, p₂^.v₂ = RT) дает связь между давлением и объемом в изотермическом процессе:

,

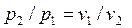(4.38)

из которой можно определить удельный объем v₂.

Формулы для расчета работы и теплоты изотермического процесса получены на основании уравнений:

.

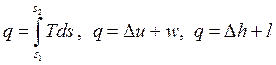Для идеального газа при T = const имеем

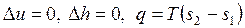,	(4.39)
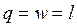,	(4.40)
.

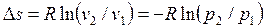Для расчета теплоты (работы) изотермического процесса можно использовать формулы

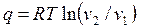,	(4.41)
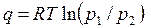.	(4.42)

Работа и теплота изотермического процесса в p-v- и T-s- диаграммах представлена заштрихованными площадями. Равенство работ w и l подтверждается симметрией изотермы относительно осей координат. Работа процесса w < 0, т.к. v₂ < v₁; работа l < 0, поскольку p₂ > p₁; теплота отводится (q < 0), т.к. s₂ < s₁.

Адиабатный процесс

Адиабатным называется процесс, который протекает без теплообмена с окружающей средой (dq = 0).

В обратимых адиабатных процессах энтропия не изменяется (ds = 0,
s = const), в необратимых - энтропия увеличивается (ds > 0).

Уравнение обратимого адиабатного процесса имеет вид

,

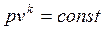(4.43)

где k – показатель адиабаты.

Для идеального газа

.

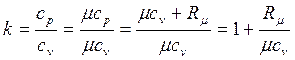(4.44)

Для одноатомного идеального газа показатель адиабаты не зависит от температуры:

.

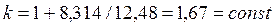Для двух-, трех- и многоатомных идеальных газов k = f(T), т.к. теплоемкость mc_v =f(T). С увеличением температуры показатель адиабаты убывает.

Если принять теплоемкость постоянной в соответствии молекулярно-кинетической теорией газов, то для двухатомных газов

,

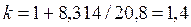для трех- и многоатомных газов:

.

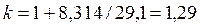Расчет адиабатных процессов двух-, трех- и многоатомных газов при значениях показателя адиабаты 1,4; 1,29 является приближенным, т.к. не учитывает зависимость теплоемкости от температуры.

Совместное решение (4.43) с уравнением состояния идеального газа
pv = RT дает следующие связи параметров:

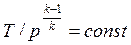,	(4.45)
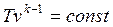.	(4.46)

Для адиабатного процесса 1-2, в котором параметры изменяются от p₁, v₁, T₁ до p₂, v₂, T₂, на основании уравнений (4.43), (4.45), (4.46) можно получить следующие соотношения между параметрами:

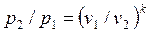,	(4.47)
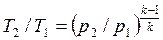,	(4.48)
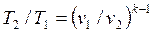.	(4.49)

Совместное решение уравнений

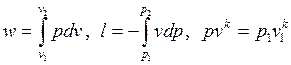
позволяет получить расчетные формулы для работы адиабатного процесса
1-2:

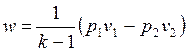,	(4.50)
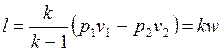.	(4.51)

С учетом уравнения состояния pv = RT, а также соотношения (4.48) формулу (4.50) можно представить следующим образом:

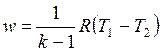,	(4.52)
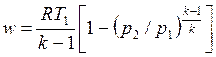.	(4.53)

По формулам (4.46) - (4.53) производят расчеты адиабатных процессов одноатомного идеального газа и приближенные расчеты двух-, трех- и многоатомных газов при значениях k = 1,4, k = 1,29.

Расчет адиабатных процессов с учетом зависимости k = f(T) по вышеприведенным формулам прост, если известны температуры T₁ и T₂. В противном случае используется метод последовательных приближений, что значительно усложняет расчет.

Более простым является табличный метод расчета адиабатного процесса идеального газа с учетом зависимости теплоемкости от температуры. В основе расчета лежат следующие уравнения:

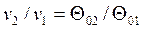,	(4.54)
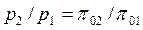,	(4.55)
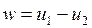,	(4.56)
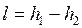.	(4.57)

Здесь 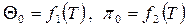- безразмерные величины, приведенные в таблицах термодинамических свойств газов [7], h, u - табличные значения параметров.

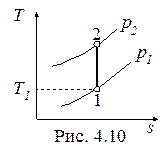
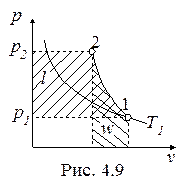Обратимый адиабатный процесссжатия идеального газа, построенный по исходным параметрам p₁, T₁, p₂ в p-v- и T-s- диаграммах, представлен на рис.4.9 и 4.10.

В p-v- диаграмме адиабата - несимметричная гипербола располагается круче изотермы, в T-s- диаграмме – изоэнтропа (s = const, q = 0).

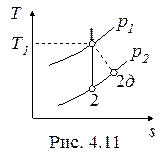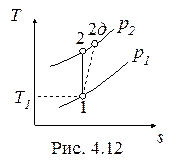Необратимые адиабатные процессы (1-2д), протекающие с увеличением энтропии, показаны на рис. 4.11, 4.12.

Работа необратимого адиабатного расширения (рис.4.11) равна

,

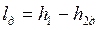и она меньше работы обратимого процесса, вычисляемого по формуле

.

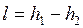Напротив, работа необратимого адиабатного сжатия (рис. 4.12), равная

,

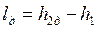больше работы обратимого процесса

.

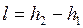Политропные процессы

Политропные процессы описываются уравнением

,

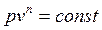(4.58)

где n – показатель политропы, который не зависит от температуры (n = const) и изменяется в пределах от -µ до µ.

Внешняя схожесть уравнений (4.43) и (4.58) позволяет записать расчетные формулы политропного процесса, аналогичные адиабатному:

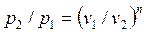,	(4.59)
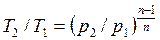,	(4.60)
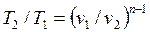,	(4.61)
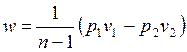,	(4.62)
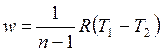,	(4.63)
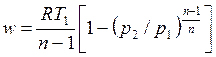,	(4.64)
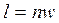.	(4.65)

Теплота политропного процесса рассчитывается по уравнению

,

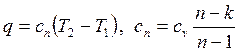(4.66)

где c_n – теплоемкость политропного процесса.

Все многообразие процессов можно описать политропой с показателем -µ < n < µ. Изохорный, изобарный, изотермический, адиабатный процессы являются частным случаем политропных процессов с определенным показателем n. Подставляя конкретные его значения в формулы (4.58) и (4.66), можно доказать, что при:

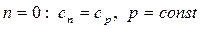- процесс изобарный;

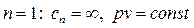- процесс изотермический;

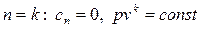- процесс адиабатный;

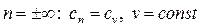- процесс изохорный.

На рис. 4.13 и 4.14 в p-v- и T-s- диаграммах представлено все множество политропных процессов с показателем n, изменяющиxся от -µ до µ.

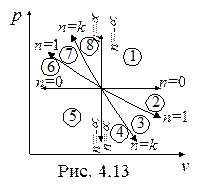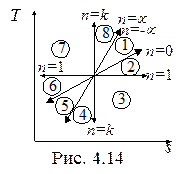Можно выделить следующие группы процессов:

1. Процессы расширения (dv > 0, dw > 0)- области 1, 2, 3, 4.

2. Процессы сжатия (dv < 0, dw < 0) – области 5, 6, 7, 8.

3. Процессы подвода теплоты (ds > 0, dq > 0) – области 8, 1, 2, 3.

4. Процессы отвода теплоты (ds < 0, dq < 0) - области 4, 5, 6, 7.

5. Процессы, протекающие с увеличением температуры (dT > 0, du > 0, dh > 0) - области 7, 8, 1, 2.

6. Процессы, протекающие с уменьшением температуры (dT < 0, du < 0, dh <0) - области 3, 4, 5, 6.

7. Процессы с отрицательной теплоемкостью (c_n < 0, 1 < n < k) - области 3, 7.

В области 3 при подводе теплоты (dq > 0) температура, внутренняя энергия, энтальпия уменьшаются (dT < 0, du < 0, dh < 0). В области 7 при отводе теплоты (dq < 0) температура, внутренняя энергия, энтальпия увеличиваются (dT > 0, du > 0, dh > 0). Это может быть только при отрицательной теплоемкости. В процессах с отрицательной теплоемкостью 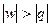, поэтому на производство работы при расширении тратится не только подводимая теплота, но и часть внутренней энергии рабочего тела, а затрачиваемая работа на сжатие компенсирует не только отводимую теплоту, но и повышает внутреннюю энергию рабочего тела.

При изображении политропных процессов в диаграммах p-v и T-s необходимо определить область, к которой они принадлежат, путем сравнения показателя политропы с n = k, n =1 и т.д.

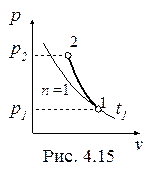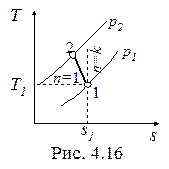Политропный процесс газа с показателем 1<n<k, построенный по исходным параметрам p₁, t₁, p₂ (p₂ > p₁) в p-v- и T-s- диаграммах представлен на рис. 4.15 и 4.16.

В p-v- диаграмме политропа – несимметричная гипербола, которая располагается круче изотермы, т.к. n >1.

В T-s- диаграмме политропа - логарифмическая кривая, которая располагается между изотермой и изоэнтропой, т.к. 1< n < k.

Методические указания

При расчетах изменения калорических параметров (Du, Dh, Ds), теплоты и работы в процессах идеального газа в одних случаях допускается подставлять температуру как в градусах Цельсия, так и в градусах Кельвина, например 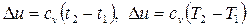, в других - только в градусах Кельвина, например

.

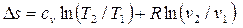В одних величинах допускается при записи размерности использовать как градусы Цельсия (⁰С), так и градусы Кельвина (К), например, удельной теплоемкости,

с, Дж/(кг^.0С), или с, Дж/(кг^.К),

в других - только градусы Кельвина, например, удельной газовой постоянной и энтропии,

R, Дж/(кг^.К), s, Дж/(кг^.К).

Почему это так?

Дифференцирование связи температур

T = t + 273,15

дает dT = dt, т.е. разность температур в абсолютной шкале и в стоградусной шкале одна и та же. Это значит, что цена одного градуса в обеих шкалах одинакова. Следовательно, когда речь идет о разности температур, правомерно использовать любые градусы:

.

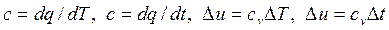В тех случаях, когда речь идет о температуре или об отношении температур,

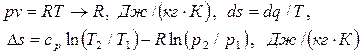
температура подставляется только в градусах Кельвина.

Задачи

1. При сжатии в компрессоре параметры воздуха изменились от p₁ =1 бар, t₁ = 20 ⁰С, до p₂ = 6 бар , t₂ = 440 ⁰С. Рассчитайте изменение энтальпии (Dh), внутренней энергии (Du), энтропии (Ds):

а) используя таблицы термодинамических свойств газов [7]; таблица для воздуха дана в Приложении.

б) при постоянной теплоемкости, принятой согласно молекулярно-кинетической теории газов.

2. Рассчитайте изменение энтальпии воздуха при нагреве его от 0 до
300 ⁰С:

а) используя формулу зависимости теплоемкости от температуры для воздуха

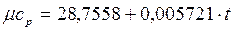, кДж/(кмоль^.0С);

б) используя табличные значения средних теплоемкостей c_pm (см. Приложение).

3. Рассчитайте эксергию потока гелия с параметрами p= 6 бар, t = 400 ⁰С. Параметры окружающей среды: t_oc = 20 ⁰С, p_oc = 1 бар. Мольная масса гелия m = 4 кг/кмоль.

Решение

Эксергия потока гелия

.

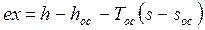Поскольку гелий - одноатомный газ, его теплоемкость постоянна и равна:

.

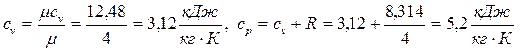Тогда

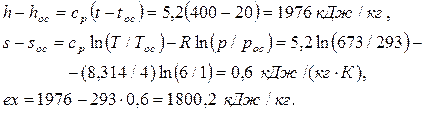
Ответ: ex= 1800,2 кДж/кг.

4. Параметры воздуха изменились от p₁ = 1 бар, t₁ = 0 ⁰С до t₂ = 200 ⁰С:

а) в изобарном процессе;

б) в изохорном;

в) в адиабатном;

г) в политропном с показателем n = 1,2.

Определите для каждого из процессов показатель политропы (n), теплоемкость (c), изменение энтропии (Ds), теплоту (q). Представьте процессы в
T-s- диаграмме.

Теплоемкость принять постоянной согласно молекулярно-кинетической теории газов.

5. При адиабатном сжатии параметры воздуха изменились от p₁ = 1 бар, t₁ = 10 ⁰С до p₂ = 30 бар.

Определите конечную температуру воздуха для случаев:

а) с учетом зависимости теплоемкости от температуры, используя табличные значения p₀;

б) без учета зависимости теплоемкости от температуры, приняв ее постоянной, согласно молекулярно-кинетической теории газов.

Решение

1. Из табл. 2 Приложения для воздуха при t₁ = 10 ⁰С берется значение p₀₁ =1,1323.

С помощью соотношения (4.55) рассчитывается

.

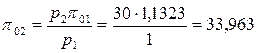По значению p₀₂ из таблицы находится t₂ = 458,5 ⁰С.

2. Температура воздуха рассчитывается по соотношению (4.48) при
k = 1,4:

.

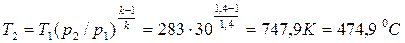Ответ: а) t₂ = 458,5 ⁰С; б) t₂ = 474,9 ⁰С.

Ответы

1. а) Dh= 434 кДж/кг, Du= 313,6 кДж/кг, Ds = 0,4 кДж/(кг×К) ;

б) Dh= 420 кДж/кг, Du= 301,1 кДж/кг, Ds= 0,376 кДж/(кг×К).

2.а) Dh= 306,4 кДж/кг, б) Dh= 305,7 кДж/кг.

4.

Процессы	n	c, кДж/(кг..К)	D s, кДж/(кг.К)	q, кДж/кг
Изобарный			0,55
Изохорный	µ	0,72	0,396	79,2
Адиабатный	1,4
Политропный	1,2	-0,72	-0,396	-79,2

T-s- диаграмма

РЕАЛЬНЫЕ ГАЗЫ И ПАРЫ

Об особенностях реальных газов по сравнению с идеальными, об уравнении состояния и сложности его использования для инженерных расчетов упоминалось в гл. 1.

Настоящая глава посвящена водяному пару, который широко применяется во многих технологических процессах и, прежде всего, в теплоэнергетике, где он является основным рабочим телом.

5.1. Фазовая p-v-T-диаграмма воды и водяного пара

Рассматривается процесс получения пара из воды, залитой в цилиндр (рис. 5.1).

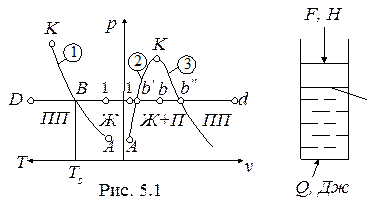
S, м²

Обозначения: 1-линия парообразования; 2- линия кипящей жидкости (нижняя пограничная кривая); 3- линия сухого насыщенного пара (верхняя пограничная кривая); А - тройная точка; К- критическая точка;
Ж– жидкость; П- сухой насыщенный пар; ПП- перегретый пар;
T_s- температура насыщения (температура кипения)

Начальное состояние воды в цилиндре характеризуется давлением p₁ = F/S, Н/м², температурой T₁ (точка 1 на диаграммах p-v и p-T ). При подводе тепла Q вода сначала нагревается до температуры кипения (T_s) при p₁ = const, затем в процессе кипения при T_s = const и p₁ = const преобразуется в пар, который при дальнейшем подводе тепла нагревается до температуры T >T_s.

Обозначения на диаграммах:

1- состояние воды, недогретой до температуры кипения; b¢(B)-кипящая вода (T = T_s, p = p₁);

b’' (B) - сухой насыщенный пар (T = T_s, p = p₁).

Сухой насыщенный пар имеет температуру, равную температуре насыщения (T_s) при данном давлении.

Мокрый пар - точки b(B) на диаграммах - это смесь кипящей жидкости и сухого насыщенного пара.

Перегретый пар - точки d(D) на диаграммах - имеет температуру выше, чем температура насыщения при данном давлении (T>T_s).

Процесс парообразования (b¢- b¢¢ в p-v- диаграмме) - является изобарно-изотермическим процессом (p₁ = const и T_s = const), в котором кипящая вода преобразуется в сухой насыщенный пар (испарение).

Обратный процесс-переход пара в кипящую жидкость называется конденсацией, также является изобарно-изотермическим процессом.

В этих процессах давление и температура взаимосвязаны (T_s = f(p),
p_s = f(T)), данная связь на p–T- диаграмме представлена линией парообразования 1,согласно которой с возрастанием давления (p) температура насыщения (T_s) увеличивается.

Таким образом, состояния недогретой до температуры кипения воды и перегретого пара характеризуются двумя независимыми термическими параметрами, например, p и T; состояния кипящей воды, мокрого пара, сухого насыщенного пара - одним термическим параметром p или T.

Тройная точка (состояние А) - это одновременное существование твердой, жидкой и паровой фаз. Параметры тройной точки для воды:
p_A = 611 Па, t_A = 0,01 ⁰С, v_A = 0,001 м³/кг.

Критическая точка (состояние К) - это одновременное существование жидкой и паровой фаз. Для воды параметры критической точки: p_kp = 221,15 бар, t_kp = 374,12 ⁰С, v_kp = 0,003147 м³/кг.

Итак, вода и водяной пар могут находиться в пяти состояниях:

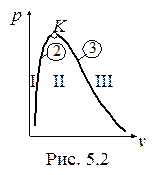1. Недогретая до температуры кипения вода (область I, рис. 5.2). Параметры обозначаются следующим образом: p, T, v, h, u, s.

2. Кипящая вода (нижняя пограничная кривая 2). Параметры обозначаются так: p, T_s, v¢, h¢, u¢, s¢ или так: T, p_s, v¢, h¢, u¢, s.¢

3. Мокрый пар (область II). Параметры обозначаются таким образом: p, T_s, v, h, u, s или p_s T, v, h, u, s.

4. Сухой насыщенный пар (верхняя пограничная кривая 3). Параметры обозначаются следующим образом: p, T_s, v¢¢, h¢¢, u¢¢, s¢¢ или T, p_s, v¢¢, h¢¢, u¢¢, s¢¢.

5. Перегретый пар (область III). Параметры обозначаются так:

p, T, v, h, u, s.

Выше критической точки (К) находится область однофазных состояний, в которой нельзя провести четкой границы между жидкостью и паром.