Тема: Маршруты, циклы, связность.

Задание №1

По заданной матрице смежности определить число маршрутов длины 3 между любой парой вершин в графе:

	A	B	C	D
A
B
C
D

Восстановить маршрут из вершины С в вершину А.

Решение:

Вычислим последовательно степени матрицы S.

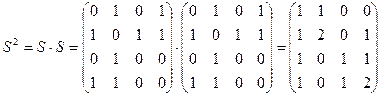
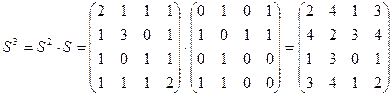
Из полученной матрицы S³ следует, что имеется два (A-A)-маршрута длины 3, четыре (B-A)-маршрута длины 3, один (C-A)-маршрут длины 3, три (D-A)-маршрута длины 3, т.е. число в (i, j) ячейке определяет количество маршрутов длины 3 из i-ой вершины в j-ую вершину.

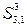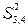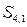Восстановим (C-A)-маршрут: элемент , равный единице, был получен в результате умножения элементов и , в свою очередь элемент 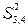получился путем умножения 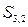и 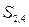. Тем самым, в формировании элемента 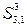участвовали элементы 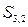, 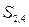и 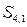матрицы смежности, поэтому (C-A)-маршрут есть последовательность вершин (C, B, D, A).

Задание №2

По заданной матрице определить сильные компоненты связности графа:

	A	B	C	D	E
A
B
C
D
E

Решение:

Максимальная степень, в которую надо возвести матрицу смежность для определения сильных компонент связности равна диаметру графа. Для данного графа диаметр равен 3. Возведём матрицу смежности в 3 степень:

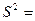
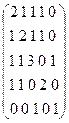
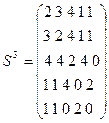
Компоненте сильной связности в матрице достижимости соответствует подматрица максимального размера, каждый элемент которой не равен 0. В данной матрице можно выделить три подматрицы: 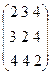, (2), (2).

Это значит, что граф, описанный матрицей смежности имеет три сильные компоненты: {A, B, C}, {D}, {E}.

Задания для самостоятельного решения:

Задание №1

По заданной матрице смежности определить число маршрутов длины 3 между любой парой вершин в графе.

Задание №2

По заданной матрице определить сильные компоненты связности графа

Варианты заданий:

Вариант №1   A B C D E A B C D E	Вариант №2   A B C D E A B C D E
Вариант №3   A B C D E A B C D E	Вариант №4   A B C D E A B C D E
Вариант №5   A B C D E A B C D E	Вариант №6   A B C D E A B C D E
Вариант №7   A B C D E A B C D E	Вариант №8   A B C D E A B C D E
Вариант №8   A B C D E A B C D E	Вариант №10   A B C D E A B C D E
Вариант №9   A B C D E A B C D E	Вариант №12   A B C D E A B C D E
Вариант №11   A B C D E A B C D E	Вариант №14   A B C D E A B C D E

Вариант №15   A B C D E A B C D E	Вариант №16   A B C D E A B C D E
Вариант №17   A B C D E A B C D E	Вариант №18   A B C D E A B C D E
Вариант №19   A B C D E A B C D E	Вариант №20   A B C D E A B C D E