Общий алгоритм статического расчета МКЭ

В принципе общий алгоритм расчета МКЭ сводится к последовательности шагов (матричных операций), в результате выполнения которых определяются необходимые параметры решения задачи (перемещения, деформации, напряжения). На практике расчеты по МКЭ всегда выполняются с применением компьютерных технологий, реализующих известные матричные формулы и выражения для получения промежуточных и конечных результатов.

Ниже приведены основные этапы статического расчета конструкции МКЭ.

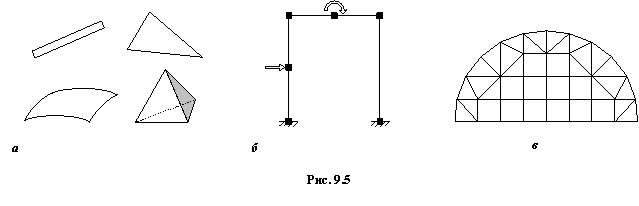
1.Дискретизация конструкции. Рассматриваемая область представляется в виде совокупности конечных элементов, соединенных между собой в узловых точках. Сами элементы могут иметь различную форму и размеры, например, в виде стержня, треугольной пластинки, прямоугольной в плане оболочки, пространственного тетраэдра (рис. 9.5, а). Выбор типа КЭ и общего их числа зависит от вида и формы конструкции, от требуемой точности, от характера внешней нагрузки и наложенных связей. Например, при расчете стержневых систем каждый стержень постоянного сечения принимается за отдельный элемент (рис. 9.5, б). Решение в этом случае получается точным.

Дискретизация континуальных систем (пластины, оболочки, массивы) является более сложной задачей. Общих рекомендаций по нанесению сетки или разбивке области на отдельные элементы нет. Обычно руководствуются предварительными представлениями о характере ожидаемого результата и в местах предполагаемых высоких градиентов искомых величин сетку КЭ сгущают. Однако следует помнить, что применение неравномерной разбивки может вызвать дополнительные трудности, связанные с ухудшением обусловленности системы разрешающих уравнений. Вообще рациональная разбивка требует некоторых практических навыков. Она может быть самой разнообразной. При решении двумерных задач (балка-стенка, изгиб плиты) дискретизация области обычно производится треугольными и прямоугольными элементами (рис. 9.5, в). Предполагается, что вся действующая нагрузка приводится к узловой, поэтому, например, в случае распределенной нагрузки для ее более точного моделирования бывает необходимо вводить дополнительные узлы и элементы. Заданные перемещения, жесткие или упругие связи также должны быть отнесены к узлам.

Таким образом, первый этап заключается в составлении конечно-элементной схемы – дискретной модели конструкции. Здесь можно выделить следующие действия:

а) выбор типа КЭ (по геометрии, виду аппроксимации и т. п.);

б) разбивку области на КЭ (с нумерацией узлов и элементов);

в) описание каждого элемента: топологические (номера узлов в сетке), физико-механические (модуль упругости и т. п.), геометрические характеристики;

г) описание каждого узла (координаты в общей системе координат);

д) описание заданных узловых нагрузок и перемещений.

Несмотря на то, что перечисленные выше действия не опираются на строгие теоретические рекомендации и во многом выполняются интуитивно, первый этап имеет большое значение для дальнейшего расчета конструкции.

2. Построение глобальных матрицы жесткости и вектора узловых сил. Процедура основана на формировании МЖ и ВН отдельных элементов и их размещении в глобальных МЖ и ВН путем обхода по всем конечным элементам дискретной модели.

Расчеты по МКЭ различных конструкций отличаются принципиально только применяемыми элементными МЖ, ВН и матричными операторами для определения внутренних усилий и напряжений. Данные матрицы и векторы строятся на основе вариационных принципов с учетом принятой геометрии КЭ и выбранных аппроксимаций. В случае если МЖ и ВН конечного элемента построены в локальной (местной) системе координат, не совпадающей с глобальной, необходимо преобразовать их для глобальной системы.

Размещение элементных МЖ (ВН) в глобальной МЖ (ВН) может быть выполнено одним из следующих способов:

1) непосредственного сложения жесткостей;

2) конгруэнтного преобразования;

3) при помощи конечно-разностных операторов.

Способ непосредственного сложения жесткостей, используемый в большинстве случаев, реализуется следующим образом:

– МЖ отдельного элемента представляется в блочной форме, где число блоков (в строке или в столбце) определяется количеством узлов КЭ, размерность каждого блока соответствует числу степеней свободы в узле;

– каждая строка или столбец блочной МЖ элемента соответствует глобальному номеру узла в конечно-элементной модели конструкции;

– глобальная МЖ также представляется в виде блоков, аналогично элементной, число блоков соответствует общему числу узлов дискретной модели;

– МЖ каждого элемента размещается поблочно в глобальной МЖ согласно адресам блоков, т. е. глобальным номерам узлов.

На рис. 9.6 изображена схема размещения МЖ треугольного элемента (три узла, две степени свободы в узле) в глобальной МЖ. Здесь 1, 2, 3 – локальные номера узлов в элементе, i, j, k – глобальные номера узлов.

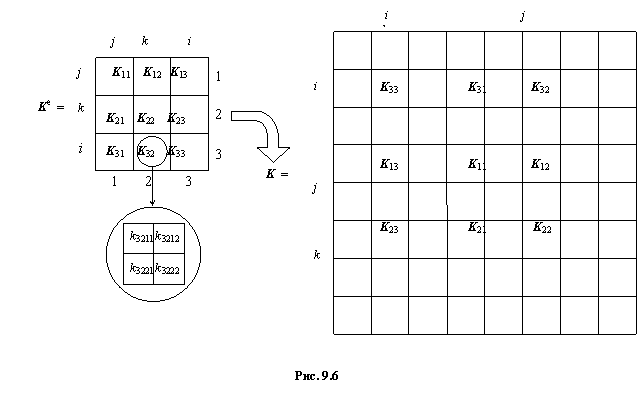По аналогичной схеме из элементных ВН формируется глобальный ВН для всей конструкции.

Таким образом, данный этап включает следующие основные действия, выполняемые в цикле для каждого из конечных элементов:

а) составление элементных МЖ и ВН в локальной системе координат;

б) преобразование элементных МЖ и ВН из локальной в глобальную систему координат – в том случае, если локальная система не совпадает с глобальной;

в) размещение элементных МЖ и ВН в глобальных МЖ и ВН.

Сформированная на этом этапе МЖ системы является вырожденной или особенной. Она может быть преобразована в невырожденную при учете кинематических граничных условий (внешних связей, наложенных на некоторые узлы и исключающих перемещение конструкции как абсолютно твердого тела).

3. Учет заданных граничных условий. Пусть в результате выполнения второго этапа система разрешающих уравнений имеет вид

K q = P, (9.1)

где глобальная матрица жесткости K содержит коэффициенты k_ij; вектор узловых перемещений q – компоненты перемещений q_i; вектор узловой нагрузки P – узловые силы p_i. (i = 1, …, n; j = 1, …, n; n – число степеней свободы системы).

Статические граничные условия учитываются при формировании вектора нагрузки P. Проблема решается просто, если внешние нагрузки заданы непосредственно в узловых точках. Распределенные же нагрузки заменяются эквивалентными обобщенными узловыми силами P_узл, при этом с целью уменьшения погрешности расчета часто приходится разбивать конструкцию на более мелкие элементы. Эти узловые силы добавляются к тем, что получены при формировании (на 2-м этапе) вектора P из элементных нагрузок P_эл:

P_l = P_{l эл} + P_{l узл}; (l = 1, … , n_p),

где n_p – число компонент узловой нагрузки.

Кинематические граничные условия, как правило, представляются в виде заданных узловых перемещений (равных и не равных нулю). Нулевые перемещения соответствуют абсолютно жестким опорным связям, наложенным на некоторые узлы дискретной модели конструкции. Отличные от нуля заданные перемещения могут быть обусловлены неточностью изготовления (монтажа), регулированием усилий, смещением (осадкой) опор и т. п.

Пусть q_m – заданное перемещение по направлению m-й степени свободы (m = 1, … , n_q). Тогда корректировка системы уравнений (9.1) может быть произведена следующим образом (в цикле по всем компонентам заданных узловых перемещений n_q):

1) из вектора P вычитается m-й столбец матрицы K, умноженный на q_m:

p_i = p_i – k_im q_m, (i = 1, … , n);

2) обнуляются m-я строка и m-й столбец матрицы K:

k_im = 0; k_mi = 0, (i = 1, … , n);

3) m-й коэффициент главной диагонали принимается равным единице: k_mm = 1;

4) m-ю компоненту вектора P следует положить равной q_m, т. е. p_m = q_m.

Если заданное перемещение q_m 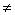0, то выполняются все перечисленные пункты, если q_m = 0 – выполняются только 2, 3 и 4-й пункты. Во втором случае также можно вычеркнуть m-ю строку и m-й столбец из матрицы K и m-ю компоненту из векторов P и q, тем самым уменьшив размерность системы алгебраических уравнений МКЭ на число компонент заданных смещений – n_q.

Помимо жестких связей и смещений опор в реальной конструкции могут иметь место упругие связи (упругое основание). Наиболее простой является дискретная модель основания, когда упругие связи приложены в отдельных узлах. В этом случае к МЖ всей системы просто добавляется диагональная матрица, состоящая из коэффициентов жесткости упругих связей:

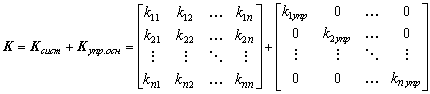. (9.2)

Учет распределенного упругого основания будет более точным, если при его дискретизации использовать вариационные принципы (например, принцип Лагранжа). При таком подходе для каждого конечного элемента, подобно МЖ, строится так называемая матрица реакций основания. Последняя добавляется к МЖ элемента, и далее расчет производится в обычном порядке.

Последовательность действий при учете заданных граничных условий:

а) замена произвольной внешней нагрузки на эквивалентные узловые силы и добавление их в глобальный ВН;

б) дополнение МЖ при учете заданного упругого основания;

в) корректировка глобальной системы уравнений (МЖ и ВН) при учете заданных ненулевых смещений узлов;

г) преобразование глобальной системы уравнений при учете жестких опорных связей (нулевых перемещений).

В результате учета граничных условий глобальная система разрешающих уравнений будет сформирована в окончательном и в то же время достаточном для получения искомого решения виде.

4. Решение системы разрешающих уравнений. Окончательная система разрешающих уравнений МКЭ для статической задачи представляет собой систему линейных алгебраических уравнений с симметричной, положительно определенной матрицей коэффициентов, как правило, ленточной структуры.

Прежде всего следует выбрать метод решения СЛАУ. Для небольших и средних задач – от несколько десятков до несколько десятков тысяч неизвестных – обычно используются известные прямые методы: Гаусса, разложения Холесского, LDL^T–факторизации и т. п. Для более сложных систем, требующих огромного объема вычислений и значительной памяти, приходится искать и, если необходимо, создавать специально подходящие для данной задачи эффективные алгоритмы, основанные как на прямых, так и на итерационных методах. Помимо перечисленных, для решения систем разрешающих уравнений МКЭ эффективны такие прямые методы, как метод быстрого преобразования Фурье, методы Гивенса, Хаусхолдера, блочного разложения. В ряде случаев целесообразно применять методы, учитывающие разреженность матриц, а также плохую обусловленность систем уравнений.

Касаясь итерационных методов, отметим следующее. Классические из них – методы Якоби, Гаусса-Зейделя, несмотря на сравнительную простоту, при решении даже средних задач характеризуются крайне медленной сходимостью. Более эффективными (в которых при меньшем числе итераций достигается такая же точность решения) являются следующие итерационные методы: метод последовательной верхней релаксации (модификация процедуры Гаусса-Зейделя с ускорением сходимости), некоторые градиентные методы, в частности, сопряженный метод Ньютона, метод Шелдона, а также ряд блочных итерационных методов.

Можно применять и комбинированные подходы. Так, точность решения, полученного прямым методом, может быть значительно улучшена с помощью дополнительных вычислений, называемых итерационным уточнением.

Отметим некоторые особенности, присущие системе разрешающих уравнений МКЭ. Эти особенности могут значительно влиять на точность получаемого решения, объем вычислений и режим работы вычислительной техники.

Во-первых, при рациональной нумерации узлов матрица коэффициентов СЛАУ имеет ленточную структуру. Это означает, что ненулевые коэффициенты матрицы содержатся только в пределах некоторой полосы – ленты, занимающей диагональное положение в матрице (рис. 9.7).

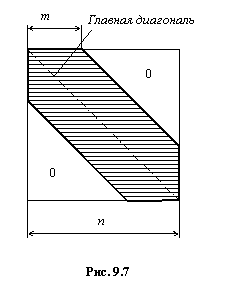
Внутри ленты могут находиться и нулевые коэффициенты. Важным моментом является то, что область нулевых элементов матрицы, расположенная выше и ниже ленты, остается нулевой и в процессе решения системы уравнений. Очевидно, что с уменьшением ширины ленты уменьшается и объем производимых вычислений. Ширина ленты определяется по формуле

m = (r_max +1) n_s.

Здесь r_max – величина наибольшей разности между глобальными номерами узлов в пределах каждого КЭ, определяемая при обходе по всем элементам системы; n_s – число степеней свободы узла. Для уменьшения ширины ленты следует стремиться к оптимальной нумерации узлов, при которой параметр r_max принимает минимальное значение. Пример разбивки двумерной области на прямоугольные элементы с разными вариантами нумерации узлов приведен на рис. 9.8. Рациональная нумерация узлов дает m = 10, а нерациональная – m = 16 (при n_s = 2).

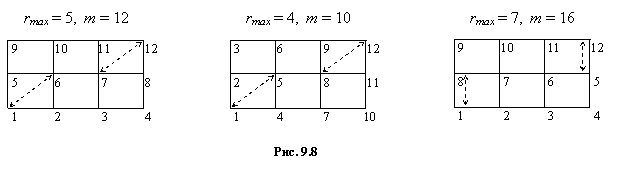
Во-вторых, при решении больших СЛАУ (свыше тысячи уравнений) важным фактором является значительное накопление ошибок округления, возникающих в процессе огромного количества арифметических операций.

Так, например, при использовании метода Гаусса число умножений примерно равно 1/3mn², где n – порядок системы, m – ширина «ленты». В этом случае уже при нескольких сот уравнений рекомендуется применять двойную точность вычислений (16 знаков после запятой), иначе следует считаться с неизбежной погрешностью получаемого решения.

Основная доля задач в строительстве (исключение составляют крупные сооружения, сложные и ответственные в инженерном плане конструкции и т. п.) относится к задачам средней технической сложности, для которых, как уже было сказано выше, используются прямые методы решения систем уравнений. К тому же при практических расчетах часто бывает необходимо учитывать различные виды нагрузок, к примеру, собственный вес, временную нагрузку от кранового и другого оборудования, снеговую и ветровую нагрузки и т. д. Решение системы уравнений по каждому виду загружения также удобнее всего выполнять с помощью прямых методов. Такое утверждение основывается на том, что любой из прямых методов можно представить в виде двух независимых процедур:

а) приведения матрицы коэффициентов СЛАУ к треугольному виду посредством последовательных исключений или же факторизацией (разложением исходной матрицы на несколько треугольных);

б) решения систем с треугольными матрицами коэффициентов для каждого вектора нагрузки – вида загружения.

5.Определение внутренних усилий (напряжений). Результатом решения системы разрешающих уравнений МКЭ в форме метода перемещений будут компоненты узловых перемещений дискретной модели конструкции.

Вычисление же необходимых компонент напряженного состояния конструкции производится поэлементно в следующем порядке:

а) формируется вектор узловых перемещений для каждого конечного элемента q^e (посредством выборки из глобального вектора узловых перемещений q соответствующих компонент);

б) если локальная система координат для отдельного КЭ не совпадает с глобальной, производится преобразование вектора узловых перемещений q^e данного элемента;

в) на основе геометрических и физических соотношений формируется матрица усилий (напряжений) для КЭ – G;

г) вычисляется вектор узловых значений внутренних усилий (напряжений) для КЭ – S ^e, который связан с узловыми перемещениями в общем случае следующим соотношением:

S ^e = G q ^e.

Основные этапы статического расчета конструкций МКЭ и последовательность их выполнения приведены в виде схемы на рис. 9.9.

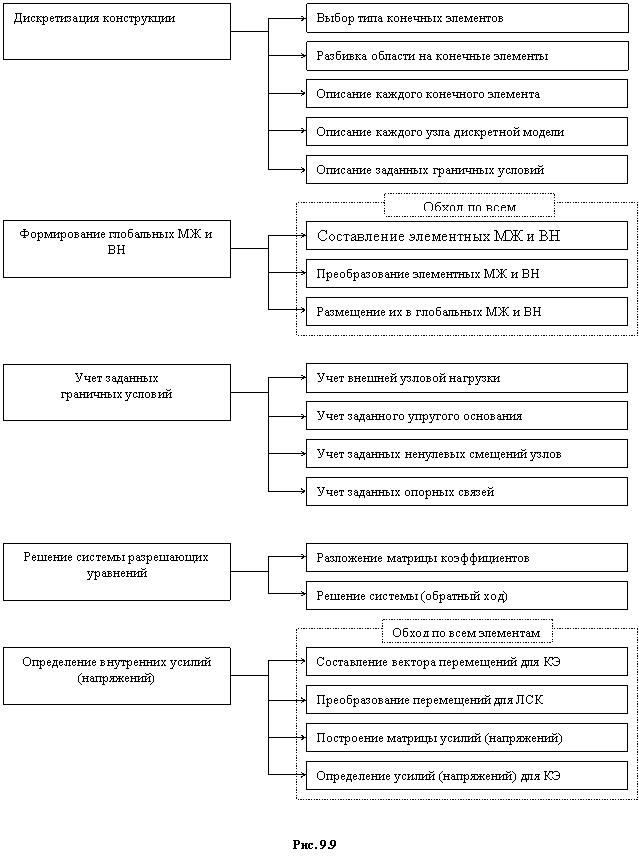Литература

1. Васильева В.Н. Введение в теорию метода конечных элементов. - Иркутск, 1986.

2. Зенкевич О. (O.C. Zienkiewicz), Морган К. (K. Morgan) Конечные элементы и аппроксимация: Пер. с англ. - М.: Мир, 1986.

3. Интернет, www.stroitmeh.ru/lect31.htm