Тема: «Множества и операции над ними»

I ВАРИАНТ

1. Изобразите при помощи кругов Эйлера отношения между множествами А и В, если

1) А - множество чётных чисел;

В - множество чисел кратных 5;

2) А - множество квадратов;

В - множество прямоугольников с равными сторонами;

2.. Найдите пересечение множеств А и В, если:

1)А={а,Ь, с, d, е} В = {k, m, d, t, f)

2) А = {17, 20, 21, 22, 30} В = {19, 22, 25, 26, 27}

3. Изобразите в прямоугольной системе координат множества,
если а) х = {- 2, - 1, 0, 1, 2}, у⁼ {1, 2}

б) ,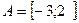

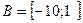
4. Дано: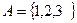

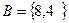
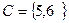
Составить множество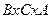

5. Найдите пересечение и объединение множеств: -4 <Х <3 и 1 <Х <9

6. В группе туристов, состоящей из 100 человек, 10 человек не знали ни немецкий, ни французский языки, 75 знали немец­кий, 83 знали французский. Сколько туристов знали два языка?

II ВАРИАНТ

1. Изобразите при помощи кругов Эйлера отношения межу множествами А и В, если:

1) А - множество чисел, кратных 3;
В - множество чисел, кратных 6;

2) А - множество нечётных чисел;
В - множество чисел, кратных 4;

2. Найдите объединение множеств А и В, если:

1) А= { а, о, и, у, ю} В = {а, б, и, к, о}

2) А = {3, 6, 9, 12, 15} В = {6, 1, 2, 5, 9, 13}

3)

3. Изобразите в прямоугольной системе координат множество, если:

а) х = {3, 4, 5, 6} у = [- 2, 2]

б)х = [1,3] У=[2,5]

4. Дано: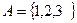

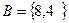
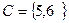
Составить множество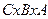

5. Найдите пересечение и объединение множеств: -6 <Х <2 и 1 <Х <5

6. Из 38 учащихся класса 24 занимаются в хоре и 15 в лыж­ной секции. Сколько учащихся занимается и в хоре, и в лыж­ной секции, если в классе нет учащихся, не посещающих заня­тий хора или лыжной секции?

Раздел IV. Понятие текстовой задачи и процесса ее решения

Тема 4.1. Понятие текстовой задачи. Способы и этапы ее решения

План лекции:

1. Понятие текстовой задачи, ее структура.

2. Методы решения текстовых задач.

3. Этапы решения задач и приемы их выполнения.

1. Задача является средством формирования умений строить математические модели реальных явлений, а также средством развития мышления.

Поэтому надо знать, как построены задачи и уметь их решать прежде всего арифметическим способом.

Структура текстовой задачи.

Простая задача – словесная модель явления (ситуации).

Пример: Свитер, шапку и шарф связали из 1200г шерсти. На шарф потребовалось на 100г шерсти больше, чем на шапку и на 400г меньше, чем на свитер. Сколько шерсти израсходовали на каждую вещь?

Свитер, шапка и шарф – объекты задачи.

Относительно этих объектов имеются определенные утверждения и требования.

Утверждения: (условие)

1. Свитер, шапка и шарф связаны из 1200 г шерсти.

2. На шарф израсходовали на 100 г больше, чем на шапку.

3. На шарф израсходовали на 400г меньше, чем на свитер.

Требования:

1. Сколько израсходовали на свитер?

2. Сколько израсходовали на шапку?

3. Сколько израсходовали на шарф?

Решением задачи называется процесс нахождения результата.

2. Методы решения текстовых задач:

Арифметический метод.

Решить задачу арифметическим методом, значит найти ответ на требование задачи посредством выполнения арифметических действий над числами.

Одну и ту же задачу можно решить различными арифметическими способами.

Пример: Сшили 3 платья, расходуя на каждое по 4 м ткани. Сколько блузок можно было сшить из этой ткани, если расходовать на одну 2 м?

1 способ.

1) 4*3=12 (м) – было ткани

2) 12:2=6 (блузок) – можно сшить из12 м ткани

2 способ.

1) 4:2 = 2 (раза) – во столько раз больше идет на платье, чем на блузку

2) 3*2=6 (блузок) – столько блузок можно сшить из ткани