Теорема. Для с.к.-непрерывности СП в точке необходимо и достаточно, чтобы матожидание было непрерывно в , а корреляционная функция непрерывна в точке .

Из теоремы сразу следует, что 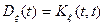должна быть непрерывной.

Чтобы исследовать с.к.-непрерывность СП достаточно исследовать непрерывность ее моментных характеристик.

Пример. Пуассоновский процесс.

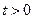Пуассоновский процесс имеет следующий физический смысл: при всяком величина численно равна количеству событий из простейшего потока интенсивности 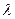, произошедших к моменту времени .

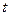При каждом 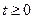сечение имеет распределение Пуассона с параметром :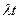

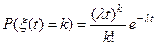
СП сходится по вероятности 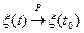, но реализации разрывны. Это происходит потому, что разрывы на каждой реализации в своих точках, и вероятность того, что разрыв будет именно в данной точке 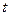равна 0.

Дифференцируемость СП

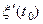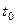СВ называется с.к.-производной СП в точке , если выполняется

.

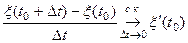Если предел существует, то является с.к.-дифференцируемым в точке 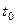. Если дифференцируем в каждой точке 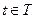, то говорят, что с.к.-дифференцируем на интервале 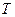, а семейство СВ 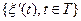называется с.к.-производной СП на .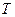

Теорема. Критерий с.к.-дифференцируемости.

Для того чтобы СП был с.к.-дифференцируем в точке , необходимо, чтобы существовали производные и , и достаточно, чтобы эти производные были непрерывны в точках и соответственно.

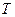Если СП дифференцируем на , то его с.к.-производная 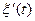имеет матожидание и корреляционную функцию, определяемые как

И .

СП называется дифференцируемым потраекторно на 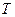, если почти все его траектории - дифференцируемые функции, т.е.

.

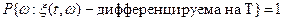Если 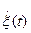потраекторная производная СП , а 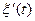- с.к.-производная ,то 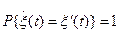, т.е. СП 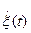и 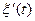являются стохастически эквивалентными.

Пример.

СП: 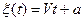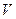- СВ с равномерным распределением на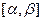

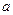- неслучайная величина.

Определить, имеет ли СП с.к.-производную.

,

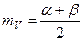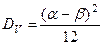
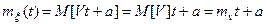
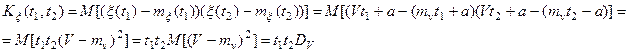Определим, имеет ли этот процесс с.к.-производную (выполняются ли условия теоремы).

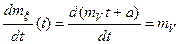
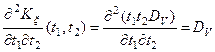
Производные существуют и непрерывны в каждой точке.

Интегрирование СП

Понятие интеграла от случайного процесса также будем изучать в двух вариантах: с.к.-интеграл и потраекторный интеграл.

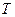Пусть СП на . На 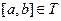возьмем некоторое разбиение 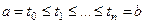, а на каждом из промежутков выберем произвольную точку .

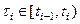Если существует предел в с.к.-смысле

,

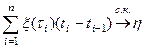не зависящий от способа разбиения и выбора точек 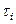, то СП называется с.к.-интегрируемым на 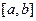, а случайная величина 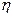называется с.к.-интегралом:

.

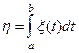Теорема. Критерий с.к.-интегрируемости.

Для существованияс.к.-интеграла 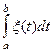необходимо и достаточно, чтобы существовали следующие интегралы Римана:

, .

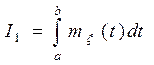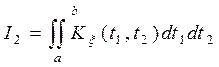Всякий процесс с.к.-непрерывный на 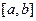является с.к.-интегрируемым на .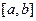