Сложение гармонических колебаний, направленных вдоль одной прямой
Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
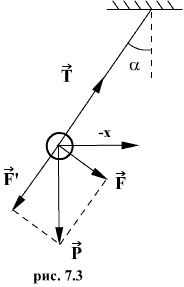
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 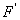 , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 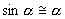 и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
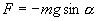
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
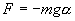
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 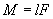 , и момент инерции:
, и момент инерции: 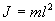
Угловое ускорение:
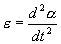
С учетом этих величин имеем:
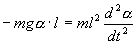
или
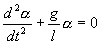 | (7.8) |
Его решение
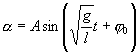 ,
,
где 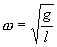 и и 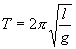 | (7.9) |
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
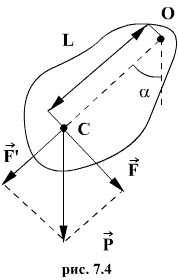
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
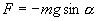
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
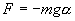
Применив основное уравнение динамики вращательного движения, выведем закон движения математического и физического маятников. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
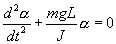 | (7.10) |
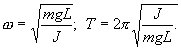 | (7.11) |
Решение этого уравнения
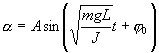
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 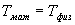 или
или
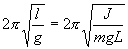 .
.
Из этого соотношения определяем
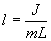
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
7.6. Сложение механических колебаний
Сложение гармонических колебаний, направленных вдоль одной прямой.
Рассмотрим сложение одинаково направленных колебаний одного периода, но отличающихся начальной фазой и амплитудой. Уравнения складываемых колебаний заданы в следующем виде:
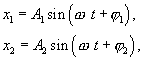
где 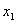 и
и 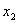 - смещения;
- смещения; 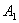 и
и 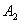 - амплитуды;
- амплитуды; 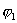 и
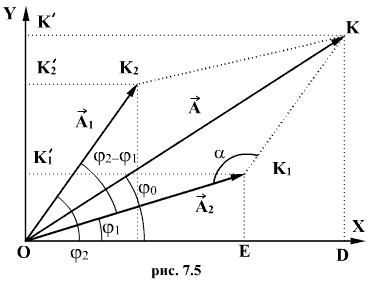
и 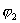 - начальные фазы складываемых колебаний. Амплитуду результирующего колебания удобно определить с помощью векторной диаграммы (рис. 7.5), на которой отложены векторы амплитуд
- начальные фазы складываемых колебаний. Амплитуду результирующего колебания удобно определить с помощью векторной диаграммы (рис. 7.5), на которой отложены векторы амплитуд 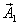 и
и 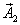 складываемых колебаний под углами
складываемых колебаний под углами 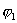 и
и 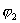 к оси х и по правилу параллелограмма получен вектор амплитуды суммарного колебания
к оси х и по правилу параллелограмма получен вектор амплитуды суммарного колебания 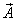 . Если равномерно вращать систему векторов (параллелограмм) и проектировать векторы на ось OY, то их проекции будут совершать гармонические колебания в соответствии с заданными уравнениями. Взаимное расположение векторов
. Если равномерно вращать систему векторов (параллелограмм) и проектировать векторы на ось OY, то их проекции будут совершать гармонические колебания в соответствии с заданными уравнениями. Взаимное расположение векторов 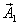 , и
, и 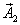 при этом остается неизменным, поэтому колебательное движение проекции результирующего вектора
при этом остается неизменным, поэтому колебательное движение проекции результирующего вектора 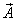 тоже будет гармоническим.
тоже будет гармоническим.
Отсюда следует вывод, что суммарное движение - гармоническое колебание, имеющее заданную циклическую частоту. Определим модуль амплитуды А результирующего колебания В 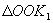 угол
угол 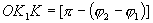 (из равенства противоположных углов параллелограмма).
(из равенства противоположных углов параллелограмма).
Следовательно
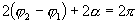
отсюда
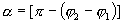 .
.
Согласно теореме косинусов
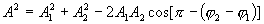
или
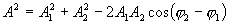 | (7.12) |
Начальная фаза 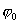 результирующего колебания определяется из
результирующего колебания определяется из 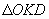 :
:
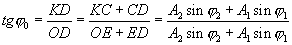
Соотношения для фазы и амплитуды позволяют найти амплитуду и начальную фазу результирующего движения и составить его уравнение
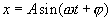
Биения
Рассмотрим случай, когда частоты двух складываемых колебаний мало отличаются друг от друга 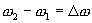 , и пусть амплитуды одинаковы и начальные фазы
, и пусть амплитуды одинаковы и начальные фазы 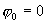 , т.е.
, т.е.
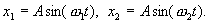
Сложим эти уравнения аналитически
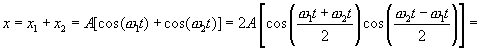
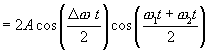
Преобразуем
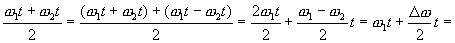
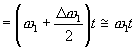
Тогда
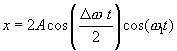
Так как 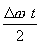 все же медленно изменяется, величину
все же медленно изменяется, величину 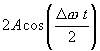 нельзя назвать амплитудой в полном смысле этого слова (амплитуда величина постоянная). Условно эту величину можно назвать переменной амплитудой. График таких колебаний показан на рис. 1.6 Складываемые колебания имеют одинаковые амплитуды, но различны периоды, при этом периоды
нельзя назвать амплитудой в полном смысле этого слова (амплитуда величина постоянная). Условно эту величину можно назвать переменной амплитудой. График таких колебаний показан на рис. 1.6 Складываемые колебания имеют одинаковые амплитуды, но различны периоды, при этом периоды 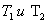 отличаются незначительно друг от друга. При сложении таких колебаний наблюдаются биения. Число n биений в секунду определяется разностью частот складываемых колебаний, т.е.
отличаются незначительно друг от друга. При сложении таких колебаний наблюдаются биения. Число n биений в секунду определяется разностью частот складываемых колебаний, т.е.
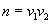
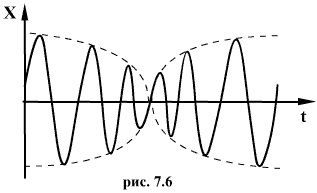
Биения можно наблюдать при звучании двух камертонов, если частоты и колебаний близки друг к другу.
