Задача выпуклого программирования
Если в задаче математического программирования требуется найти экстремум функции, например:
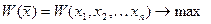 (4.7)
(4.7)
на множестве допустимых решений, заданных ограничениями
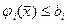 ,
, 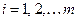 (4.8)
(4.8)
причем:
1) целевая функция 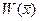 является дифференцируемой и вогнутой, т.е. для нее выполняется условие:
является дифференцируемой и вогнутой, т.е. для нее выполняется условие:
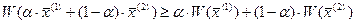 при любых
при любых 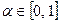 ,
,
2) а левые части всех ограничений 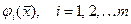 — дифференцируемыми и выпуклыми функциями, т.е. для них выполняются условия:
— дифференцируемыми и выпуклыми функциями, т.е. для них выполняются условия:
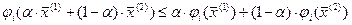 при любых
при любых 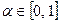 ,
,
Тогда задача (4.7)-(4.8) называется задачей выпуклого программирования.
Любая линейная функция одновременно удовлетворяет условиям и выпуклости, и вогнутости; т.е. её можно считать как выпуклой, так и вогнутой. Это позволяет считать линейные задачи частным случаем задач выпуклого программирования.
Если для задач математического программирования в общем случае пока отсутствует стройная теория существования и устойчивости решения, то для задач выпуклого программирования такая теория есть.
Введём три определения:
1). Функцией Лагранжа задачи выпуклого программирования (4.7)-(4.8) называется функция:
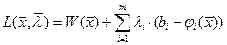 ,
,
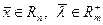 , (4.9)
, (4.9)
2). Говорят, что задача выпуклого программирования (4.7)-(4.8) удовлетворяет условию регулярности, если существует хотя бы одна внутренняя точка множества допустимых решений 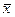 , определяемого строгими неравенствами, полученными из (4.8) (т.е.
, определяемого строгими неравенствами, полученными из (4.8) (т.е. 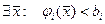 ).
).
3). Точка 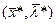 называется седловой точкой функции
называется седловой точкой функции 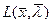 , если для всех
, если для всех 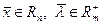 выполнено:
выполнено:
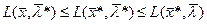 (4.10)
(4.10)
Если целевая функция (убрать)
В теории нелинейного программирования центральное место занимает теорема Куна-Таккера, обобщающая классический метод множителей Лагранжа на случай, когда ограничения нелинейной задачи наряду с ограничениями в виде равенств содержат также и ограничения в виде неравенств.
Теорема Куна-Таккера. Если задача выпуклого программирования (4.7)-(4.8) удовлетворяет условию регулярности, то точка 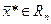 является оптимальным решением этой задачи тогда и только тогда, когда существует такая точка
является оптимальным решением этой задачи тогда и только тогда, когда существует такая точка 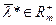 с неотрицательными координатами, что
с неотрицательными координатами, что 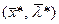 является седловой точкой функции Лагранжа данной задачи.
является седловой точкой функции Лагранжа данной задачи.
Условия Каруша-Куна-Таккера в дифференциальной форме:
Если функция Лагранжа 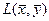 является выпуклой по
является выпуклой по 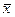 , вогнутой по
, вогнутой по 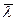 и непрерывно дифференцируемой по всем
и непрерывно дифференцируемой по всем 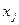
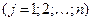 и
и 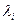
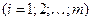 , то для того чтобы пара
, то для того чтобы пара 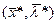 была седловой точкой функции Лагранжа
была седловой точкой функции Лагранжа 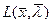 , необходимо и достаточно, чтобы выполнялись следующие условия:
, необходимо и достаточно, чтобы выполнялись следующие условия:
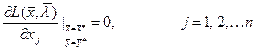 ,
,
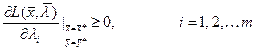 ,
,
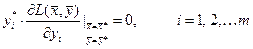 ,
,

Пример.
Найти максимум функции 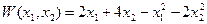
на множестве допустимых решений 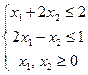 .
.
Решение:
Функция 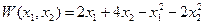 является вогнутой, система ограничений содержит только линейные неравенства, поэтому задача является задачей выпуклого программирования.
является вогнутой, система ограничений содержит только линейные неравенства, поэтому задача является задачей выпуклого программирования.
Составим функцию Лагранжа
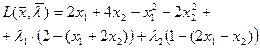
Найдём седловую точку функции Лагранжа из условий:
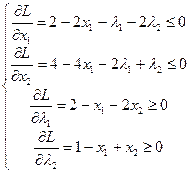 .
.
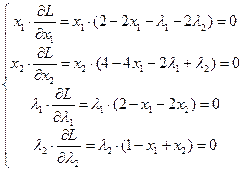
В данном случае седловой точкой является пара 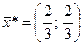 ,
, 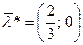 .
.
Ответ: 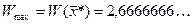
Теорема Куна-Таккера обосновывает сведение задачи выпуклого программирования к задаче поиска седловой точки функции Лагранжа. Чтобы такое сведение имело практический смысл, необходимо, чтобы получившаяся задача была в чём-то проще исходной. Это происходит не всегда, поэтому разработан ряд прямых методов поиска решения нелинейной задачи (4.5), (4.6). Рассмотрим некоторые из них.
