Системы линейных уравнений. Сибирский государственный университет телекоммуникаций
Сибирский государственный университет телекоммуникаций
И информатики
Кафедра высшей математики
В.И. Агульник, Б.П. Зеленцов
ВЫСШАЯ МАТЕМАТИКА
Формулы, таблицы, графики
Справочное пособие
Новосибирск
2000 г.
В.И. Агульник, Б.П. Зеленцов.
Высшая математика. Формулы, таблицы, графики.
Справочное пособие.
Аннотация
Справочное пособие содержит формулы, таблицы, графики, охватывающие основные разделы высшей математики – линейной алгебры, аналитической геометрии, математического анализа. Оно предназначено для студентов 1 и 2 курса всех факультетов, при освоении теоретического материала, на практических занятиях и при выполнении домашних заданий по высшей математике. Пособие может быть также полезно студентам старших курсов при выполнении курсовых и дипломных работ.
Кафедра высшей математики
Рецензент: И.В.Перцев
Утверждено Редакционно-издательским Советом СибГУТИ в качестве учебного пособия.
© СибГУТИ, 2000.
© В.И. Агульник, Б.П. Зеленцов, 2000 г.
ОГЛАВЛЕНИЕ
1. ЛИНЕЙНАЯ АЛГЕБРА……………………………………………
2. ВЕКТОРНАЯ АЛГЕБРА………………………………………….
3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ………………………………
4. КОМПЛЕКСНЫЕ ЧИСЛА………………………………………...
5. ВВЕДЕНИЕ В АНАЛИЗ……………………………………………
6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ……………………….
7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ………………………………..
8. РЯДЫ………………………………………………………………..
9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ…………………………
10. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ……………………………….
11. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ……………………………….
12. ТЕОРИЯ ПОЛЯ……………………………………………………...
13. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ……….
14. ТЕОРИЯ ВЕРОЯТНОСТЕЙ………………………………………..
ЛИТЕРАТУРА………………………………………………………….
ЛИНЕЙНАЯ АЛГЕБРА.
1.1. Определители……………………………………………
1.2. Матрицы…………………………………………………
1.3. Системы линейных уравнений…………………………
Определители (детерминанты).
Обозначения определителя матрицы А: D, det A, 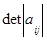
Определитель второго порядка: 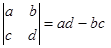 .
.
| Определитель третьего порядка: | 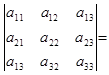 | 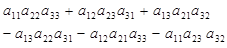 |
| Разложение определителя n-го порядка по i-й строке: | Разложение определителя n-го порядка по j-ому столбцу: |
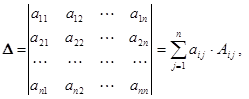 | 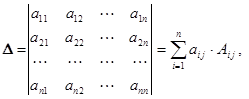 |
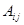 -алгебраическое дополнение элемента
-алгебраическое дополнение элемента 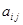 ,
, 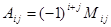 ,
,
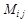 -минор, получаемый из определителя вычёркиванием i-й строки и j-го столбца.
-минор, получаемый из определителя вычёркиванием i-й строки и j-го столбца.
1.2. Матрицы 

| Матрица размерами n´m (n строк и m столбцов): | 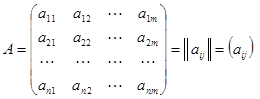 |
Равенство матриц: 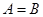 , если эти матрицы одного размера и
, если эти матрицы одного размера и 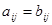 .
.
Сложение матриц: 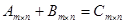 , где
, где 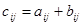 .
.
Умножение матрицы на число: 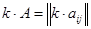 .
.
Транспонирование матрицы: 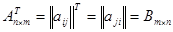
Умножение матриц: 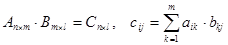
Обратная матрица: 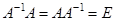 ,
, 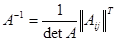 ,
,
где 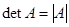 -определитель матрицы А .
-определитель матрицы А .
Виды матриц:
| единичная матрица: | 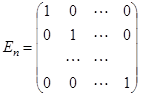 ; ; | симметрическая матрица: | 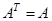 , , 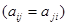 ; ; |
| матрица-строка: | 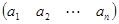 ; ; | матрица-столбец: | 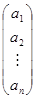 . . |
Ранг матрицы 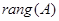 - порядок её наибольшего ненулевого минора или число линейно независимых строк (столбцов) матрицы.
- порядок её наибольшего ненулевого минора или число линейно независимых строк (столбцов) матрицы.
Системы линейных уравнений
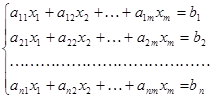 | 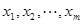 - неизвестные; aij –коэффициент в i-ом уравнении при j-ом неизвестном; - неизвестные; aij –коэффициент в i-ом уравнении при j-ом неизвестном; 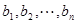 - свободные члены. - свободные члены. |
Матричный вид: 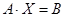 ,
, 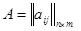 - матрица системы,
- матрица системы,
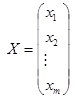 - столбец неизвестных,
- столбец неизвестных, 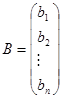 - столбец свободных членов.
- столбец свободных членов.
Совместность системы: 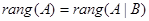
Формулы Крамера (n=m): 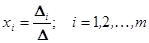 ,
,
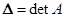 - определитель матрицы системы;
- определитель матрицы системы;
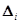 -определитель, полученный при замене i-го столбца матрица A на столбец В.
-определитель, полученный при замене i-го столбца матрица A на столбец В.
Однородная система (B=0):
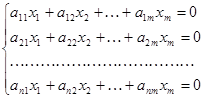 | Если 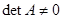 , то система имеет только нулевое решение , то система имеет только нулевое решение 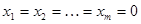 . Если . Если 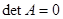 , то существуют ненулевые решения. , то существуют ненулевые решения. |
