Равновесной системы (правило фаз Гиббса)
1) Определение числа а:
а = 2 + (К-1)А,
где 2 – число интенсивных переменных Т и р, (К-1) – число независимых мольных долей N 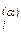 в каждой фазе α, А– число фаз α в системе.
в каждой фазе α, А– число фаз α в системе.
2) Определение числа в:
в = (А-1)К + R + L,
где (А-1) – число независимых уравнений связи из условия массового между фазами по каждому компоненту k, К – число компонентов k в системе, R – число независимых уравнений связи из условия химического равновесия между компонентами k (число базисных реакций в системе), L – число независимых уравнений связи из особых условий равновесия в конкретных системах.
3) Определение числа ω:
ω = а – в = 2 + (К-1)А - (А-1)К - R - L
 Алгебраические преобразования
Алгебраические преобразования
ω =2 + К – А – R – L – правило фаз Гиббса.
Выражение для расчета числа фаз, способных
К равновесному сосуществованию в системе.
ω =2 + К – А – R – L
 ω≥0 всегда
ω≥0 всегда
2 + К – А – R – L≥0
 Решение относительно А
Решение относительно А
А ≤ 2 + К – R – L.
Анализ однокомпонентных систем с помощью правила фаз Гиббса.
Общие соотношения.
1) К=1, R=0, L=0;
2) а =2 + (К-1)А=2 + (1-1)А = 2;
3) {Т, р, {N 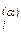 }
} 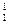 }={Т, р} (!);
}={Т, р} (!);
4) ω =2 + К – А – R – L= 2+1-А-0-0 = 3 – А;
5) А ≤ 2 + К – R – L= 2+1-0-0 = 3.
4.6.2. Однофазная система (А=1)
 ω = 3 – А = 3-1 = 2
ω = 3 – А = 3-1 = 2
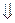 ω = а
ω = а
Из двух интенсивных переменных Т и р обе являются свободными.
 Изображение результата в пространстве Т – р
Изображение результата в пространстве Т – р
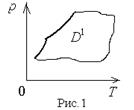
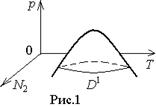
В пространстве Т – р для фазы α имеется некоторая область D 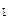 , где эта фаза
, где эта фаза
способна к равновесному существованию автономно (рис.1).
4.6.3. Двухфазная система (А=2).
 ω = 3 – А = 3-2 =1
ω = 3 – А = 3-2 =1
 ω< а
ω< а
Из двух интенсивных переменных Т и р лишь одна
является свободной
 Т – свободная переменная (выбор)
Т – свободная переменная (выбор)
р=р(Т ) – уравнение линии L 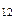 = L
= L 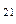 , принадлежащей обеим фазам 1 и 2.
, принадлежащей обеим фазам 1 и 2.
 Изображение результата в пространстве Т – р
Изображение результата в пространстве Т – р
В пространстве Т – р для обеих фаз 1 и 2 имеется одна общая линия L 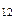 = L
= L 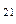 , где эти фазы способны к равновесному сосуществованию друг с другом; она лежит на пересечении двух областей D
, где эти фазы способны к равновесному сосуществованию друг с другом; она лежит на пересечении двух областей D 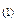 и D
и D 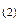 и называется двойной линией (рис. 2).
и называется двойной линией (рис. 2).
4.6.4. Трехфазная система (А=3).
ω = 3 – А = 3-3 =0.

 ω<а
ω<а
Из двух интенсивных переменных Т и р
ни одна не является свобной.
 Изображение результата в пространстве Т – р
Изображение результата в пространстве Т – р
В пространстве Т – р для всех трех фаз 1, 2 и 3 имеется одна об- щая точка Ρ 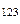 =Р
=Р 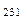 =Р
=Р 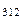 , где эти фазы способны к равновесному со-
, где эти фазы способны к равновесному со-
существованию друг с другом; она лежит на пересечении трех линий:
L 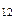 = L
= L 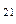 , L
, L 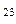 = L
= L 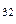 , L
, L 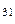 = L
= L 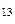 и называется тройной точкой (рис. 3).
и называется тройной точкой (рис. 3).
4.6.5. Диаграмма Т – р.
Графическое изображение в пространстве Т – р областей D 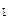 , D
, D 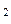 ,…, двойных линий L
,…, двойных линий L 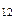 = L
= L 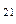 , L
, L 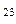 = L
= L 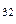 ,…, тройных точек Ρ
,…, тройных точек Ρ 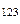 =Р
=Р 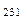 =Р
=Р 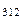 ,… для однокомпонентной системы называется диаграммой Т – р этой системы (или диаграммой фазовых равновесий в ней), диаграммой Т – р чистого вещества (или диаграммой фазовых равновесий в нём).
,… для однокомпонентной системы называется диаграммой Т – р этой системы (или диаграммой фазовых равновесий в ней), диаграммой Т – р чистого вещества (или диаграммой фазовых равновесий в нём).
Анализ двухкомпонентных систем с помощью правила фаз Гиббса.
Общие соотношения.
1) К=2, R=0, L=0;
2) а = 2 + (К-1)А = 2 + (2-1)А = 2 + А;
3) {Т, р, {N 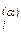 }
} 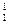 }={Т, р, {N
}={Т, р, {N 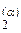 }
} 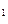 };
};
4) ω =2 + К – А – R – L = 2+2-А-0-0 = 4 – А;
5) А ≤ 2 + К – R – L = 2+2-0-0 = 4.
4.7.2. Однофазная система (А=1).
а = 2 + А = 2+1 = 3,
 {Т, р, {N
{Т, р, {N 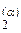 }
} 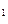 }= {Т, р, {N
}= {Т, р, {N 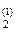 }
}
ω = 4 – А = 4-1 = 3.
 ω = а
ω = а
Из трех интенсивных переменных Т , р, N 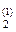 все являются
все являются
свободными
 Изображение результата в пространстве Т – р-N
Изображение результата в пространстве Т – р-N 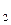
В пространстве Т – р– N 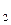 для фазы 1 имеется некоторая область D
для фазы 1 имеется некоторая область D 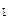 , где эта фаза способна к равновесному существованию автономно (рис.1).
, где эта фаза способна к равновесному существованию автономно (рис.1).
4.7.3. Двухфазная система (А=2).
а = 2 + А = 2+2 = 4,
 {Т, р, {N
{Т, р, {N  }
}  }= {Т, р, N
}= {Т, р, N 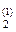 , N
, N 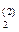 },
},
ω = 4 – А = 4-2 = 2.
 ω< а
ω< а
Из четырех интенсивных переменных Т, р, N 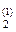 , N
, N 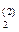
лишь две являются свободными
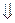 Т и р – свободные переменные (выбор)
Т и р – свободные переменные (выбор)
N 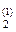 = N
= N 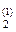 ( Т , р) – уравнение поверхности S
( Т , р) – уравнение поверхности S 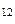 для фазы 1,
для фазы 1,
N 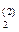 = N
= N 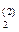 ( Т , р) – уравнение поверхности S
( Т , р) – уравнение поверхности S 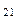 для фазы 2.
для фазы 2.
 Изображение результата в пространстве Т – р – N
Изображение результата в пространстве Т – р – N 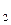
В пространстве Т – р – N 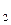 для каждой из двух фаз 1 и 2 имеется одна из двух поверхностей S
для каждой из двух фаз 1 и 2 имеется одна из двух поверхностей S 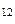 и S
и S 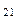 , где данная фаза способна к равновесному сосуществованию с другой; упомянутые поверхности являются границами соответствующих областей D
, где данная фаза способна к равновесному сосуществованию с другой; упомянутые поверхности являются границами соответствующих областей D 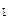 и D
и D 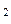 (рис.2).
(рис.2).
4.7.4. Трехфазная система (А=3).
а = 2 + А = 2+3 = 5,
{Т, р, {N 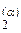 }
} 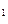 }= {Т, р, N
}= {Т, р, N 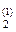 , N
, N 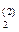 , N
, N 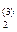 }
}
ω = 4 – А = 4-3 = 1.
 ω< а
ω< а
Из пяти интенсивных переменных Т, р, N 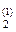 , N
, N 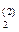 , N
, N 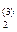 лишь одна
лишь одна
является свободной
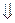 Т – свободная переменная (выбор)
Т – свободная переменная (выбор)
N 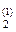 = N
= N 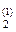 (Т ) и р=р(Т ) – уравнение линии L
(Т ) и р=р(Т ) – уравнение линии L 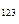 для фазы 1,
для фазы 1,
N 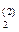 = N
= N 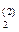 (Т ) и р=р(Т ) – уравнение линии L
(Т ) и р=р(Т ) – уравнение линии L 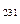 для фазы 2,
для фазы 2,
N 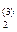 = N
= N 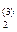 (Т ) и р=р(Т ) – уравнение линии L
(Т ) и р=р(Т ) – уравнение линии L 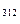 для фазы 3.
для фазы 3.
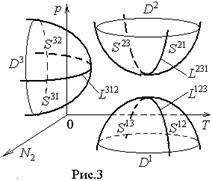
 Изображение результата в пространстве Т – р – N
Изображение результата в пространстве Т – р – N 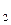
В пространстве Т – р – N 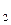 для каждой из трех фаз 1, 2, 3 имеется одна из трех линий L
для каждой из трех фаз 1, 2, 3 имеется одна из трех линий L 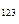 , L
, L 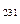 , L
, L 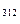 , где данная фаза способна к равновесному сосуществованию с остальными; упомянутые линии – стыки поверхностей S
, где данная фаза способна к равновесному сосуществованию с остальными; упомянутые линии – стыки поверхностей S 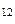 и S
и S 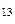 , S
, S 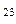 и S
и S 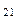 , S
, S 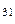 и S
и S 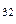 соответственно (рис.3).
соответственно (рис.3).
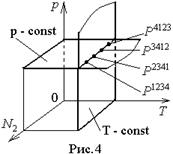
4.7.5. Четырехфазная система (А=4).
а = 2 + А = 2+4= 6,
 {Т, р, {N
{Т, р, {N 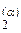 }
} 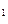 }= {Т, р, N
}= {Т, р, N 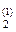 , N
, N 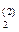 , N
, N 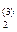 , N
, N 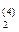 },
},
ω = 4 – А = 4-3 = 1.
 ω< а
ω< а
Из шести интенсивных переменных Т, р, N 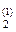 , N
, N 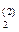 , N
, N 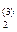 , N
, N 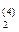
ни одна не является свободной.
 Изображение результата в пространстве Т – р – N
Изображение результата в пространстве Т – р – N 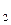
В пространстве Т – р – N 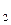 для каждой из четырех фаз 1, 2, 3, 4 имеется одна из четырех точек P
для каждой из четырех фаз 1, 2, 3, 4 имеется одна из четырех точек P 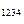 , P
, P 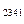 , P
, P 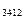 , P
, P 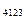 , где данная фаза способна к равновесному сосуществованию с остальными (рис.4); каждая такая точка – стык трех линий, принадлежащих одной и той же фазе и обеспечивающих её равновесные сосуществования с каждыми двумя из трех остальных фаз (эти линии на рис.4 не показаны).
, где данная фаза способна к равновесному сосуществованию с остальными (рис.4); каждая такая точка – стык трех линий, принадлежащих одной и той же фазе и обеспечивающих её равновесные сосуществования с каждыми двумя из трех остальных фаз (эти линии на рис.4 не показаны).
4.7.6. Диаграмма Т – р – N 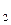 .
.
Графическое изображение в пространстве Т – р – N 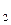 областей D
областей D 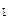 , D
, D 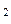 ,…, поверхностей S
,…, поверхностей S 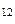 , S
, S 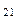 ,…, линий L
,…, линий L 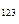 , L
, L 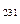 ,…, точек P
,…, точек P 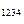 , P
, P 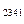 ,… для двухкомпонентной системы называется диаграммой Т – р – N
,… для двухкомпонентной системы называется диаграммой Т – р – N  этой системы (или диаграммой фазовых равновесий в ней).
этой системы (или диаграммой фазовых равновесий в ней).
