Среднеквадратическое отклонение

Среднеквадратическое отклонение – это число, равное квадратному корню из дисперсии:

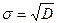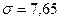, (1.3.1)

Коэффициент вариации V

На практике широко применяют также характеристику рассеяния, называемую коэффициентом вариации V, который представляет собой отношение среднего квадратичного отклонения к среднему значению. Коэффициент вариации показывает насколько велико рассеяние по сравнению со средним значением случайной величины. Коэффициент вариации выражается в долях единицы или в процентах. Вычисление коэффициента вариации имеет смысл для положительных случайных величин:

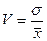(1.4.1)

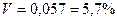
Отбраковка по критерию Шовене

При проведение опытов при одинаковых условиях часто наблюдаются значения, резко отличающиеся от остальных. Отбраковка таких значений производится с помощью специальных методов. В работе мы использовали критерий Шовене.

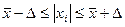, (1.5.1)

где 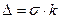, k – коэффициент Шовене, для n=52 он равен 2,68.

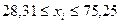, все элементы выборки вошли в интервал.

Правило «трёх сигм»

Правило «трёх сигм» основано на том, что случайная величина при нормальном законе распределения практически полностью (на 99,7%) заключена в пределах от 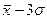до 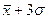. Если значение случайной величины отличается от среднего значения 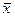больше чем на 3 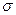, то оно является аномальным.

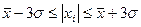(1.6.1)

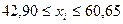, все элементы выборки вошли в интервал.

Интервальная оценка параметров выборки

Интервальная оценка с принятой вероятностью p или уровнем значимости 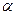определяет диапазон, в котором с определённой вероятностью будет находится истинное значение средней величины

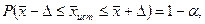(1.7.1)

где Р – это доверительная вероятность, α – уровень значимости

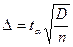, (1.7.2)

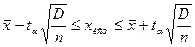(1.7.3)

k=n-1, (1.7.4)

где k – степень свободы, 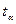- критерий Стьюдента, для 52 равен 2,1008 с α=0,05.

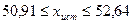
Необходимое и достаточное количество экспериментов

Зависит от точности, которую нам нужно получить.

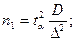(1.8.1)

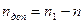(1.8.2)

где n – это количество экспериментов, которое у нас было.

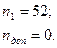
Проверка закона распределения

Нормальный закон распределения выполняется в том случае, если соблюдается два условия:

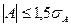(1.9.1)

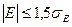(1.9.2)

где A – показатель ассиметрии (характеризует симметричность левой и правой ветвей кривой), равный

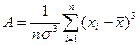. (1.9.3)

А= 0,028

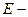показатель эксцесса (характеризует форму вершины кривой),

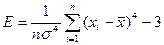, (1.9.4)

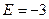
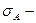среднеквадратическое отклонение ассиметрии нормального закона.

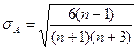, (1.9.5)

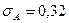
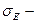среднеквадратическое отклонение эксцесса нормального распределения

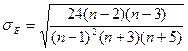, (1.9.6)

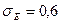
Оба условия выполнены, следовательно, выборка подчиняется нормальному закону распределения.

Группировка данных

Весь диапазон данных разбивают на классы.

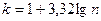(1.10.1)

где 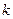- количество классов. 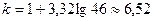. Результат округляем до целого. Размер каждого класса находим по формуле:

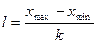(1.10.2)

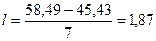
Таблица №2

Номер класса	Класс	Количество данных	Частость
Дол. единиц	%
	45,43 – 47,38		0,077	7,7
	47,38 –49,33		0,269	26,9
	49,33 –51,28		0,308	30,8
	51,28 –53,23		0,192	19,2
	53,23 –55,18		0,115	11,5
	55,18 –57,13		0,019	1,9
	57,13 – 58,49		0,019	1,9

Проверка: 1 100

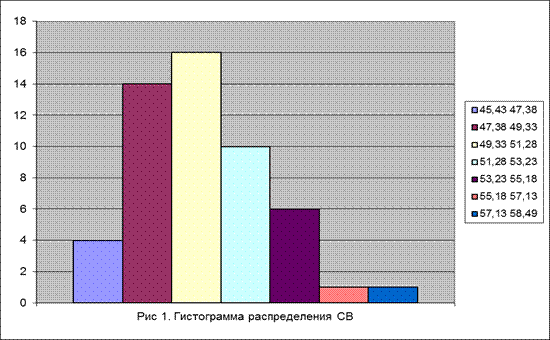
Рис. 1.10. Гистограмма.

Вывод

В данной работе были закреплены знания о статистических оценках выборки: среднеарифметической выборки, дисперсии, среднеквадратичного отклонения, коэффициента вариации. Было так же определено количество экспериментальных опытов, которые в дальнейшем я проверил по закону распределения случайной величины. Для наглядной оценки данной ситуации я построил гистограмму, что значительно упрощает задачу и делает ее на много проще.