Выберите правильное тождество для определения функции ненадежности Q(t)

			Q(t) = 1 - F(t)
	Состояние объекта, при котором он неспособен выполнить требуемую функцию по любой причине. Неработоспос.сост. · Вопр   Состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно технической и (или) конструкторской (проектной) документации. Работоспособн.       Объект, для которого в рассматриваемой ситуации проведение восстановления работоспособного состояния предусмотрено в нормативно технической и (или) конструкторской (проектной) документации, будет являться восстанавливаемый объект Объект, для которого в рассматриваемой ситуации проведение восстановления работоспособного состояния не предусмотрено в нормативно технической и (или) конструкторской (проектной) документацией Невосстанавливаемый объект

	Состояние объекта, при котором он соответствует всем требованиям нормативно-технической и (или) конструкторской (проектной) документации. исправное · Вопр   Состояние объекта, характеризующееся неспособностью выполнить требуемую функцию, исключая такую неспособность во время планового технического обслуживания или других запланированных действий или из-за нехватки внешних ресурсов. Неисправность.   Явления, процессы, события и состояния, обусловленные возникновением отказа объекта. Последствия отказа                   Средней наработкой до отказа объекта называется _____________ наработки объекта до отказа. Математич.ожидание

Вопрос 7

	Многократно возникающий самоустраняю­щийся отказ одного и того же характера Перемежающийся

· Вопрос 8

	Отказ, возникающий в результате постепенного изменения одного или нескольких параметров объекта. постепенный

· Вопрос 9

	[X] свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или наработки. безотказность

· Вопрос 11

	Отказ, в результате которого происходит снижение дифференциального выходного эффекта объекта или не обеспечивается получение заданного значения интегрального выходного эффекта. Частичн.отказ

· Вопрос 12

	_______ - продолжительность или объем работы объекта, измеряемые в часах, циклах или других единицах. наработка

· Вопрос 14

	Математическое ожидание - это средняя наработка объекта до ________.отказа

· Вопрос 15

	Функцией _________ называют вероятность отказа объекта на интервале (0, t). Ненадежности

· Вопрос 16

	_________ надежности называют вероятность того, что случайная величина наработки до отказа будет не менее заданной наработки, отсчитываемой от начала эксплуатации. Функцией

· Вопрос 18

	Плотность распределения наработки до отказа при расчете показателей надежности трубчатого разрядника … уменьшается

	_________ - продолжительность или объем работы объекта, измеряемая в часах, мото-часах, гектарах, километрах пробега, циклов включений и др. Наработка

	_________ - это условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для заданной наработки при условии, что до этой наработки отказ не возник.

Интенсивность отказов.

____________ - последовательность отказов, возникающих одним за другим в случайные моменты времени (при записи используйте пробел). Поток отказов Отказ, характеризующийся скачкообразным изменением значений одного или нескольких параметров объекта     Внезапный отказ

Состояние объекта, при котором его дальнейшая эксплуатация недопустима или нецелесообразна, либо восстановление его работоспособного состояния невозможно или нецелесообразно

Предельное состояние

Многократно возникающий самоустраняю­щийся отказ одного и того же характера

Перемежающийся отказ

Состояние объекта, при котором он неспособен выполнить хотя бы одну из нескольких требуемых функций

Частичный отказ

Отказ, не обусловленный другими отказами

Независимый

Параметрический подход основан на использовании моделей отказов нагрузка - прочность и параметр - поле допуска. Применение таких моделей возможно тогда, когда имеется информация о закономерностях распределений и процессов изменений прочности или определяющих параметров объектов, а также параметров нагрузок или допустимых значений параметров. Параметрический подход болееточен, чем непараметрический, однако расчет при параметрическом подходе сложнее.

Под ____ структурной схемой надежности ____ понимается наглядное (графическое) представление условий, при которых работает или не работает исследуемая система (при ответе используйте пробел).

Средняя наработка ____на отказ_ — для невосстанавливаемых (неремонтируемых) систем - это математическое ожидание времени работы системы до отказа.

Работоспособное состояние не функционирования объекта в нетребуемое время

Свободное состояние

Состояние объекта, при котором он выполняет требуемую функцию для потребителя (потребителей) и по этой причине недоступен для других потребителей

		Свободное состояние
		Занятое состояние
		Состояние предотказа
		Исправное состояние

Плотность распределения наработки до отказа является ___________ формой закона распределения наработки до отказа

дифференциальной

Объект, представляющий собой простейшую часть системы, отдельные части которого не представляют самостоятельного интереса в рамках конкретного рассмотрения

		Элемент
		Система
		Невосстанавливаемый объект
		Объект

Свойства функции усталости:

ϕ= = ( 0) 1 t ;

lim ϕ (t)= 0

t →∞

Истина

Ложь

Математическое ожидание - это средняя наработка объекта до ________.

Отказа

Функция ______ определяет вероятность того, что объект не только окажется работоспособен в момент времени t, но и проработает безотказно на заданном интервале (t, t + x).

		ненадежности
		оперативной готовности
		интенсивности
		ненадежности

Многократно возникающий самоустраняю­щийся отказ одного и того же характера

		Случайный отказ
		Мгновенный отказ
		Перемежающийся отказ
		Внезапный отказ

Неработоспособное состояние объекта, при котором он неспособен выполнить требуемую функцию из-за отсутствия или нехватки внешних ресурсов

		Неработоспособное состояние по внешней причине
		Неработоспособное состояние объекта
		Неработоспособное состояние системы
		Неработоспособное состояние по внутренней причине

Моментные функции параметров распределения f(x, t) аппроксимируются зависимостями:

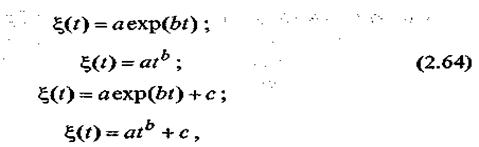
Истина

Ложь

Вероятность безотказной работы (функция надежности невосстанавливаемой системы) равна произведению вероятностей безотказной работы элементов.

Истина

Ложь

Неработоспособное состояние объекта, при котором он неспособен выполнить требуемую функцию из-за внутренней неисправности или планового технического обслуживания

		Неработоспособное состояние по внешней причине
		Состояние предотказа
		Неработоспособное состояние по внутренней причине
		Неисправное состояние системы

Отказ наспупает, когда случайная величина прочности окажется меньше случайной величины нагрузки.

Истина

Ложь

Границы поля допуска в модели отказа «параметр – поле допуска» не могут задаваться...

		неслучайной величиной
		случайной величиной
		стационарным или нестационарным случайным процессом
		временем

Назовите показатель надежности, учитывающий число отказов в единицу времени, отнесенное к среднему числу элементов, безотказно работающих в данный промежуток времени.

		интенсивность отказов
		частота отказов
		вероятность отказа
		средняя наработка до отказа

Лабораторным испытаниям подверглось 200 устройств. Через 1000 часов отказало 50 устройств, а еще через 500 часов отказало 20 устройств. Определите вероятность безотказной работы для интервала времени 1000 – 1500 часов.

		0,867
		0,65
		0,25
		0,1

Выберите показатель надежности, который не может характеризовать надежность невосстанавливаемого объекта.

		вероятность безотказной работы
		интенсивность отказов
		коэффициент готовности
		средняя наработка до отказа

модель отказа «параметр – поле допуска» позволяет установить аналитическую связь:

		между функциями усталости
		между изменением параметра и показателями надежности
		между функцией усталости и изменением параметра
		между функцией усталости и показателями надежности

Выберите правильное значение области изменения функции ненадежности Q(t) для невосстанавливаемого объекта.

		- ∞ ≤ Q(t) ≤ +∞
		- ∞ ≤ Q(t) ≤ 0
		0 ≤ Q(t) ≤ 1
		0 ≤ Q(t) ≤ +∞

При уменьшении математического ожидания прочности вероятность отказа возрастает.

Истина

Ложь

Выберите правильное тождество для определения функции надежности (i = 1…n-1 – состояния предотказа, P_i (t) – вероятность i – того состояния).

		F(t) = Σ n-1i=1 Pi (t)
		F(t) = Σ ni=1 Pi (t)
		F(t) = Σ n-2i=1 Pi (t)
		F(t) = Σ n+1i=1 Pi (t)

Выберите правильное определение для интенсивности отказов.

		интенсивность отказов – вероятность того, что в пределах заданной наработки отказ объекта не возникает
		интенсивность отказов – математическое ожидание наработки объекта до первого отказа
		интенсивность отказов – условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник
		это частичная или полная утрата свойств элемента, которая существенным образом снижает или приводит к полной потере работоспособности. Отказ наступает всякий раз, когда устройство не сохраняет своих параметров в заданных пределах

На испытание было поставлено 1000 однотипных устройств. За 3000 часов отказало 20 устройств. Определить функцию надежности (вероятность безотказной работы) F(3000).

		0,95
		0,98
		0,05
		0,02

На подстанции находится пять силовых трансформаторов. Известно время безотказной работы каждого из них (t₁ = 11 лет, t₂ = 13 лет, t₃ = 16 лет, t₄ = 14 лет, t₅ = 12 лет). Выберите правильное значение среднего времени безотказной работы трансформатора по статистическим данным.

		13,2
		52,8

В модели отказа «нагрузка и прочность – случайные процессы» прочность – это

		стационарный процесс с монотонно убывающим математическим ожиданием
		стационарный процесс с монотонно возрастающим математическим ожиданием
		нестационарный случайный процесс с монотонно убывающим математическим ожиданием
		нестационарный случайный процесс с монотонно возрастающим математическим ожиданием

Выберите правильное выражение для определения коэффициент вариации прочности объекта (μ_нагр – математическое ожидание нагрузки, μ_проч – математическое ожидание прочности, σ_нагр – среднеквадратичное отклонение нагрузки, σ_проч – среднеквадратичное отклонение прочности).

		υпроч = μпроч / σпроч
		υпроч = σпроч / μпроч
		υпроч = μпроч / σнагр
		υпроч = σнагр / σпроч

Выберите правильное тождество для определения одного из свойств функции надежности F(t).

		lim F(t) = 0 при t→∞
		lim F(t) = 1 при t→∞
		lim F(t) = 0,5 при t→∞
		lim F(t) = ∞ при t→∞

Выберите правильное тождество для определения одного из свойств функции усталости.

		φ(t = 0) = 0
		φ(t = 0) = 1
		φ(t = 0)= + ∞
		φ(t = 0)= – ∞

Выберите правильное выражение для определения вероятности безотказной работы невосстанавливаемого объекта на интервале времени (t₁, t₂).

		P(t1,t2) = P(t1) + P(t2)
		P(t1,t2) = P(t1) - P(t2)
		P(t1,t2) = P(t1)/P(t2)
		P(t1,t2) = P(t2)/P(t1)

Надежность работы устройства описывается экспоненциальным законом распределения. Выберите правильное выражение для определения функции надежности (вероятности безотказной работы) изделия.

		F(t) = e-λt
		F(t) =1 – e-λt
		F(t) = λ∙e-λt
		F(t) = 1 / λ

Если коэффициент вариации прочности возрастает, то вероятность отказа …

		Возрастает
		Уменьшается
		Неизменна
		возрастает, а потом уменьшается

На испытание было поставлено 10 однотипных электрических ламп. За 1000 часов отказало 2 лампы. За следующий интервал времени Δt = 100 часов отказало еще n(Δt) = 1 лампа. Определить величину интенсивности отказов λ (t, t + Δt) на интервале Δt = 100 часов.

		0,03 1/ч
		333,3 х 10-5 1/ч
		425 х 10-5 1/ч
		0,33 1/ч

В модели отказа "параметр - поле допуска" границы поля допуска задаются ...

		только неслучайной величиной
		только стационарным случайным процессом
		только случайной или неслучайной величиной
		случайной или неслучайной величиной, а также стационарными или нестационарными процессами

За время эксплуатации 100 объектов отказало 20 объектов. Выберите правильное значение вероятности отказа.

		0,8
		0,2
		0,25
		0,5

Какое количество участков имеется на классической кривой изменения интенсивности отказов в функции наработки?

		два
		три
		пять
		один

Основным показателем безотказности невосстанавливаемых объектов является функция надежности F(t) – вероятность того, что в пределах заданной наработки t отказ объекта не возникает. Функция F(t) имеет ряд свойств. Среди приведенных ниже, укажите одно неверное свойство.

		F(0) = 1
		F (t) = 0 (при t → ∞)
		0 ≤ F(t) ≤ 1
		-∞ ≤ F(t) ≤ +∞

Надежность работы устройства описывается законом распределения Релея. Выберите правильное выражение для определения функции надежности (вероятности безотказной работы) изделия (a, k - параметры закона распределения Вейбулла).

		F(t) = exp( –( t2 / 2σ2))
		F(t) =1– exp( – (t2 / 2σ2))
		F(t) =(t / σ2) × exp( – (t2 / 2σ2))
		F(t) = σ × √(π / 2)

Какой из перечисленных объектов наиболее близко относится к классу невосстанавливаемых объектов?

		инверторный агрегат
		тиристор
		выключатель переменного тока
		силовой трансформатор

Функция надежности (вероятности безотказной работы) F(t) и вероятность появления отказа Q(t) являются …

		функция F(t) монотонно убывающей, функция Q(t) – монотонно убывающей
		функция F(t) монотонно убывающей, функция Q(t) – монотонно возрастающей
		функция F(t) монотонно возрастающей, функция Q(t) – монотонно убывающей
		функция F(t) монотонно возрастающей, функция Q(t) – монотонно возрастающей

Функция надежности – это показатель

		долговечности объекта
		ремонтопригодности объекта
		безотказности объекта
		сохраняемости объекта

В работе находилось 4 изделия. Известно время безотказной работы каждого изделия t₁ = 12 ч, t₂ = 14 ч, t₃ = 20 ч, t₄ = 10 ч. Выберите правильное значение среднего времени безотказной работы изделия.

		10 ч
		20 ч
		14 ч
		12 ч

Выберите правильное выражение для определения интенсивности отказов невосстанавливаемых объектов λ(t) (n(Δt) – число отказавших изделий в единицу времени, N_СР – среднее число исправно работающих изделий).

		λ(t) = n(Δt) / (NСР× Δt)
		λ(t) = (n(Δt) × Δt) / NСР
		λ(t) = Δt / (n(Δt)× NСР)
		λ(t) = n(Δt) / NСР

Выберите правильное выражение для определения дисперсии суммы независимых случайных величин.

		D(X1 + X2 + X3) = D (X1) × D (X2) × D (X3)
		D (X1 + X2 + X3) = D (X1) + D (X2) + D (X3)
		D (X1 + X2 + X3) = D (X1) / (D (X2) × D (X3))
		D (X1 + X2 + X3) = D (X1) – D (X2) – D (X3)

Известны вероятности безотказной работы изделия для моментов времени t₁ и t₂. P(t₁) = 0,8; . P(t₂) = 0,6. Выберите правильное значение вероятности безотказной работы на интервале времени (t₁, t₂).

		P (t1, t2) = 0,48
		P (t1, t2) = 0,2
		P (t1, t2) = 0,75
		P (t1, t2) = 0,12

Имеется выборка из дискретных значений индекса цветопередачи (Ra) для четырех различных типов ламп.

Х₁ = 85; Х₂ = 90; Х₃ = 75; Х₄ = 80

Выберите правильное значение математического ожидания данной выборки.

		82,5

Параметры надежности невосстанавливаемых объектов: F(t) – функция надежности (вероятность безотказной работы), f(t) – частота отказов, λ(t) – интенсивность отказов - связаны между собой некоторым соотношением. Укажите правильное.

		f(t) = λ(t)∙F(t)
		f(t) = λ(t)/F(t)
		f(t) = F(t)/ λ(t)
		f(t) = λ(t) + F(t)

Какой из перечисленных объектов наиболее близко относится к классу невосстанавливаемых ремонтопригодных объектов?

		диодный вентиль
		артиллерийский снаряд
		баллистическая ракета
		печатная плата

Чему равно среднее время работы до отказа (наработка на отказ) при экспоненциальном законе надежности?

		μ(t) = 1/λ2
		μ(t) = 1/λ
		μ(t) = λ
		μ(t) = λ2

Выберите правильное тождество для нахождения среднеквадратичное отклонение выборки дискретных случайных величин.

		σ = √D
		σ = 3√D
		σ = μ2
		σ = μ + D

Выберите правильное выражение для определения математического ожидания суммы случайных величин.

		μ(X1 + X2 + X3) = μ(X1) × μ(X2) × μ(X3)
		μ(X1 + X2 + X3) = μ(X1) +μ(X2) + μ(X3)
		μ(X1 + X2 + X3) = μ(X1) / (μ(X2) × μ(X3))
		μ(X1 + X2 + X3) = μ(X1) – μ(X2) – μ(X3)

Выберите правильное выражение для определения коэффициент запаса (μ_нагр – математическое ожидание нагрузки, μ_проч – математическое ожидание прочности, σ_нагр – среднеквадратичное отклонение нагрузки, σ_проч – среднеквадратичное отклонение прочности).