Орієнтовний перелік питань для підсумкового контролю знань
МЕТОДИЧНІ ВКАЗІВКИ
ТА ІНДИВІДУАЛЬНІ ЗАВДАННЯ
з курсу «ВИЩа МАТЕМАТИКа»
ЗА ТЕМОЮ «Диференціальне числення функцій
однієї змінної» для студентів І курсу
денної форми навчання
Затверджено на засіданні
кафедри комп’ютерних
технологій та вищої математики.
Протокол № 11 від 26.06.2009.
Дніпропетровськ УДХТУ 2010
Методичні вказівки та індивідуальні завдання з курсу «Вища математика» за темою «Диференціальне числення функцій однієї змінної» для студентів І курсу денної форми навчання / Укл.: О.А. Радуль, Т.Ю. Ускова, Д.Г. Зеленцов. – Дніпропетровськ: ДВНЗ УДХТУ, 2010. – 28 с.
Укладачі: О.А. Радуль
Т.Ю. Ускова
Д.Г. Зеленцов
Відповідальний за випуск Д.Г. Зеленцов, д-р техн. наук
Навчальне видання
Методичні вказівки та індивідуальні завдання
з курсу «Вища математика» за темою «Диференціальне числення
функцій однієї змінної» для студентів І курсу денної форми навчання
Укладачі: РАДУЛЬ Оксана Анатоліївна
УСКОВА Тетяна Юріївна
ЗЕЛЕНЦОВ Дмитро Гєгємонович
Редактор Л.М. Тонкошкур
Коректор Л.Я. Гоцуцова
Підписано до друку 30.03.10. Формат 60´84 1/16. Папір ксерокс. Друк різограф. Ум.-друк. акр. 1,28. Обл.-вид. арк. 1,34. Тираж 100 прим. Зам. № 122. Свідоцтво ДК № 303 від 27.12.2000.
ДВНЗ УДХТУ, 49005, м. Дніпропетровськ-5, просп. Гагаріна, 8.
Видавничо-поліграфічний комплекс ІнКомЦентру
ЗМІСТ
ВСТУП.. 4
ОСНОВНІ ПИТАННЯ ПРОГРАМИ ДИСЦИПЛІНИ ЗА ТЕМОЮ «ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ». 4
ОРІЄНТОВНИЙ ПЕРЕЛІК ПИТАНЬ ДЛЯ ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ 5
1. ВИЗНАЧЕННЯ ПОХІДНОЇ. ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ.. 5
Завдання 1. 9
2. ГЕОМЕТРИЧНЕ ЗАСТОСУВАННЯ ПОХІДНОЇ 17
Завдання 2. 18
3. ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ, ЗАДАНИХ ПАРАМЕТРИЧНО.. 19
Завдання 3. 20
4. ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ, ЗАДАНИХ НЕЯВНО.. 21
Завдання 4. 22
Завдання 5. 24
5. ПРАВИЛО ЛОПІТАЛЯ.. 24
Завдання 6. 26
СПИСОК ЛІТЕРАТУРИ.. 28
ВСТУП
Методичні вказівки відповідають програмі курсу «Вища математика» та можуть використовуватичя при виконанні індивідуальних завдань за темою «Диференціальне числення функцій однієї змінної».
Особливістю видання є наявність завдань для тетраместрових індивідуальних робіт у кількості, достатньої для академічних груп.
Метою запропонованих методичних вказівок є допомога тим, хто вивчає диференціальне числення, придбати навички розв’язання стандартних задач.
Рекомендується перед виконанням індивідуальних завдань, ознайомитися з теорією й розв’язками типових прикладів викладених у даних методичних вказівках.
Слід мати на увазі, що це – не навчальна книга, не конспект лекцій, а короткий довідковий матеріал, який не може замінити вивчення лекційного матеріалу та навчальної літератури.
ОСНОВНІ ПИТАННЯ ПРОГРАМИ ДИСЦИПЛІНИ ЗА ТЕМОЮ «ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ
ОДНІЄЇ ЗМІННОЇ»
| 1. Похідна функції. Її геометричний та фізичний зміст: | |
| Поняття похідної та її означення. Геометричний та механічний зміст похідної. Теореми про зв’язок диференційованості та неперервності функції. | |
| 2. Диференційованість функції: | |
| Поняття диференційованості функції в точці. Зв’язок між поняттями диференційованості та неперервності. | |
| 3. Основні правила диференціювання: | |
| Основні правила диференціювання. Таблиця похідних найпростіших елементарних функцій. | |
| 4. Похідні інших функцій: | |
| Похідні складної функції, оберненої функції, функції, яка задана неявно, степенево-показникової функції, параметрично заданої функції. | |
| 5. Диференціал функції: | |
| Означення диференціала функції. Його геометричний зміст та застосування. Інваріантність форми першого диференціала. Формули та правила обчислення диференціалів. Наближені обчислення за допомогою диференціала. | |
| 6. Похідні та диференціали вищих порядків | |
| 7. Застосування похідної: | |
| Правило Лопіталя, інтервали монотонності функції, екстремум функції, асимптоти, умови опуклості та вгнутості функції. |
ОРІЄНТОВНИЙ ПЕРЕЛІК ПИТАНЬ ДЛЯ ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ
1. Похідна функції. Основні формули й правила диференціювання.
2. Механічна й геометрична інтерпретації похідної.
3. Теорема про зв’язок неперервності і диференційованості функції.
4. Похідна складної функції. Логарифмічна похідна.
5. Похідна оберненої функції. Похідна функції, що задана параметрично.
6. Диференціал функції. Геометричний зміст диференціала. Властивості диференціала.
7. Застосування диференціала до наближених обчислень.
8. Похідні та диференціали вищих порядків.
9. Правило Лопіталя щодо розкриття невизначеностей виду 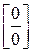 .
.
10. Правило Лопіталя щодо розкриття невизначеностей виду 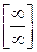 .
.
11. Ознаки монотонності функції.
12. Екстремум функції. Необхідна й достатні умови існування екстремуму.
13. Умови опуклості та увігнутості кривої.
14. Точки перегину. Необхідна й достатня умови існування точок перегину.
15. Асимптоти графіка функції. Види асимптот.
