Справочный материал по темам

«Элементы линейной алгебры. Аналитическая

геометрия в пространстве»

Матрицы

Матрицей размерности m ´ n называется прямоугольная таблица, состоящая из m·n элементов (m строк и n столбцов):

A_m´n = 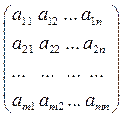, где a_ij – элементы матрицы,

i = 1,2,…, m – номер строки, j = 1,2,…, n – номер столбца.

Для краткости матрицу обозначают одной буквой, например, буквой А.

Некоторые виды матриц:

1) нулевая матрица: матрица, все элементы которой равны нулю;

2) при n = 1 матрица-столбец: X = ;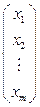

3) при m = 1 матрица-строка: Y = ;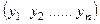

4) при m = n квадратная матрица: A_n´n = .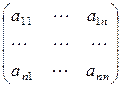

У квадратной матрицы различают главную диагональ (соединяющую элементы a₁₁ и a_nn ) и побочную диагональ.

Примеры квадратных матриц:

1) единичная матрица (квадратная матрица, на главной диагонали которой

стоят единицы, а остальные элементы – нули):

E = ;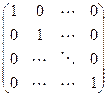

2) квадратная матрица второго порядка: ;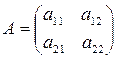

3) квадратная матрица третьего порядка: .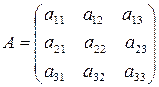

Две матрицы А и В называются равными, если они имеют одинаковые размерности и их соответствующие элементы равны:

A_m´n = B_m´n Û a_ij = b_ij (i = 1,2,…, m; j = 1,2,…, n).

Линейные операции над матрицами

Умножение матрицы A на число k:

B = k×A= ,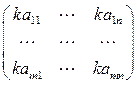

или, в краткой записи:

B = k×A Û b_ij = k×a_ij (i = 1,2,…, m; j = 1,2,…, n). (21)

Сложение (вычитание) матриц A и B одинаковой размерности:

C_m´n = A_m´n ± B_m´n Û c_ij­ = a_ij ± b_ij (i = 1,2,…, m; j = 1,2,…, n). (22)

Произведение матриц A_m´n и B_n´k:

C_m´k = A_m´n × B_n´k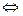

c_ij = a_i1b_1j + a_i2b_2j + ¼ + a_inb_nj (i = 1,2,…, m; j = 1,2,…, k). (23)

Формулу (23) легко запомнить, как правило умножения «строка на столбец»: произведение матриц A_m´n и B_n´k есть матрица C_m´k, у которой элемент c_ij равен сумме произведений соответствующих элементов i-й строки матрицы A и j-го столбца матрицы В.

Замечание. Перемножать можно только соответственные матрицы А и В, т.е.число столбцов матрицы А должно быть равно числу строк матрицы В.

Если задан многочлен 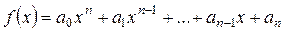, то матричным многочленом 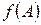называется выражение

,

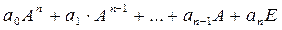где А – квадратная матрица, 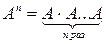и Е – единичная матрица той же размерности, что и А. Значением матричного многочлена является матрица.

Определители

Определитель второго порядка (определитель квадратной матрицы второго порядка):

det A = 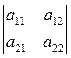= a₁₁ a₂₂ – a₁₂ a₂₁­. (24)

Определитель третьего порядка (определитель квадратной матрицы третьего порядка):

det A = 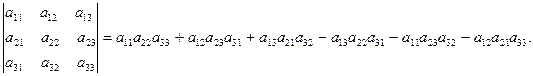(25)

Для краткости определитель обозначают: |A| или Δ.

Минором элемента a_ij определителя называется определитель, которыйполучается из исходного путем вычеркивания i-й строки и j-го столбца (обозначается M_ij).

Алгебраическим дополнением элемента a_ij определителя (обозначается A_ij) называется число:

A_ij = (–1)^i+j× M_ij. (26)

Определитель третьего порядка можно вычислить, используя его разложение по 1-й строке:

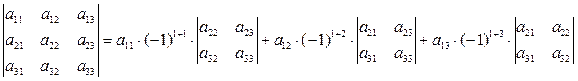, (27)

или, в краткой записи:

,

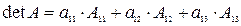т.е. определитель равен сумме произведений элементов первой строки на их алгебраические дополнения. Аналогично можно записать разложение определителя по любой другой строке или столбцу.