Задания для самостоятельного решения. Для f(x,y,z) равной единице на указанных наборах удалить несущественные переменные.
Задание №1
Для f(x,y,z) равной единице на указанных наборах удалить несущественные переменные.
Задание №2
Проверьте двумя способами а) составлением таблиц истинности; б) с помощью эквивалентных преобразований, будут ли эквивалентны формулы.
Варианты заданий:
Вариант №1
1. f(x,y,z)=(0,5,8,9,10,12,13,15)
2. 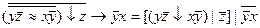
Вариант №2
1. f(x,y,z)=(0,8,,9,10,12,13,15)
2. 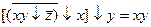
Вариант №3
1. f(x,y,z)=(1,2,3,12,13,14,15)
2. 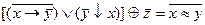
Вариант №4
1. f(x,y,z)=(2,3,7,8,10,11,12,15)
2. 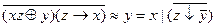
Вариант №5
1. f(x,y,z)=(0,4,6,7,8,10,13,15)
2. 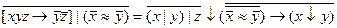
Вариант №6
1. f(x,y,z)=(0,4,5,7,8,10,11,13,15)
2. 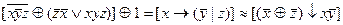
Вариант №7
1. f(x,y,z)=(0,4,5,6,7,14,15)
2. 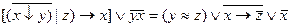
Вариант №8
1. f(x,y,z)=(2,4,7,9,10,14,15)
2. 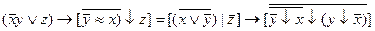
Вариант №9
1. f(x,y,z)(0,3,7,8,9,10,11,12,15)
2. 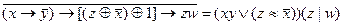
Вариант №10
1. f(x,y,z)=(0,2,4,7,8,10,13,15)
2. 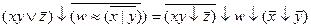
Вариант №11
1. f(x,y,z)=(0,2,4,7,8,10,13,15)
2. 
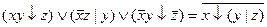
Вариант №12
1. f(x,y,z)=0,3,6,8,9,12,13,15)
2. 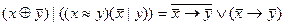
Вариант №13
1. f(x,y,z)=(2,4,7,9,10,11,13,15)
2. 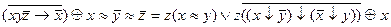
Вариант №14
1. f(x,y,z)=(2,3,4,5,9,10,11,15)
2. 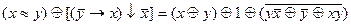
Вариант №15
1. f(x,y,z)=(5,7,8,9,10,11,15)
2. 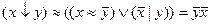
Вариант №16
1. f(x,y,z)=(2,3,4,9,10,11,14,15)
2. 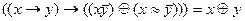
Вариант №17
1. f(x,y,z)=(0,2,4,8,12,14,15)
2. 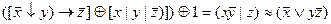
Вариант №18
1. f(x,y,z)=(2,3,4,6,8,9,11,12)
2. 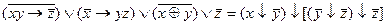
Вариант №19
1. f(x,y,z)=(5,6,7,8,9,10,11,12,13)
2. 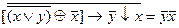
Вариант №20
1. f(x,y,z)=(3,5,7,10,11,12,13,14)
2. 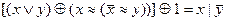
Практическая работа №5.
Тема: Специальные разложения ПФ.
Задание №1.
Для функции, заданной своими истинностными значениями, запишите: СДНФ, СКНФ и СПНФ.
f(x, y, z) = ( 1, 0, 1, 0, 0, 1, 1, 0 )
Решение: СКНФ строится по нулевым наборам, СДНФ – по единичным наборам, а СПНФ может быть получена из СДНФ путем замены «Ú» на «Å» и « 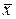 » на «xÅ1». См. таблицу .
» на «xÅ1». См. таблицу .
Таблица
| x | y | z | f(x,y,z) |
СКНФ(f(x,y,z))= 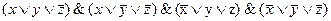 .
.
СДНФ(f(x,y,z))= 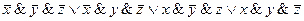 .
.
Используем тождество: aÅa=0.
СПНФ(f(x,y,z))=(xÅ1)(yÅ1)(zÅ1) Å (xÅ1)y(zÅ1) Å x(yÅ1)z Å xy(zÅ1)=(xyzÅxyÅxzÅxÅyzÅyÅzÅ1) Å (xyzÅxyÅyzÅy) Å(xyzÅxz) Å (xyzÅxy) = xzÅzÅxÅ1.
Задание №2
С помощью эквивалентных преобразований приведите формулу к виду ДНФ, КНФ, СДНФ, СКНФ.
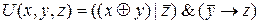
Решение: используем тождества: 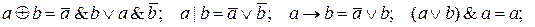
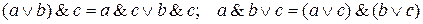
Для компактности записи вместо «a&b» , будем писать «ab».
ДНФ= 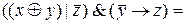
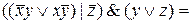
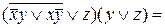
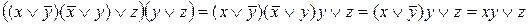
КНФ= 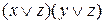
Совершенную дизъюнктивную нормальную форму (СДНФ) получим из ДНФ. Для этого к первой элементарной конъюнкции добавим единичный множитель 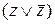 , а ко второй –
, а ко второй – 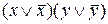 .
.
СДНФ= 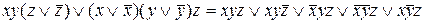
Совершенную конъюнктивную нормальную форму (СКНФ) получим из КНФ. Для этого к первой элементарной дизъюнкции добавим нулевое слагаемое 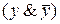 , а ко второй –
, а ко второй – 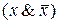 .
.
СКНФ= 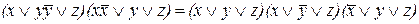
СПНФ=xyz Å xy(zÅ1) Å (xÅ1)yz Å (xÅ1)(yÅ1)z Å x(yÅ1)z = xyz Å xyz Å xy Å xyz Å yz Å xyz Å xz Å yz Å z Å xyz Å xz = xyzÅxyÅz
Задания для самостоятельного выполнения:
Задание №1
Для функции, заданной своими истинностными значениями, запишите: СДНФ, СКНФ и СПНФ.
Задание №2
С помощью эквивалентных преобразований приведите формулу к виду ДНФ, КНФ, СДНФ, СКНФ.
Варианты заданий:
Вариант №1
1. f(x,y,z)=(0,1,2,6,7,8,12,13,14)
2. 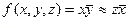
Вариант №2
1. f(x,y,z)=(4,6,8,9,11,12)
2. 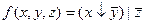
Вариант №3
1. f(x,y,z)=(0,1,2,3,6,12)
2. 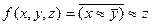
Вариант №4
1. f(x,y,z)=(0,6,10,14)
2. 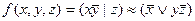
Вариант №5
- f(x,y,z)=(3,4,7)
-
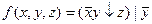
Вариант №6
- f(x,y,z)=(0, 1, 2, 3, 4)
-
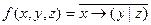
Вариант №7
- f(x,y,z)=(1, 2, 5, ,7)
-
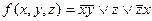
Вариант №8
- f(x,y,z)=(1, 2, 4)
-
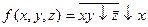
Вариант №9
- f(x,y,z)=(0, 1, 2, 3, 4, 5, 6)
-
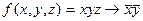
Вариант №10
- f(x,y,z)=(1, 2, 3, 4, 5, 6)
-
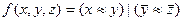
Вариант №11
- f(x,y,z)=(2, 3, 4, 5)
-
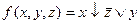
Вариант №12
- f(x,y,z)=(0, 2, 3, 4, 7)
-
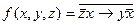
Вариант №13
- f(x,y,z)=(0, 3, 4, 6, 7)
-
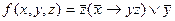
Вариант №14
- f(x,y,z)=(1, 2, 3, 7)
-
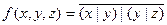
Вариант №15
- f(x,y,z)=(0, 1, 2, 5)
-
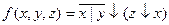
Вариант №16
- f(x,y,z)=(1, 2, 4, 5)
-
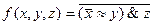
Вариант №17
- f(x,y,z)=(0, 3, 4, 7)
-
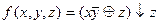
Вариант №18
- f(x,y,z)=(1, 2, 4, 5, 6)
-
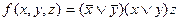
Вариант №19
- f(x,y,z)=(1,2, 3, 6)
-
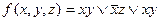
Вариант №20
- f(x,y,z)=(0, 1, 3, 4, 6, 7)
-
Практическая работа №6.
