Формула повної ймовірності

Нехай події 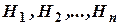утворюють повну групу подій, тобто вичерпують усі можливі результати даного експерименту. Подія 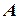може відбутися за умовою появи однієї з гіпотез 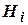з деякою ймовірністю 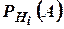. Тоді ймовірність події 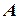обчислюється за формулою повної ймовірності

,

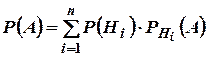де 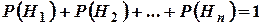, тобто дорівнює сумі добутків ймовірностей кожної з гіпотез 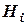на відповідну умовну ймовірність події .

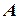Нехай тепер відомо, що результатом експерименту є подія 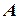. Її поява зумовить переоцінку апріорних (a priori (лат.) – відомих до спроби) ймовірностей гіпотез, які можна обчислити у цьому випадку за формулами Байєса

,

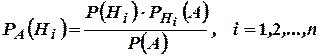де 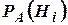– апостеріорні (a posteriori (лат.) – після експерименту) ймовірності гіпотез після випробування, коли стало відомо, що його результатом є подія 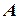; 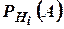– ймовірність події 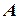при умові 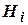; 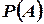– ймовірність події 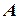, знайдена за формулою повної ймовірності.

Формули Байєса дають можливість переоцінити ймовірності гіпотез з урахуванням результату досліду.

Задача . У комп’ютерному магазині за рік продано 1000 моніторів, 300 принтерів і 100 сканерів. Протягом гарантійного терміну в сервісний центр надходять на ремонт у середньому 0,5% моніторів, 1% принтерів і 1,5% сканерів. 1) Визначити ймовірність того, що навмання вибрана з перерахованих за серійним номером одиниця товару надійде протягом гарантійного терміну на ремонт у сервісний центр. 2) Навмання вибрана з перерахованих за серійним номером одиниця товару надійшла протягом гарантійного терміну на ремонт у сервісний центр. Яка ймовірність того, що це монітор?

Розв’язання. 1) Нехай А – подія, яка полягає в тому, що навмання вибрана з перерахованих за серійним номером одиниця товару надійде протягом гарантійного терміну на ремонт у сервісний центр. Введемо гіпотези: Н₁ – подія, яка полягає в тому, що навмання вибрана з перерахованих за серійним номером одиниця товару – монітор; Н₂ – подія, яка полягає в тому, що навмання вибрана одиниця товару – принтер; Н₃ – подія, яка полягає в тому, що навмання вибрана одиниця товару – сканер. Події Н₁, Н₂, Н₃ утворюють повну групу попарно несумісних подій. За умовою задачі

, , .

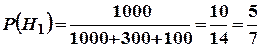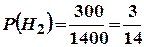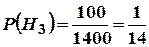Перевірка: .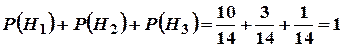

Крім того, маємо умовні ймовірності , , .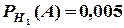

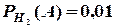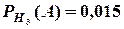За формулою повної ймовірності

.

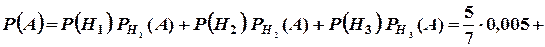
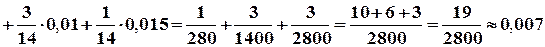2) Нехай тепер А – подія, яка полягає в тому, що навмання вибрана з перерахованих за серійним номером одиниця товару надійшла протягом гарантійного терміну на ремонт у сервісний центр. Введемо ті ж самі гіпотези Н₁, Н₂, Н₃, що й у першому пункті задачі. Тоді за формулою Байєса

.

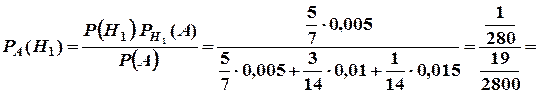
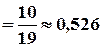Тема 5. СХЕМА БЕРНУЛЛІ.

Нехай ймовірність появи події 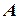в кожному з 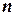незалежних аналогічних дослідів 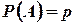є однаковою і незалежною від результатів інших спроб тієї ж серії (ймовірність протилежної події 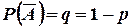). Ймовірність того, що в 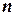дослідах рівно 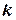разів буде успіх, тобто поява події А, обчислюється за формулою Бернуллі

.

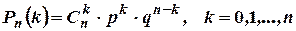Ймовірність того, що подія 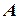відбудеться не менш ніж 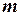разів, дорівнює

.

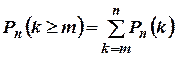Ймовірність того, що подія 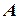настане хоча б один раз, обчислюється за формулою

.

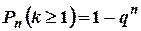Задача. Два шахісти умовились зіграти десять результативних партій. Ймовірність виграшу кожної окремої партії першим гравцем дорівнює 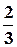, другим – 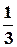(нічиї не враховуються). Чому дорівнює ймовірність: 1) виграшу всієї гри (потрібно виграти понад п’ять партій) а) першим гравцем, б) другим гравцем; 2) загального нічийного результату?

Розв’язання. Визначимо події 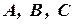: А – виграє перший гравець, В – виграє другий гравець, С – нічийний результат. Для того щоб гру виграв перший гравець, йому необхідно виграти 6, 7, 8, 9 або 10 партій. Тому, за формулою Бернуллі і теоремою додавання ймовірностей

.

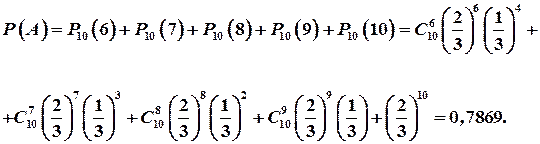
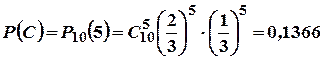Події А, В, С складають повну групу, тому

.

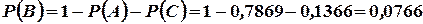ПИТАННЯ ТА ЗАВДАННЯ ДЛЯ

САМОСТІЙНОГО

ОПРАЦЮВАННЯ МАТЕРІАЛУ