Разложение периодической функции в ряд Фурье

Вопрос 1

Тригонометрическим рядом Фурье функции f(x), имеющей период T = 2l, называется ряд вида

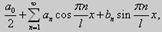в котором коэффициенты a_o, a_n, b_n вычисляются по формулам

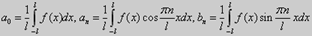,	n = 1, 2, 3, ...

При этом говорят, что ряд (53) порождён функцией f(x), а коэффициенты a_o, a_n, b_n называются коэффициентами Фурье. В случае, когда функция f(x) имеет период Т = 2π, её ряд Фурье имеет вид

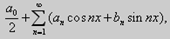
и коэффициенты Фурье вычисляются по формулам

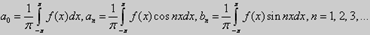
Для четных функций ряд Фурье (53) содержит только члены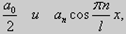

для нечетных функции - только члены 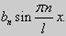В этих случаях коэффициенты Фурье удобнее вычислять по формулам

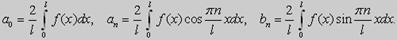
Важное значение имеют вопросы о том, при каких х ряд Фурье сходится и в каком случае сумма ряда в точке х равна значению функции f(x), порождающей этот ряд. Ответ на эти вопросы дает теорема Дирихле.

Функция f(x) на отрезке [а, b] удовлетворяет условиям Дирихле, если
a) f(x) на отрезке [а, b] непрерывна или имеет на этом отрезке конечное число точек разрыва I рода;
b) в каждом интервале непрерывности f(x) монотонна, либо имеет на этом интервале конечное число точек экстремума.

Например, функция, изображенная на рис. 22, удовлетворяет условиям Дирихле.

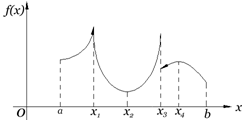
Рис.22

Теорема Дирихле. Функция f(x), периодическая с периодом Т = 2l, удовлетворяющая условиям Дирихле на отрезке [-l,l], разлагается в тригонометрический ряд Фурье (53), причем:
a) в каждой точке непрерывности х функции f(x) ряд Фурье (53) сходится к значению f(x);
b) в каждой точке разрыва х_i, функции f(x) ряд Фурье (53) сходится к значению

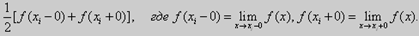
Тригонометрический ряд Фурье является частным случаем рядов, которые получаются для произвольных систем функций, ортогональных на отрезке [а, b]. Причем сами функции не обязаны быть периодическими.

Рассмотрим систему функций {φ_n(x), n = 0, 1,2,...}, ортогональную на отрезке [а, b].Рядом Фурье функции f(x)

Разложение периодической функции в ряд Фурье

Согласно гипотезе Фурье не существует функции, которую нельзя было бы разложить в тригонометрический ряд. Рассмотрим, каким образом можно провести данное разложение. Следующую систему ортонормированных функций на отрезка [–π, π] можно представить:

{1, cos(t), sin(t), cos(2t), sin(2t), cos(3t), sin(3t), …, cos(nt), sin(nt),… }

Руководствуясь тем, что данная система функций является ортонормированной, произвольную функцию f(t) на отрезке [π, –π] можно представить следующим образом:

f(t) = α0 + α1·cos(t) + α2·cos(2t) + α3·cos(3t) + …+ β1·sin(t) +...

... + β2·sin(2t) + β3·sin(3t)+… (1)

Коэффициенты αn, βn вычисляются через скалярное произведение функции и базисной функции по формулам, рассмотренным ранее, и выражаются следующим образом:

α0 = <f(t)>, 1> =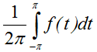

αn = <f(t)>, cos(nt) > =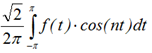

βn = <f(t)>, sin(nt) > =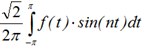

Выражение (1) можно записать в сжатом виде следующим образом:

f(t) = a0/2 + a1·cos(t) + a2·cos(2t) + a3·cos(3t) + … + b1·sin(t) + b2·sin(2t) + b3·sin(3t)+… (2)

где

a0 = 2α0 =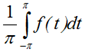

an = αn =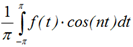

bn = βn =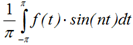

Так как при n = 0 cos(0) = 1, константа a0/2 выражает общий вид коэффициента an при n = 0.

an =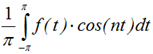

bn = 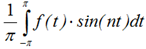(3)

Вопрос 4