Экспериментальна проверка закона Малюса

Кафедра физики

Лабораторная работа № 8

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА

ЗАКОНОВ ПОЛЯРИЗАЦИИ СВЕТА

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА

ЗАКОНОВ ПОЛЯРИЗАЦИИ СВЕТА

Цель работы: заключается в знакомстве с двумя основными законами поляризации света - законами МАЛЮСА и БРЮСТЕРА, и в их экспериментальной проверке с помощью лабораторных установок.

В данной работе предполагается проделать следующее:

1. Познакомиться с основными теоретическими сведениями о поляризованном свете и соответствующими законами.

2. Осуществить экспериментальную проверку закона Малюса.

3. Осуществить экспериментальную проверку закона Брюстера.

Теоретические сведения

Свет представляет собой сложное явление: в одних случаях он ведет себя как волна (электромагнитная), в других - как поток особых частиц - фотонов. В связи с этим теория света называется корпускулярно - волновой. В данной работе будут изучаться некоторые явления (и законы), в основе которых лежит волновая природа света.

Как известно из теории Максвелла, в электромагнитной волне происходят колебания двух физических величии - напряженностей электрического и магнитного полей, характеризуемых векторами Е и Н ( рис. 1) В основном, при взаимодействии с веществом, действия света вызывают колебания электрического вектора Е, поэтому его называют световым вектором.

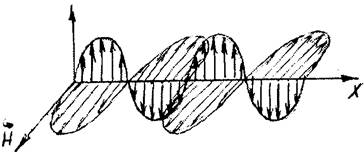
Рис. 1

В так называемом естественном свейте (свете, испускаемом обычными источниками) имеются колебания, совершающиеся в самых различных направлениях (плоскостях), перпендикулярных к лучу (рис.2а и 2б).

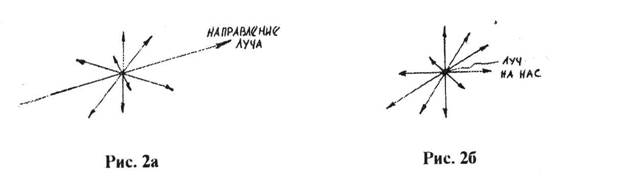
Плоскость колебаний для каждого вектора ориентирована здесь случайным образом. Поэтому в результирующей волне колебания различных направлений представлены с равной вероятностью. В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Поляризованным называется свет, в котором направления колебаний светового вектора упорядочены каким-либо образом.

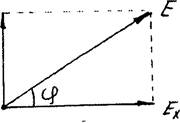
Рис. 3

Представим луч в виде двух взаимно перпендикулярных электрических колебаний (рис. 3). Результирующая напряженность Е является векторной суммой напряженностей Е_х и Е_у.. Угол j между направлениями векторов Е_х и Е_у. определяется выражением: .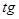

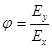Если разность фаз (определяется длинной векторов) претерпевает случайные хаотические изменения, то и угол j, т.е. положение светового вектора Е, будет испытывать скачкообразные неупорядоченные изменения. В соответствии с этим естественный свет можно представить в виде двух некогерентных электромагнитных волн, поляризованных во взаимно перпендикулярных плоскостях и имеющих одинаковую интенсивность. Такое представление намного упрощает рассмотрение прохождения естественного света через поляризованные устройства.

Если колебания светового вектора происходят только в одной проходящей через луч плоскости, свет называется плоско-поляризованным (или линейно поляризованным). В этом случае разность фаз между Е_х и Е_у равна 0 или pи результирующее колебание совершается в фиксированном направлении.

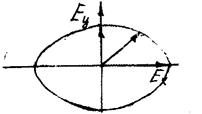
Рис.4

Упорядоченность может заключаться и в том, что вектор Е поворачивается (вращается) с частотой света вокруг луча, одновременно пульсируя по величине (рис. 4). Из учения о колебаниях известно, что два взаимно перпендикулярных гармонических колебания одинаковой частоты при сложении дают в общем случае движения по эллипсу, т.е. получается эллиптическая поляризованная волна. В частном случае получается движение по прямой (рассмотрено выше) и движение по окружности - свет называется поляризованным по кругу. Наиболее распространенный в практике поляризованный свет можно получить из естественного с помощью различных приборов, в частности, используют анизотропные кристаллы (призмы Никеля, Фуко, дихроичные пластинки и пленки и т.п.).

Эти приборы свободно пропускают колебания параллельные определенной плоскости кристалла и, наоборот, полностью задерживают колебания, перпендикулярные этой плоскости.

Закон Малюса.

Закон Малюса устанавливает зависимость между интенсивностью поляризованного света, прошедшего через анализатор и углом а между плоскостью колебаний света, падающего на анализатор, и плоскостью пропускания анализатора:

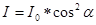(1)

При этом не учитывается отражение и поглощение света веществом анализатора. Теоретически закон Малюса основывается па разложении одной плоско поляризованной волны на две другие плоско поляризованные волны со взаимно перпендикулярными плоскостями колебаний. На рис. 5 поляризатор П падает плоско поляризованный свете амплитудой E_n. Анализатор пропускает колебания, совпадающие с направлением АА₀. Угол между плоскостями пропускания поляризатора и анализатора равен a. Разложим вектор Е_n на Е_А, совпадающий с направлением АА₀ и Е, перпендикулярный направлению АА₀..

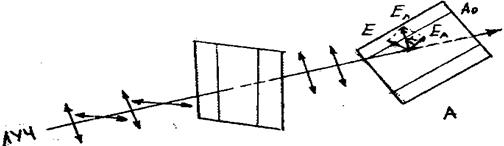
Рис. 5

Свет с амплитудой Е погасится анализатором, а с амплитудой Е_А пройдет через него. Из треугольника видно, что: E_А = E_n cos a (2)

Но глаз и фотоэлемент реагируют не на амплитуду колебаний, а на величину энергии, приносимой световой волной. Из теории колебаний известно, что величина энергии, приносимая волной, пропорциональна квадрату амплитуды, т.е.: W~E².

Используя понятие интенсивности как меры энергии, приносимой волной за единицу времени на единицу площади, можно говорить, что и интенсивность света пропорциональна квадрату амплитуды напряженности электрического вектора, т.е. I~Е².

Возведя равенство (2) в квадрат и заменив квадраты амплитуд Е_А² и Е_n² соответствующими интенсивностями I и I₀, получим закон Малюса.

Закон Брюстера.

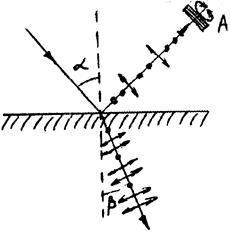
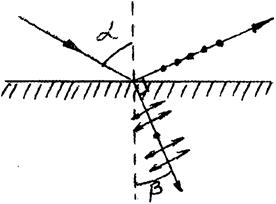
Рис. 7 Рис. 8

Установлено, что при отражении света от диэлектриков (например, стеклянной пластинки), если угол падения отличен от 0, отраженный и преломленный лучи оказываются частично поляризованными. В отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 7 они обозначены точками) в преломленном луче - колебания, параллельные плоскости падения (обозначены двухсторонними стрелками). Если такой частично поляризованный свет пропустить через анализатор А, то при вращении его вокруг направленного луча, интенсивность прошедшего света будет изменяться в пределах от I_max до I_min. За степень поляризации принимают соотношение:

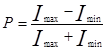
Так для плоско поляризованного света I_min = 0 (свет гасится полностью) и Р=1. В случае естественного света интенсивность его при поворочу анализатора меняться не будет, т.е I_max = I_min и тогда Р=0.

Опыт показывает, что степень поляризации при отражении и преломлении зависит oт угла падения: при некотором угле, называемом углом Брюстера, происходит полная поляризация отраженного луча (Р=1) - он содержит только колебания, перпендикулярные к плоскости падения. Что касается преломленного луча, то при угле падения Брюстера степень поляризации достигает наибольшего значения, однако этот луч остается поляризованным только частично (0<Р<1).

Угол Брюстера определяется из просто выражения: tg y =h₂₁ (4),

получившего название закона Брюстера. (h₂₁ - показатель преломления второй среды относительно первой).

При падении света под углом Брюстера отраженный и преломленный лучи оказываются взаимно перпендикулярными (рис. 8). Степень поляризации отраженного и преломленного лучей при различных углах падения можно вычислить с помощью формул Френеля, которые позволяют определить интенсивности.

При отражении естественного света от диэлектрической поверхности:

I(перпен)=0,5Io{sin(a-b)/sin(a+b)}^2

I(парал)=0.5Io{tg(a-b)/ tg(a+b)}^2,

где:

I(перпен)— интенсивность световых колебаний, совершающихся в направлении перпендикулярном к плоскости падения света;

I(парал)- интенсивность световых колебаний, совершающихся в направлении параллельном плоскости падения;

Io - интенсивность падающего естественного света.

Упражнение № 1.

Экспериментальна проверка закона Малюса

Экспериментальна проверка закона Малюса, производится с помощью установки изображенной на рис.6. От источника света S свет проходит через диафрагму Д, объектив О, поляроиды П и А и попадает на фотоэлемент ФЭ. Возникающий фототок регистрируется гальванометром Г. Получив четкое изображение диафрагмы на фотоэлементе, устанавливают показатель поворота анализатора на отметку 90⁰. Приняв меры к предотвращению попадания постороннего света на фотоэлемент, поворачивают поляризатор, добиваясь наименьшего отклонения стрелки гальванометра, такое положение соответствует "скрещенным" поляроидам, т.e. угол a равен 90° (положение указателя поворота поляризатора П, при этом должно быть равно "0"" или "180°"). Не меняя положения поляризатора, изменяют угол a вращая анализатор в пределах от 0° до 180° через 10°. При этом записывают показания гальванометра (таблица 1). Считая величину фототока пропорциональной интенсивности света, падающего на фотоэлемент, построить график зависимости интенсивности I от угла a между плоскостями пропускания поляризатора и анализатора, а затем график зависимости I от cos a. Для более строгой проверки зависимости I от a следует вычислить значения cos² a для соответствующих углов и построить на миллиметровой бумаге 10х15 см график зависимости I от cos² a. В этом случае экспериментальные точки должны укладываться на прямой линии.

Упражнение № 2.